3 D Computater Vision CSc 83020 Revisit filtering

3 -D Computater Vision CSc 83020 § Revisit filtering (Gaussian and Median) § Introduction to edge detection 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Linear Filters § Given an image In(x, y) generate a new image Out(x, y): § For each pixel (x, y) Out(x, y) is a linear combination of pixels in the neighborhood of In(x, y) § This algorithm is § Linear in input intensity § Shift invariant 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Discrete Convolution § This is the discrete analogue of convolution § The pattern of weights is called the “kernel” of the filter § Will be useful in smoothing, edge detection 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Computing Convolutions § What happens near edges of image? § Ignore (Out is smaller than In) § Pad with zeros (edges get dark) § Replicate edge pixels § Wrap around § Reflect § Change filter 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Example: Smoothing Original: Mandrill Smoothed with Gaussian kernel 3 -D Computer Vision CSc 83020 / Ioannis Stamos

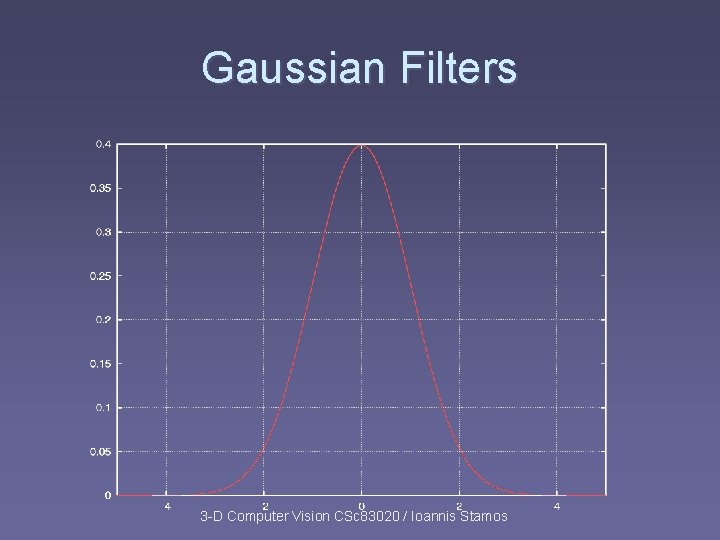
Gaussian Filters § One-dimensional Gaussian § Two-dimensional Gaussian 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Gaussian Filters 3 -D Computer Vision CSc 83020 / Ioannis Stamos

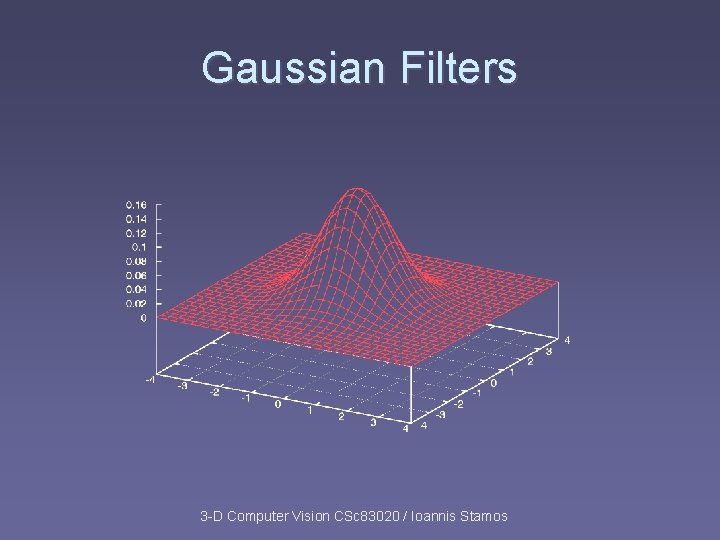
Gaussian Filters 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Gaussian Filters § Gaussians are used because: § Smooth § Decay to zero rapidly § Simple analytic formula § Limit of applying multiple filters is Gaussian (Central limit theorem) § Separable: G 2(x, y) = G 1(x) G 1(y) 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Size of the mask 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Edges & Edge Detection § What are Edges? § Theory of Edge Detection. § Edge Operators (Convolution Masks) § Edge Detection in the Brain? § Edge Detection using Resolution Pyramids 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Edges 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What are Edges? Rapid Changes of intensity in small region 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What are Edges? Surface-Normal discontinuity Depth discontinuity Surface-Reflectance Discontinuity Illumination Discontinuity Rapid Changes of intensity in small region 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Local Edge Detection 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What is an Edge? Edge easy to find 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What is an Edge? Where is edge? Single pixel wide or multiple pixels? 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What is an Edge? Noise: have to distinguish noise from actual edge 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What is an Edge? Is this one edge or two? 3 -D Computer Vision CSc 83020 / Ioannis Stamos

What is an Edge? Texture discontinuity 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Local Edge Detection 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Edge Types Ideal Step Edges Ideal Ridge Edges Ideal Roof Edges 3 -D Computer Vision CSc 83020 / Ioannis Stamos

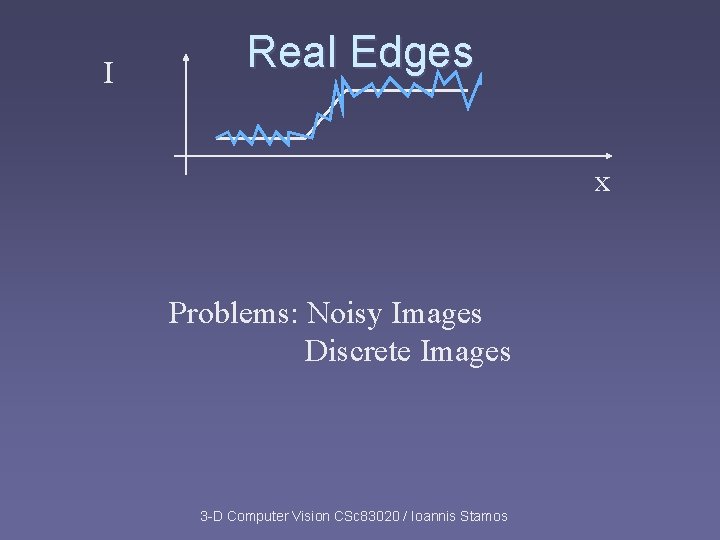
I Real Edges x Problems: Noisy Images Discrete Images 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Real Edges We want an Edge Operator that produces: Edge Magnitude (strength) Edge direction Edge normal Edge position/center High detection rate & good localization 3 -D Computer Vision CSc 83020 / Ioannis Stamos

The 3 steps of Edge Detection § Noise smoothing § Edge Enhancement § Edge Localization § Nonmaximum suppression § Thresholding 3 -D Computer Vision CSc 83020 / Ioannis Stamos

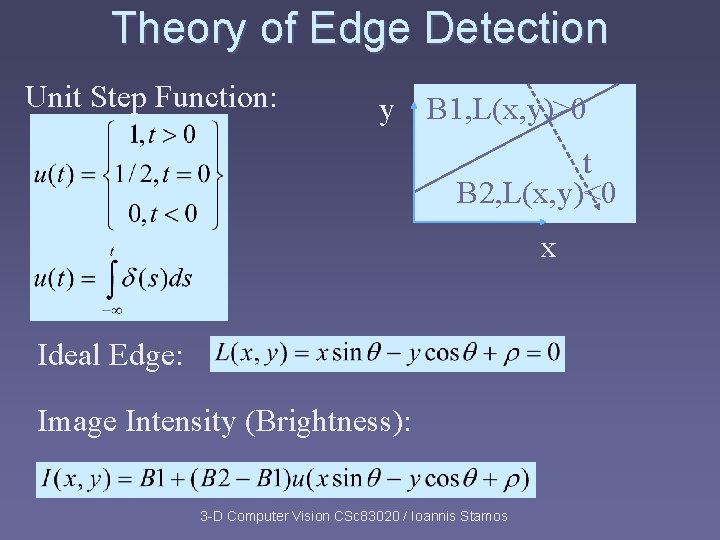
Theory of Edge Detection Unit Step Function: y B 1, L(x, y)>0 t B 2, L(x, y)<0 x 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Theory of Edge Detection Unit Step Function: y B 1, L(x, y)>0 t B 2, L(x, y)<0 x Ideal Edge: Image Intensity (Brightness): 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Theory of Edge Detection Partial Derivatives: y B 1, L(x, y)>0 t B 2, L(x, y)<0 Directional! x 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Theory of Edge Detection y B 1, L(x, y)>0 t B 2, L(x, y)<0 Squared Gradient: Edge Magnitude Edge Orientation Rotationally 3 -DSymmetric, Non-Linear Computer Vision CSc 83020 / Ioannis Stamos x

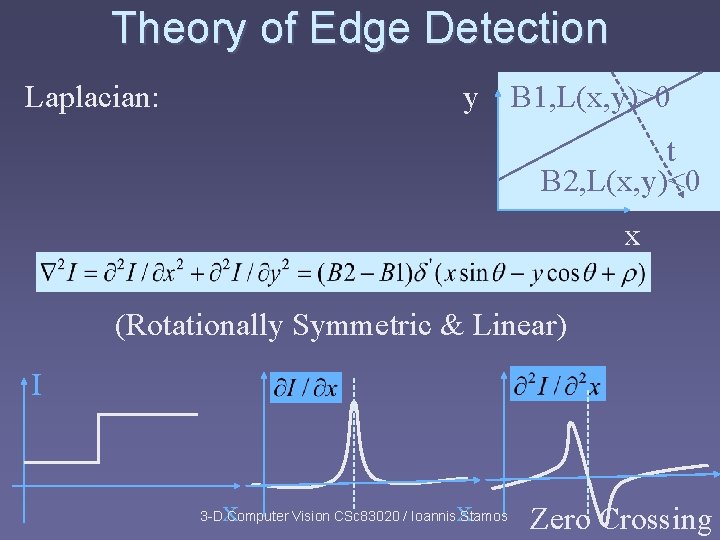
Theory of Edge Detection Laplacian: y B 1, L(x, y)>0 t B 2, L(x, y)<0 x (Rotationally Symmetric & Linear) I x x 3 -D Computer Vision CSc 83020 / Ioannis Stamos Zero Crossing

Difference Operators Ii, j+1 Ii+1, j+1 ε Ii, j Ii+1, j Finite Difference Approximations 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Squared Gradient y x 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Squared Gradient [Roberts ’ 65] if threshold then we have an edge 3 -D Computer Vision CSc 83020 / Ioannis Stamos

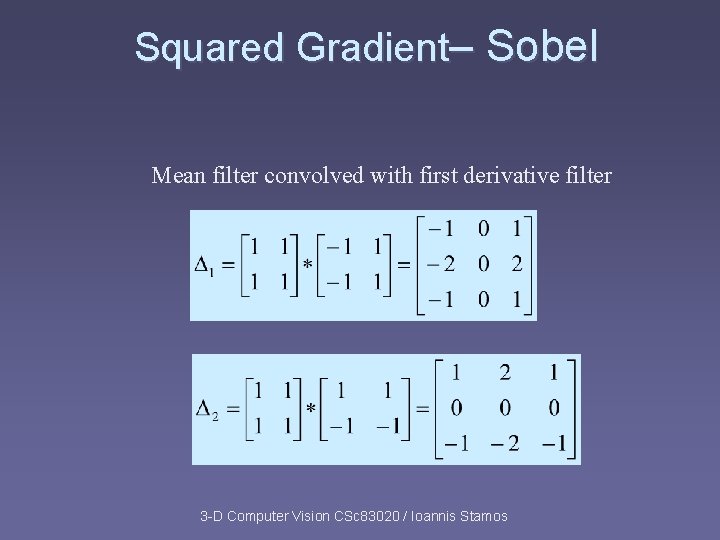
Squared Gradient– Sobel Mean filter convolved with first derivative filter 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Examples First derivative Sobel operator 3 -D Computer Vision CSc 83020 / Ioannis Stamos

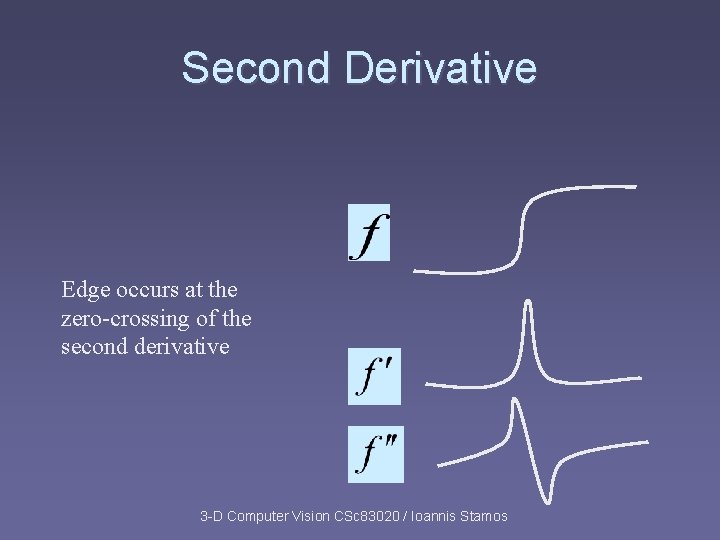
Second Derivative Edge occurs at the zero-crossing of the second derivative 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Laplacian • Rotationally symmetric • Linear computation (convolution) 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Discrete Laplacian Ii-1, j+1 Ii+1, j+1 Ii-1, j-1 Ii, j Ii+1, j Ii, j-1 Ii+1, j-1 Finite Difference Approximations 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Discrete Laplacian More accurate • Rotationally symmetric • Linear computation (convolution) 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Discrete Laplacian of an image 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Discrete Laplacian is sensitive to noise First smooth image with Gaussian 3 -D Computer Vision CSc 83020 / Ioannis Stamos

From Forsyth & Ponce. 3 -D Computer Vision CSc 83020 / Ioannis Stamos

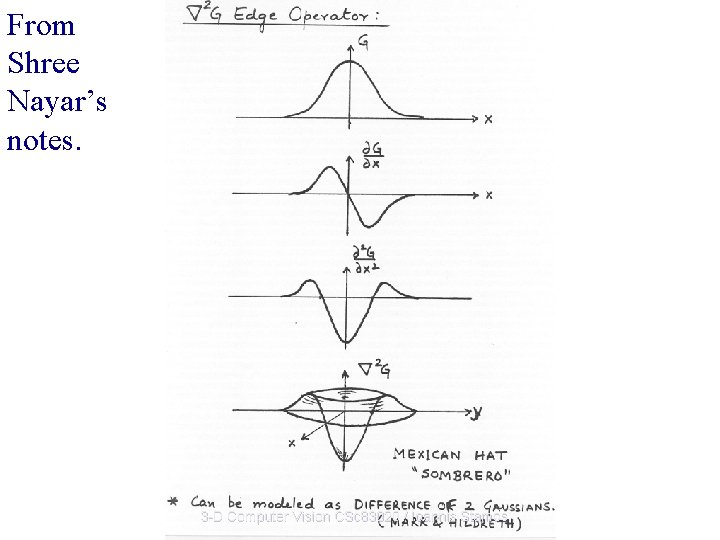
From Shree Nayar’s notes. 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Discrete Laplacian w/ Smoothing 3 -D Computer Vision CSc 83020 / Ioannis Stamos

From Shree Nayar’s notes. 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Difference Operators – Second Derivative 3 -D Computer Vision CSc 83020 / Ioannis Stamos

From Forsyth & Ponce. 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Edge Detection – Human Vision Lo. G convolution in the brain – biological evidence! Flipped Lo. G 3 -D Computer Vision CSc 83020 / Ioannis Stamos

Image Resolution Pyramids Can save computations. Consolidation: Average pixels at one level to find value at higher level. Template Matching: Find match in COARSE resolution 3 -D Computer Vision CSc 83020 / Ioannis Stamos Then move to FINER resolution.

From Forsyth & Ponce. 3 -D Computer Vision CSc 83020 / Ioannis Stamos