3 D angular momentum and isospin restored calculations

3 D angular momentum and isospin restored calculations with the Skyrme EDF Wojciech Satuła in collaboration with J. Dobaczewski, W. Nazarewicz & M. Rafalski Intro: define fundaments my model is „standing on” sp mean-field (or nuclear DFT) beyond mean-field (projection after variation) Symmetry (isospin) violation and restoration: unphysical symmetry violation isospin projection Coulomb rediagonalization (explicit symmetry violation) Results isospin impurities in ground-states of e-e nuclei structural effects SD bands in 56 Ni ISB corrections to superallowed beta decay Summary ab initio + NNN +. . tens of Me. V

Skyrme-force-inspired local energy density functional (without pairing) Y | v(1, 2) | Y average Skyrme interaction (in fact a functional!) over the Slater determinant local energy density functional SV is the only Skyrme interaction Beiner et al. NPA 238, 29 (1975) Skyrme (nuclear) interaction conserves: rotational (spherical) symmetry LS isospin symmetry: Vnn = Vpp. LS= Vnp. LS (in reality approximate) Mean-field solutions (Slater determinants) break (spontaneously) these symmetries Total energy (a. u. ) Symmetry-conserving configurtion Symmetry-breaking configurations Deformation (q)

Restoration of broken symmetry Beyond mean-field multi-reference density functional theory rotated Slater determinants are equivalent solutions Euler angles gauge angle in space or/and isospace where

Isospin symmetry restoration There are two sources of the isospin symmetry breaking: Engelbrecht & Lemmer, - unphysical, unphysical caused solely by the HF approximation PRL 24, (1970) 607 - physical, caused mostly by Coulomb interaction physical (also, but to much lesser extent, by the strong force isospin non-invariance) Find self-consistent HF solution (including Coulomb) deformed Slater determinant |HF>: See: Caurier, Poves & Zucker, PL 96 B, (1980) 11; 15 Apply the isospin projector: a. CBR = 1 - |b. T=|Tz||2 in order to create good isospin „basis”: Diagonalize total Hamiltonian in „good isospin basis” |a, T, Tz> takes physical isospin mixing AR n=1 2 a. C = 1 - |a. T=T | z

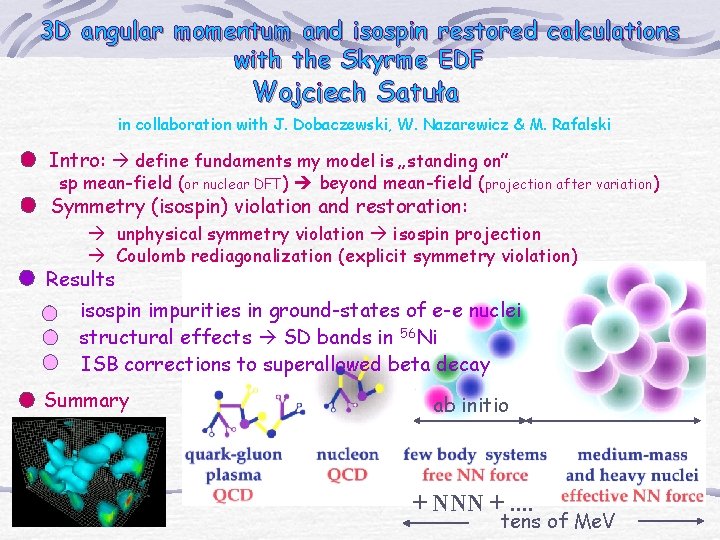
Numerical results: (I) Isospin impurities in ground states of e-e nuclei W. Satuła, J. Dobaczewski, W. Nazarewicz, M. Rafalski, PRL 103 (2009) 012502 Ca isotopes: BR SLy 4 AR 0. 4 Here the HF is solved without Coulomb |HF; e. MF=0>. a. C [%] 0. 2 Here the HF is solved with Coulomb |HF; e. MF=e>. e. MF = 0 0 1 0. 8 0. 01 0. 6 40 0. 4 44 48 52 56 60 e. MF = e 0. 2 In both cases rediagonalization is performed for the total Hamiltonian including Coulomb 0 40 44 56 48 52 Mass number A 60

E-EHF [Me. V] a. C [%] (II) Isospin mixing & energy in the ground states of e-e N=Z nuclei: 6 5 4 3 2 1 0 1. 0 0. 8 0. 6 0. 4 0. 2 0 N=Z nuclei AR BR BR SLy 4 BR AR HF tries to reduce the isospin mixing by: Da. C ~30% in order to minimize the total energy Projection increases the ground state energy (the Coulomb and symmetry energies are repulsive) Rediagonalization (GCM) AR 20 28 36 44 52 60 68 76 84 92 100 A lowers the ground state energy but only slightly below the HF This is not a single Slater determinat There are no constraints on mixing coefficients

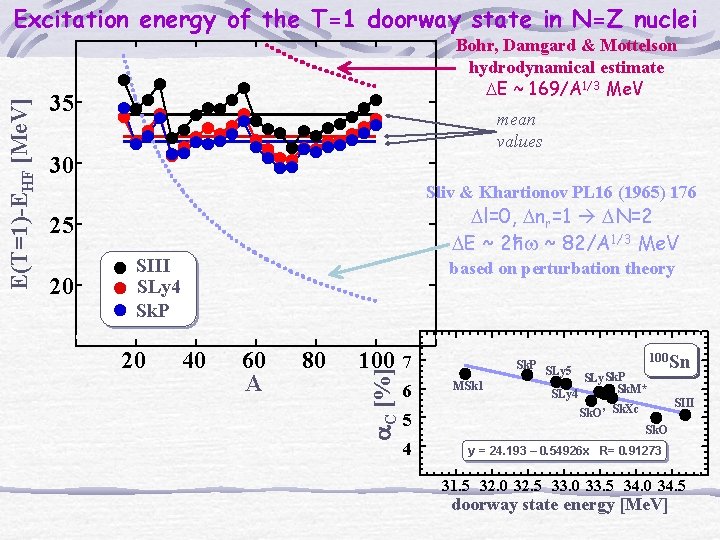
Bohr, Damgard & Mottelson hydrodynamical estimate DE ~ 169/A 1/3 Me. V 35 mean values 30 Sliv & Khartionov PL 16 (1965) 176 Dl=0, Dnr=1 DN=2 DE ~ 2 hw ~ 82/A 1/3 Me. V 25 20 SIII SLy 4 Sk. P 20 based on perturbation theory 40 60 A 80 100 a. C [%] E(T=1)-EHF [Me. V] Excitation energy of the T=1 doorway state in N=Z nuclei 7 6 5 4 Sk. P MSk 1 SLy 5 SLy. Sk. P Sk. M* SLy 4 Sk. O’ Sk. Xc 100 Sn SIII Sk. O y = 24. 193 – 0. 54926 x R= 0. 91273 31. 5 32. 0 32. 5 33. 0 33. 5 34. 0 34. 5 doorway state energy [Me. V]

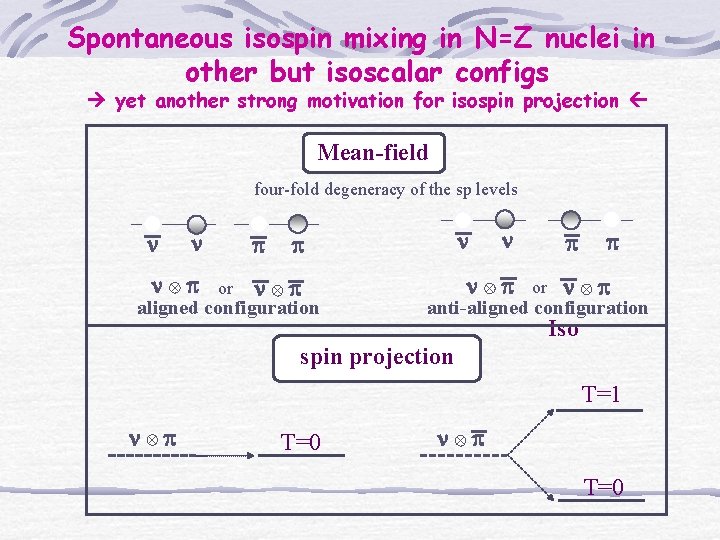
Spontaneous isospin mixing in N=Z nuclei in other but isoscalar configs yet another strong motivation for isospin projection Mean-field four-fold degeneracy of the sp levels n n n p p or n p aligned configuration n n p p or p n p anti-aligned configuration Iso spin projection T=1 n p T=0

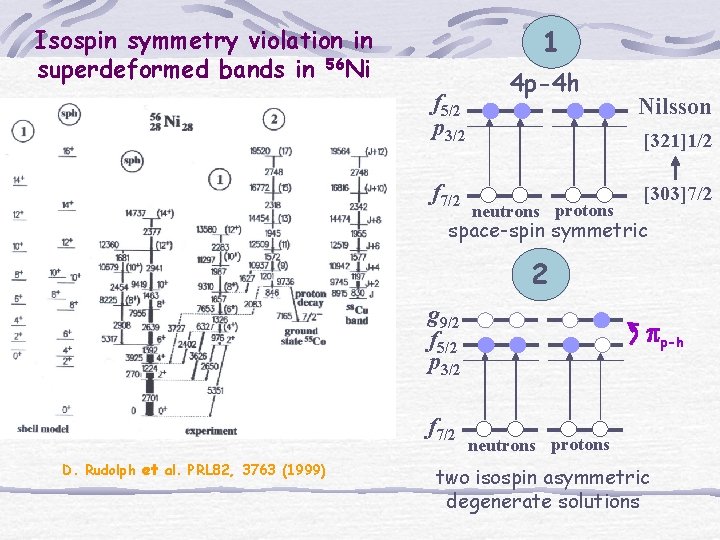
1 Isospin symmetry violation in superdeformed bands in 56 Ni f 5/2 p 3/2 f 7/2 4 p-4 h Nilsson [321]1/2 neutrons protons [303]7/2 space-spin symmetric 2 g 9/2 f 5/2 p 3/2 f 7/2 D. Rudolph et al. PRL 82, 3763 (1999) pp-h neutrons protons two isospin asymmetric degenerate solutions

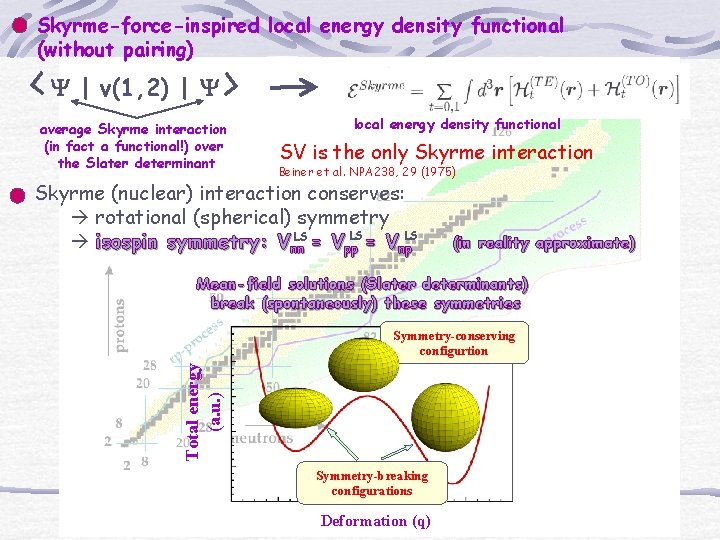
Isospin projection Mean-field T=1 d. ET Excitation energy [Me. V] pph 20 centroid a. C [%] nph d. ET T=0 8 6 4 2 band 1 Isospin-projection Hartree-Fock 16 56 Ni 12 Exp. band 1 Exp. band 2 Th. band 1 Th. band 2 8 4 5 10 15 Angular momentum W. Satuła, J. Dobaczewski, W. Nazarewicz, M. Rafalski, PRC 81 (2010) 054310

Isospin-projection is non-singular: W. Satuła, J. Dobaczewski, W. Nazarewicz, M. Rafalski, PRC 81 (2010) 054310 SVD eigenvalues (diagonal matrix) SVD singularity (if any) at b=p is inherited by r r~ =S yi* Oij-1 jj ij 1 + |N-Z| - h + |N-Z|+2 k in the worst case k is a multiplicity of zero singular values h> 3

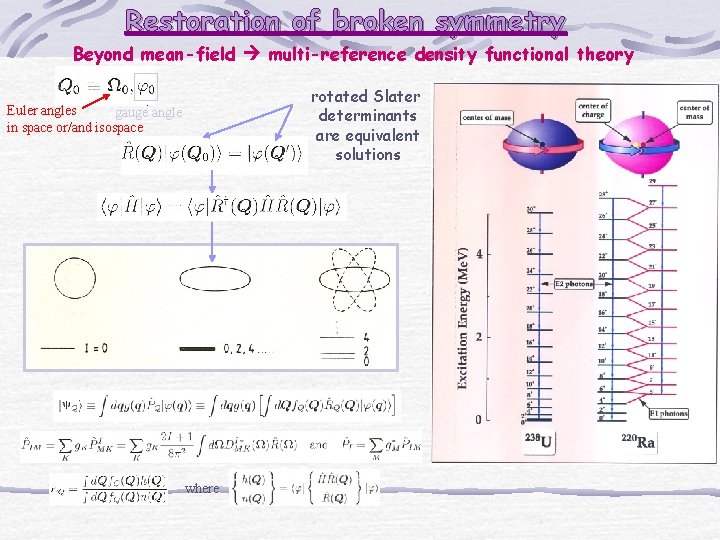
42 Sc – isospin projection from [K, -K] configurations with K=1/2, …, 7/2 isospin & angular momentum 40 a. C [%] isospin 30 20 10 0. 586(2)% 0 1 3 2 K 5 7 Isospin and angular-momentum projected DFT is ill-defined except for the hamiltonian-driven functionals there is no alternative but Skyrme SV

Why we have to to use Skyrme-V? |OVERLAP| 1 0. 1 only IP 0. 01 0. 0001 IP+AMP 0. 0 0. 5 1. 0 1. 5 2. 0 r =S yi* Oij jj T -1 2. 5 3. 0 b. T [rad] p ij HF sp state inverse of the overlap matrix space & isospin rotated sp state

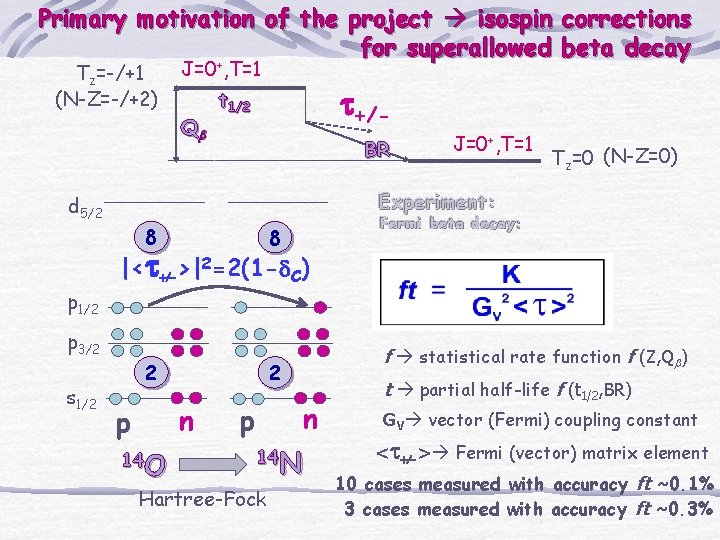
Primary motivation of the project isospin corrections for superallowed beta decay Tz=-/+1 (N-Z=-/+2) J=0+, T=1 Qb t+/- t 1/2 BR 8 Fermi beta decay: 8 |<t+/->|2=2(1 -d. C) p 3/2 s 1/2 Tz=0 (N-Z=0) Experiment: d 5/2 p 1/2 J=0+, T=1 2 2 n p 14 O f statistical rate function f (Z, Qb) n p 14 N Hartree-Fock t partial half-life f (t 1/2, BR) GV vector (Fermi) coupling constant <t+/-> Fermi (vector) matrix element 10 cases measured with accuracy ft ~0. 1% 3 cases measured with accuracy ft ~0. 3%

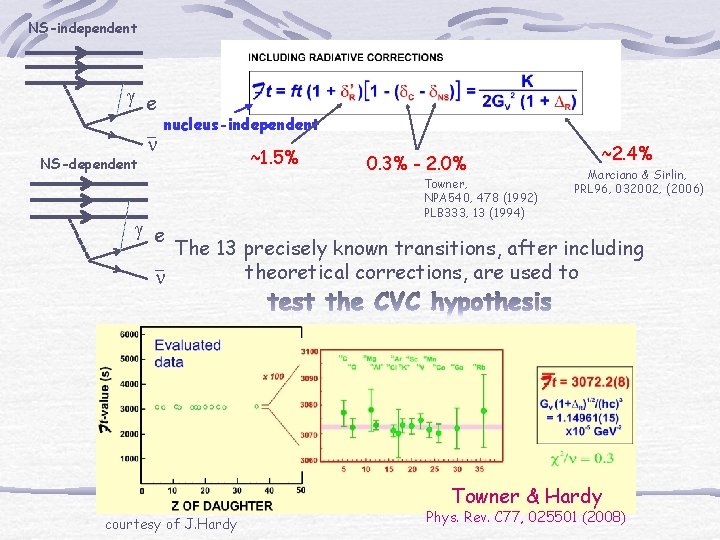
NS-independent g e NS-dependent n nucleus-independent g e ~1. 5% 0. 3% - 2. 0% Towner, NPA 540, 478 (1992) PLB 333, 13 (1994) ~2. 4% Marciano & Sirlin, PRL 96, 032002, (2006) The 13 precisely known transitions, after including theoretical corrections, are used to n Towner & Hardy courtesy of J. Hardy Phys. Rev. C 77, 025501 (2008)

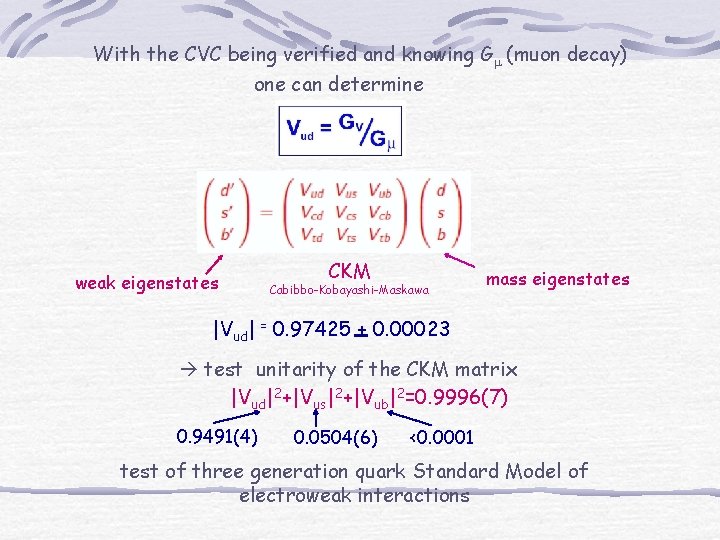
With the CVC being verified and knowing Gm (muon decay) one can determine weak eigenstates CKM Cabibbo-Kobayashi-Maskawa mass eigenstates |Vud| = 0. 97425 + 0. 00023 test unitarity of the CKM matrix |Vud|2+|Vus|2+|Vub|2=0. 9996(7) 0. 9491(4) 0. 0504(6) <0. 0001 test of three generation quark Standard Model of electroweak interactions

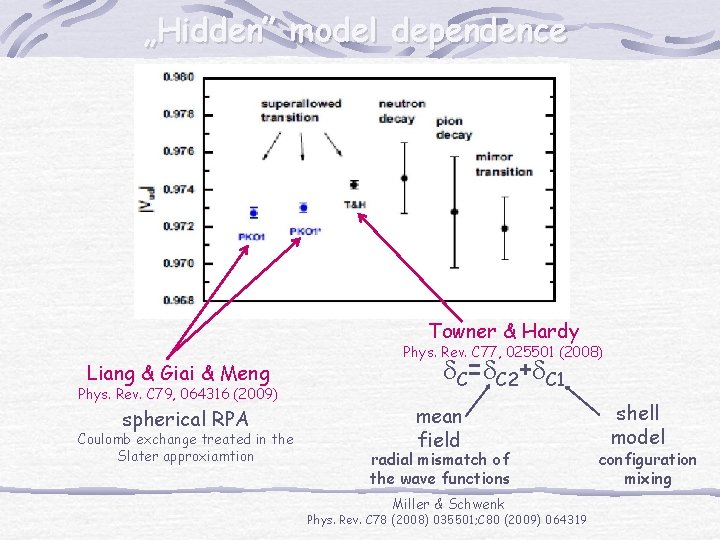
„Hidden” model dependence Towner & Hardy Liang & Giai & Meng Phys. Rev. C 79, 064316 (2009) spherical RPA Coulomb exchange treated in the Slater approxiamtion Phys. Rev. C 77, 025501 (2008) d. C=d. C 2+d. C 1 mean field radial mismatch of the wave functions Miller & Schwenk Phys. Rev. C 78 (2008) 035501; C 80 (2009) 064319 shell model configuration mixing

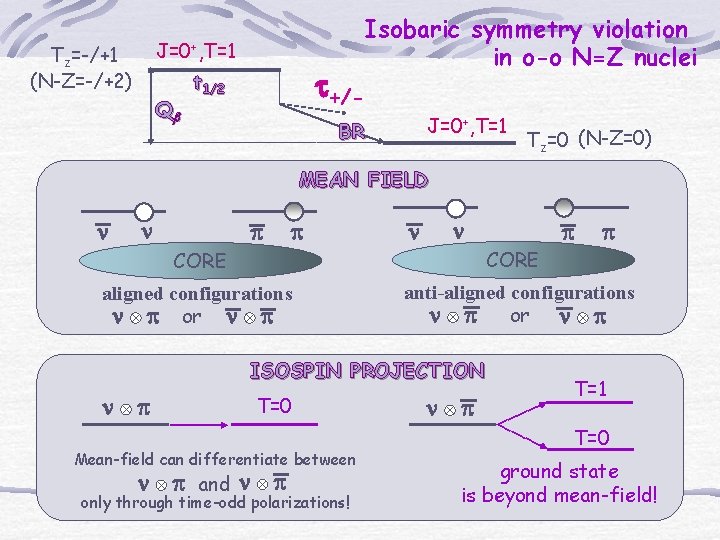
J=0+, T=1 Tz=-/+1 (N-Z=-/+2) Qb t+/- t 1/2 Isobaric symmetry violation in o-o N=Z nuclei J=0+, T=1 BR Tz=0 (N-Z=0) MEAN FIELD n n p p n n CORE aligned configurations n p or n p T=0 Mean-field can differentiate between n p and n p only through time-odd polarizations! p anti-aligned configurations n p or n p ISOSPIN PROJECTION n p p n p T=1 T=0 ground state is beyond mean-field!

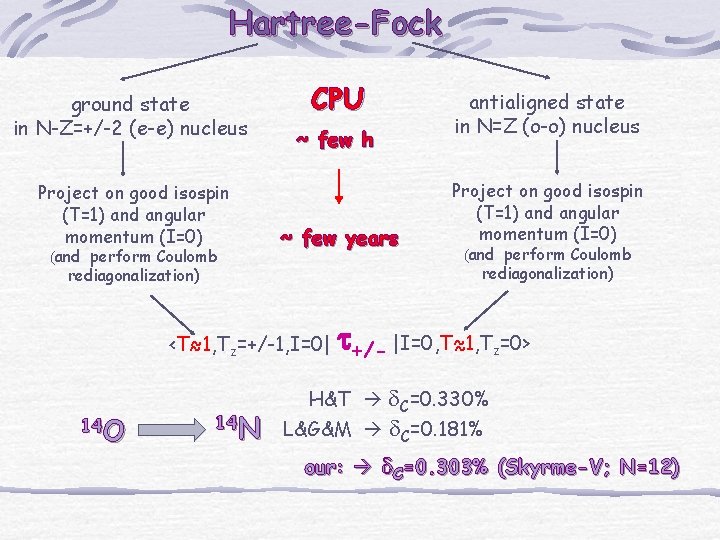
Hartree-Fock ground state in N-Z=+/-2 (e-e) nucleus Project on good isospin (T=1) and angular momentum (I=0) (and perform Coulomb CPU antialigned state in N=Z (o-o) nucleus ~ few h ~ few years Project on good isospin (T=1) and angular momentum (I=0) (and perform Coulomb rediagonalization) t <T~1, T ~ z=0> ~ z=+/-1, I=0| +/- |I=0, T~1, T 14 O 14 N H&T d. C=0. 330% L&G&M d. C=0. 181% our: d. C=0. 303% (Skyrme-V; N=12)

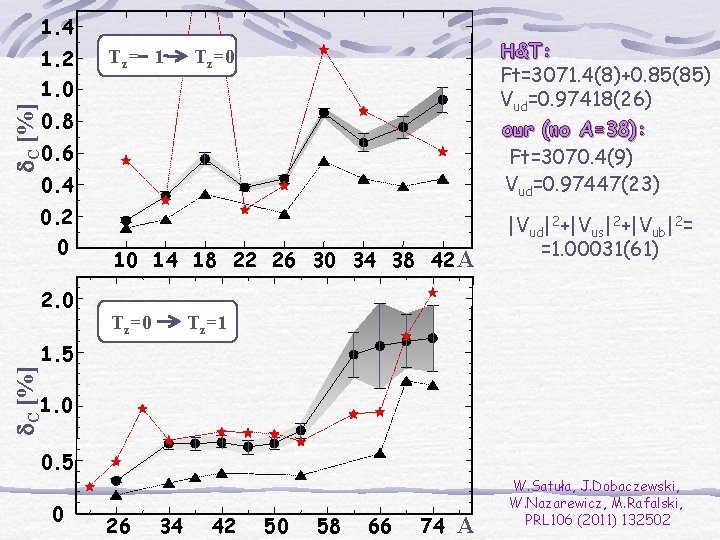
1. 4 1. 2 Tz = 1 H&T: Ft=3071. 4(8)+0. 85(85) Vud=0. 97418(26) our (no A=38): Ft=3070. 4(9) Vud=0. 97447(23) Tz=0 d. C [%] 1. 0 0. 8 0. 6 0. 4 0. 2 0 2. 0 10 14 18 22 26 30 34 38 42 A Tz=0 |Vud|2+|Vus|2+|Vub|2= =1. 00031(61) Tz=1 d. C [%] 1. 5 1. 0 0. 5 0 26 34 42 50 58 66 74 A W. Satuła, J. Dobaczewski, W. Nazarewicz, M. Rafalski, PRL 106 (2011) 132502

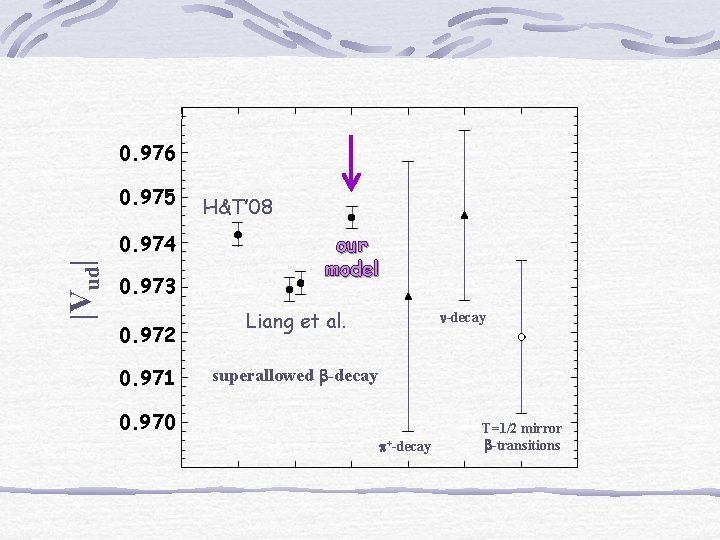
0. 976 0. 975 |Vud| 0. 974 0. 973 0. 972 0. 971 H&T’ 08 our model Liang et al. n-decay superallowed b-decay 0. 970 p+-decay T=1/2 mirror b-transitions

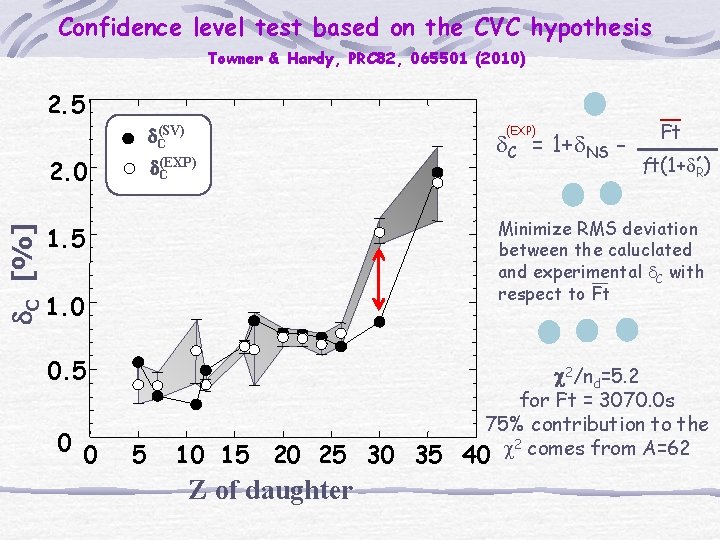
Confidence level test based on the CVC hypothesis Towner & Hardy, PRC 82, 065501 (2010) 2. 5 (EXP) d. C(SV) d. C [%] 2. 0 d. C (EXP) ‚ ft(1+d. R) Minimize RMS deviation between the caluclated and experimental d. C with respect to Ft 1. 5 1. 0 0. 5 0 0 d. C = 1+d. NS - Ft 5 10 15 20 25 30 35 Z of daughter c 2/nd=5. 2 for Ft = 3070. 0 s 75% contribution to the 2 40 c comes from A=62

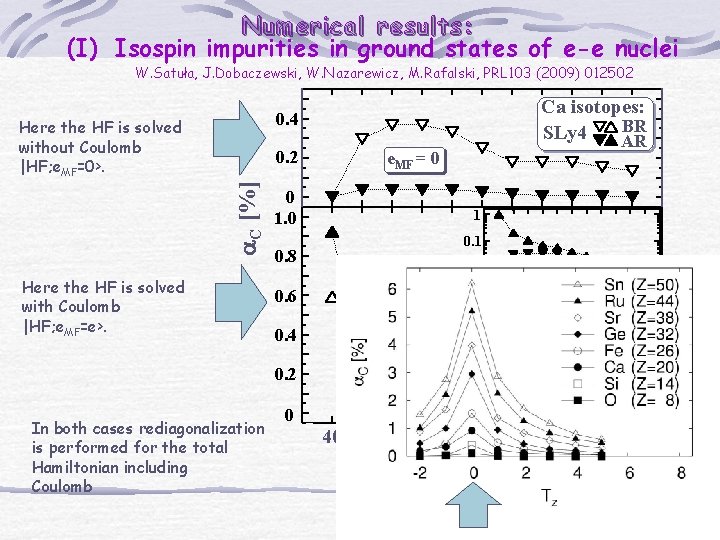
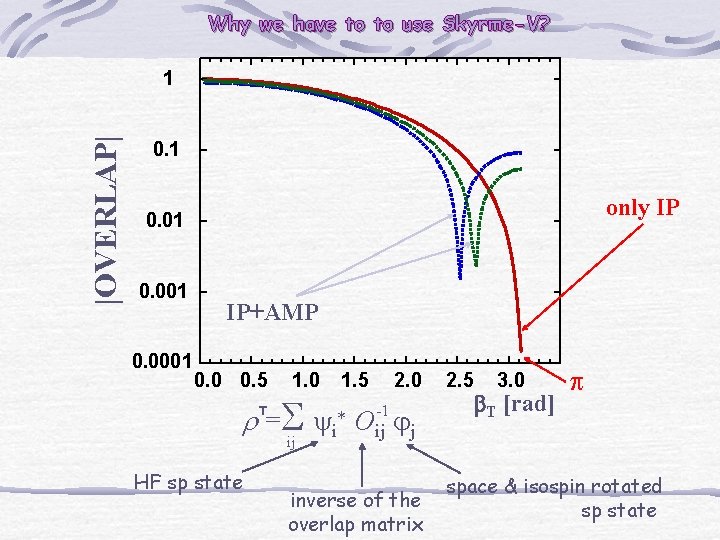
SUMMARY OF THE CALCULATIONS Ncutoff=12 Ncutoff=10 2. 5 Tz Tz+1 d. C [%] 2. 0 A=58 A=38 1. 5 1. 0 A=18 0. 5 0 0 Tz = -1 Tz = 0 10 20 30 40 A 50 60 70 80

Summary Elementary excitations in binary systems may differ from simple particle-hole (quasi-particle) exciatations especially when interaction among particles posseses additional symmetry (like the isospin symmetry in nuclei) Projection techniques seem to be necessary to account for those excitations - how to construct non-singular EDFs? [Isospin projection, unlike the angular-momentum and particle-number projections, is practically non-singular !!!] Superallowed 0+ 0+beta decay: encomaps extremely rich physics: CVC, Vud, unitarity of the CKM matrix, scalar currents… connecting nuclear and particle physics … there is still something to do in dc business … Pairing & other (shape vibrations) correlations can be „realtively easily” incorporated into the scheme by combining projection(s) with GCM

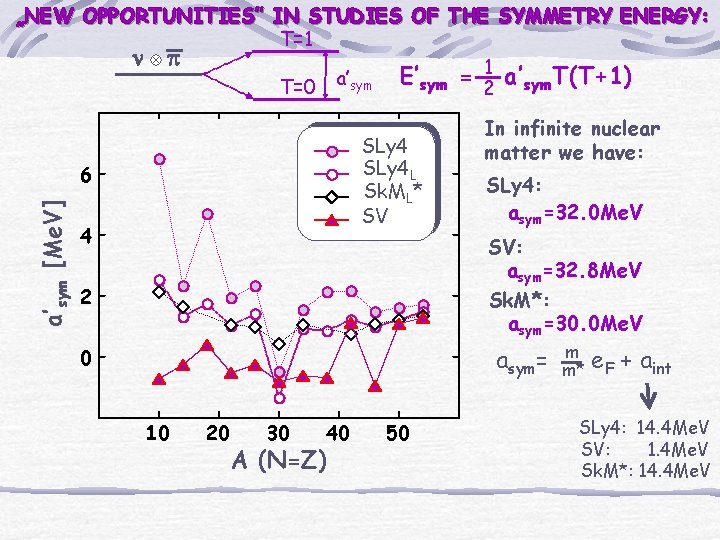
„NEW OPPORTUNITIES” IN STUDIES OF THE SYMMETRY ENERGY: T=1 n p 1 a’ T(T+1) E’ = a’ sym T=0 2 sym SLy 4 L Sk. ML* SV a’sym [Me. V] 6 4 In infinite nuclear matter we have: SLy 4: asym=32. 0 Me. V SV: asym=32. 8 Me. V 2 Sk. M*: asym=30. 0 Me. V asym= 0 10 20 30 40 A (N=Z) 50 m m* e. F + aint SLy 4: 14. 4 Me. V SV: 1. 4 Me. V Sk. M*: 14. 4 Me. V