3 Atomic Structure Overview Characteristics of Atoms Interaction

3 -Atomic Structure Overview • Characteristics of Atoms • Interaction b/tw matter and light – Photoelectric Effect • Absorption and Emission Spectra • Electron behavior • Quantum numbers

Atomic Structure • Atomic orbitals – Orbital energies – Electron configuration and the periodic table • Periodic table – Periodic properties – Energy

Characteristics of Atoms • • Atoms possess mass Atoms contain positive nuclei Atoms contain electrons Atoms occupy volume Atoms have various properties Atoms attract one another Atoms can combine with one another to form molecules

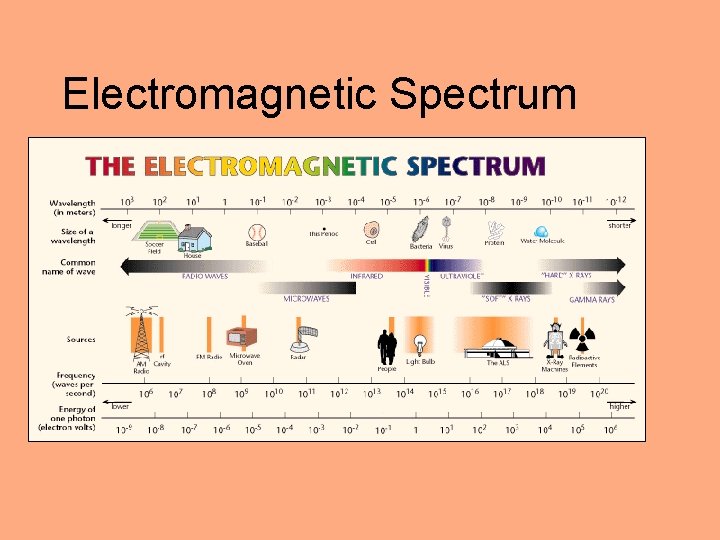
Atomic Structure • Atomic structure studied through atomic interaction with light • Light: electromagnetic radiation – carries energy through space – moves at 3. 00 x 108 m/s in vacuum – wavelike characteristics

Electromagnetic Spectrum

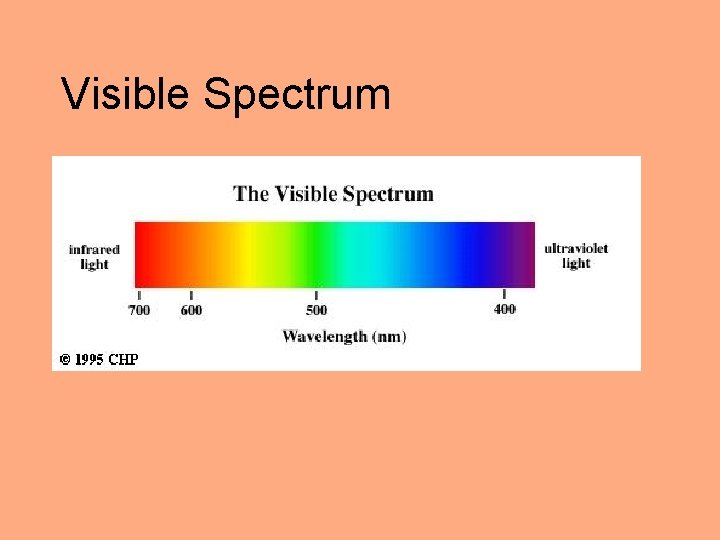
Visible Spectrum

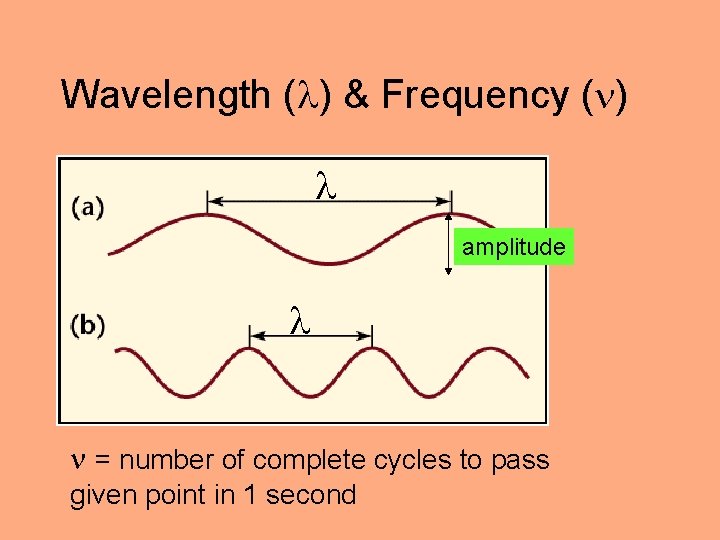
Wavelength ( ) & Frequency ( ) amplitude = number of complete cycles to pass given point in 1 second

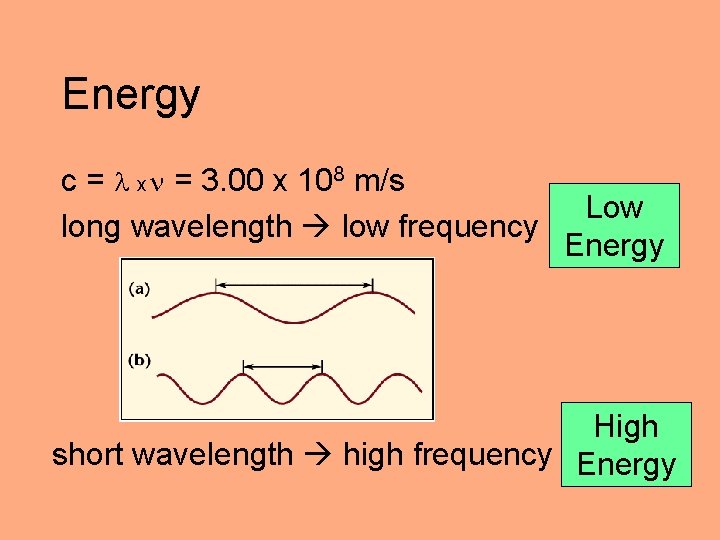
Energy c = x = 3. 00 x 108 m/s long wavelength low frequency Low Energy High short wavelength high frequency Energy

Energy Mathematical relationship: E = h E = energy h = Planck’s constant: 6. 63 x 10– 34 J s = frequency in s– 1

Energy Mathematical relationship: E = h c = x E= Energy: directly proportional to frequency inversely proportional to wavelength

Problems 3 -1, 2, & 3 1. a) Calculate the wavelength of light with a frequency = 5. 77 x 1014 s– 1 b) What is the energy of this light? 2. Which is higher in energy, light of wavelength of 250 nm or light of 5. 4 x 10– 7 m? 3. a) What is the frequency of light with an energy of 3. 4 x 10– 19 J? b) What is the wavelength of light with an energy of 1. 4 x 10– 20 J?

Photoelectric Effect • Light on metal surface • Electrons emitted • Threshold frequency, o If < o, no photoelectric effect If > o, photoelectric effect As , kinetic energy of electrons

Photoelectric Effect Einstein: energy frequency If < o electron doesn’t have enough energy to leave the atom If > o electron does have enough energy to leave the atom Energy is transferred from light to electron, extra is kinetic energy of electron Ephoton = h o + KEelectron = h photon – h o Animation

Problem 3 -4 A given metal has a photoelectric threshold frequency of o = 1. 3 x 1014 s 1. If light of = 455 nm is used to produce the photoelectric effect, determine the kinetic energy of the electrons that are produced.

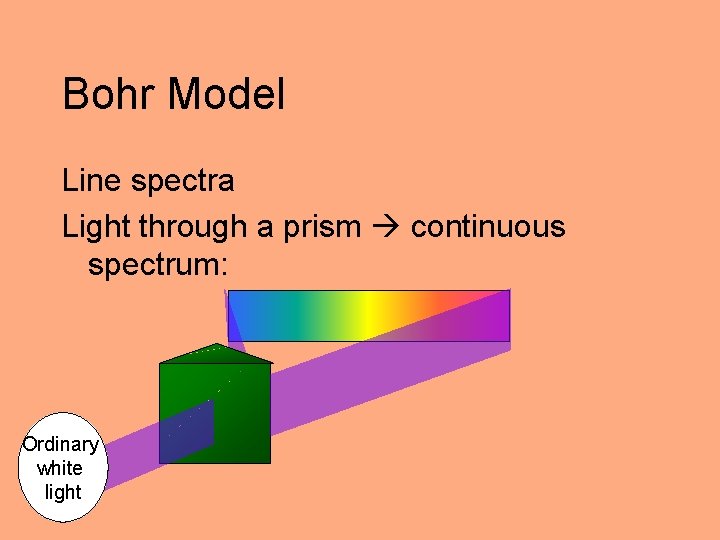
Bohr Model Line spectra Light through a prism continuous spectrum: Ordinary white light

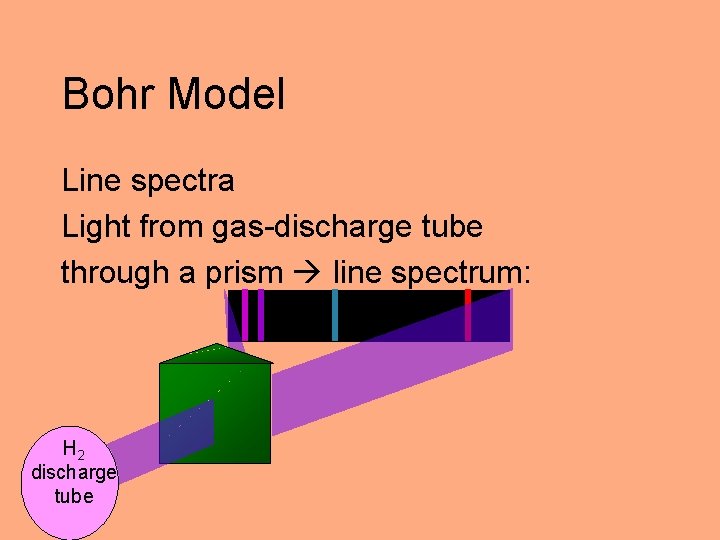
Bohr Model Line spectra Light from gas-discharge tube through a prism line spectrum: H 2 discharge tube

Line Spectra (emission) White light H He Ne

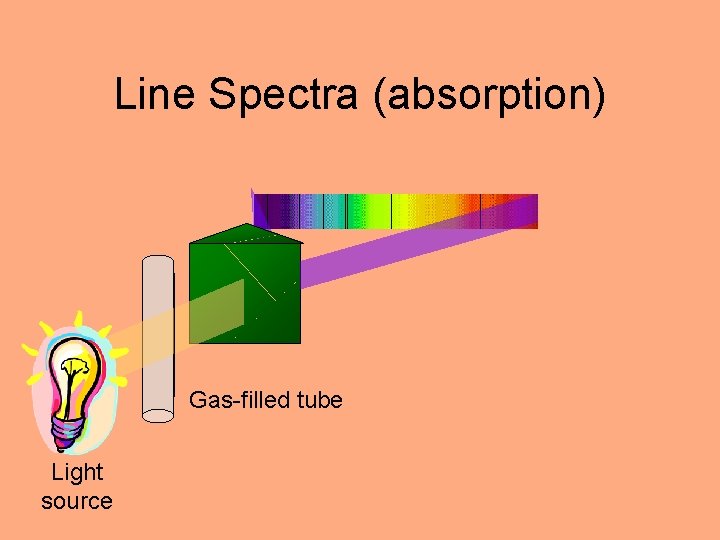
Line Spectra (absorption) Gas-filled tube Light source

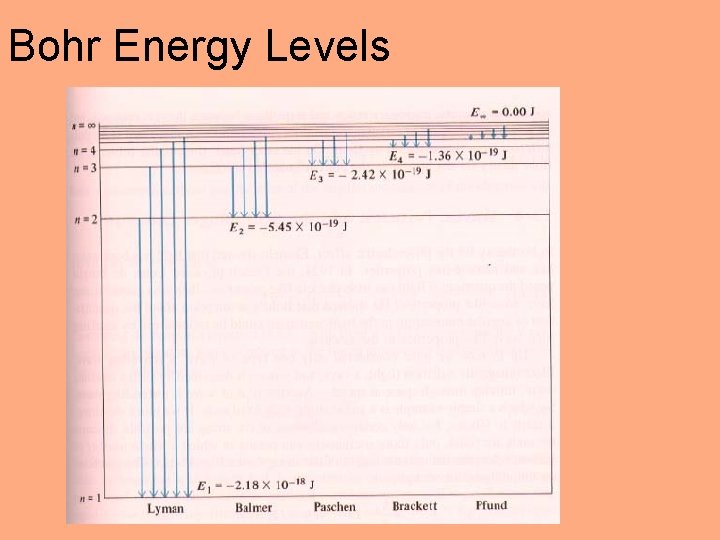
Bohr Model For hydrogen: C = 3. 29 x 1015 s– 1 Niels Bohr: Electron energy in the atom is quantized. n = 1, 2, 3, …. RH = 2. 18 x 10– 18 J

Bohr Model Eatom = Eelectron = h E = Ef – Ei = h Minus sign: free electron has zero energy Line spectrum Photoelectric effect:

Bohr Energy Levels

Electrons • All electrons have same charge and mass • Electrons have properties of waves and particles (De Broglie)

Heisenberg Uncertainty Principle Cannot simultaneously know the position and momentum of electron x = h Recognition that classical mechanics don’t work at atomic level.

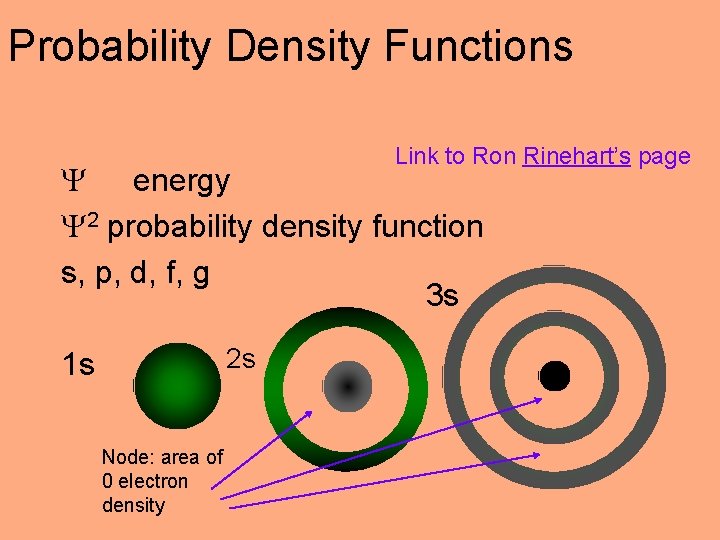
Schrödinger Equation Erwin Schrödinger 1926 Wave functions with discrete energies Less empirical, more theoretical n E n n wave functions or orbitals n 2 probability density functions

Quantum Numbers Each orbital defined by 3 quantum numbers Quantum number: number that labels state of electron and specifies the value of a property

Quantum Numbers Principal quantum number, n (shell) Specifies energy of electron (analogous to Bohr’s n) Average distance from nucleus n = 1, 2, 3, 4…. .

Quantum Numbers Azimuthal quantum number, (subshell) = 0, 1, 2… n– 1 n = 1, = 0 n = 2, = 0 or 1 n = 3, = 0, 1, or 2 Etc. 0 1 2 3 4 s p d f g

Quantum Numbers Magnetic quantum number, m Describes the orientation of orbital in space m = – …. + If = 2, m = – 2, – 1, 0, +1, +2

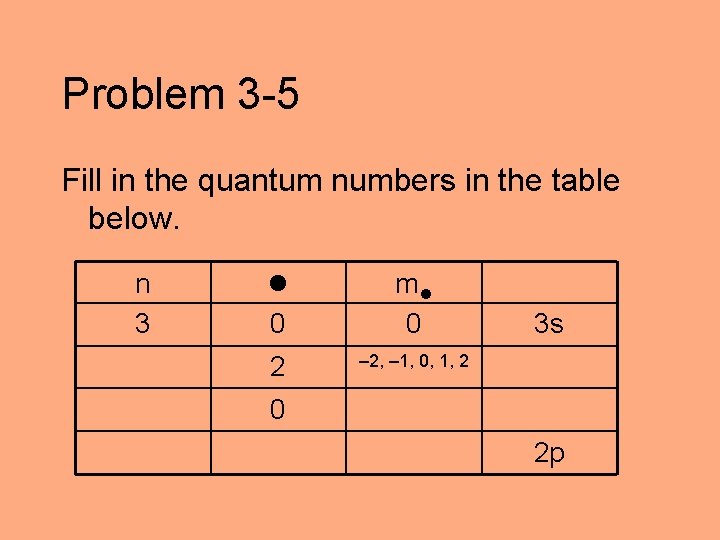
Problem 3 -5 Fill in the quantum numbers in the table below. n 3 0 m 0 2 – 2, – 1, 0, 1, 2 3 s 0 2 p

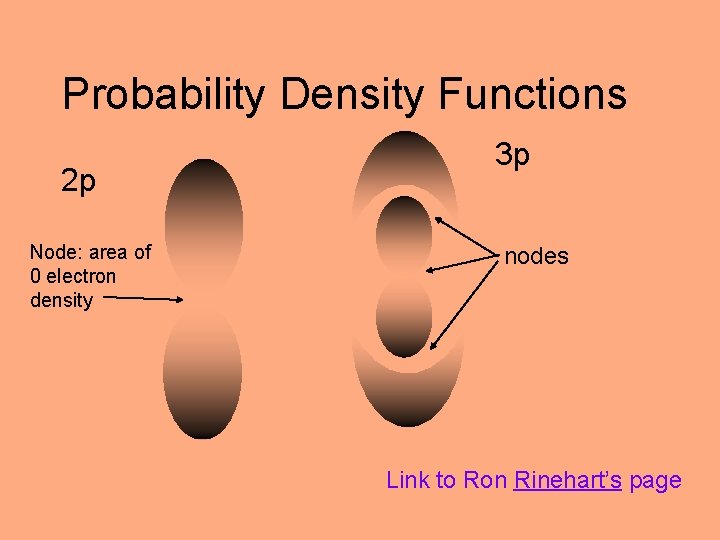
Schrödinger Equation Wave equations: Each electron has & E associated w/ it Probability Density Functions: 2 -graphical depiction of high probability of finding electron

Probability Density Functions Link to Ron Rinehart’s page energy 2 probability density function s, p, d, f, g 3 s 2 s 1 s Node: area of 0 electron density

Probability Density Functions 2 p Node: area of 0 electron density 3 p nodes Link to Ron Rinehart’s page

Electrons and Orbitals Pauli Exclusion Principle: no two electrons in the same atom may have the same quantum numbers Electron spin quantum number ms = ½ Electrons are spin paired within a given orbital

Electrons and Orbitals n=1 = 0, ms = ½ 2 electrons possible: 1, 0, 0, +½ and 1, 0, 0, –½ 2 electrons per orbital 1 s 1 H 1 s 2 He

Electrons and Orbitals n=2 = 0, ms = ½ 2, 0, 0, ½ 2 electrons possible n=2 = 1, m = – 1, 0, +1, ms = ½ 2, 1, – 1, ½ 2, 1, 0, ½ 2, 1, +1, ½ 6 electrons possible

Electron Configurations n=1 1 s 2 electrons possible H 1 e– 1 s 1 He 2 e– 1 s 2

Electron Configurations n=2 2 s 2 electrons possible Li Be 3 e– 1 s 2 4 e– 1 s 2 2 s 1 2 s 2 2 s 1 s

Electron Configurations n=2 2 p = 1, m = – 1, 0, +1 3 x 2 p orbitals (px, py, pz): 6 electrons possible 2 p – 2 2 1 B 5 e 1 s 2 s 2 p 2 s 1 s

Electron Configurations n=2 2 p = 1, m = – 1, 0, +1 3 x 2 p orbitals (px, py, pz): 6 electrons possible 2 p – 2 2 1 B 5 e 1 s 2 s 2 p 2 s 1 s

Electron Configurations n=2 2 p = 1, m = – 1, 0, +1 C 6 e– 1 s 2 2 p 2 2 p Hund’s Rule: for degenerate orbitals, the lowest energy is attained when electrons w/ same spin is maximized 2 s 1 s

Problem 3 -6 Write electron configurations and depict the electrons for N, O, F, and Ne.

Electron Configurations n=3 3 s, 3 p, 3 d Na 11 e– 3 p 3 s 1 s 2 2 p 63 s 1 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d Mg 12 e– 3 p 3 s 1 s 2 2 p 63 s 2 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d 3 p 3 s Al 13 e– 1 s 2 2 p 63 s 23 p 1 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d 3 p 3 s Si 14 e– 1 s 2 2 p 63 s 23 p 2 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d 3 p 3 s P 15 e– 1 s 2 2 p 63 s 23 p 3 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d 3 p 3 s S 16 e– 1 s 2 2 p 63 s 23 p 4 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d 3 p 3 s Cl 17 e– 1 s 2 2 p 63 s 23 p 5 2 p 2 s 1 s

Electron Configurations n=3 3 s, 3 p, 3 d 3 p 3 s Ar 18 e– 1 s 2 2 p 63 s 23 p 6 2 p 2 s 1 s

Electron Configurations 3 d vs. 4 s Filling order 1 s 2 s 3 s 4 s 5 s 6 s 7 s 2 p 3 p 4 p 5 p 6 p 7 p 3 d 4 d 5 d 6 d 4 f 5 f 5 g

Electron Configurations 4 p K 3 d 4 s 3 p 3 s 2 p 2 s 1 s

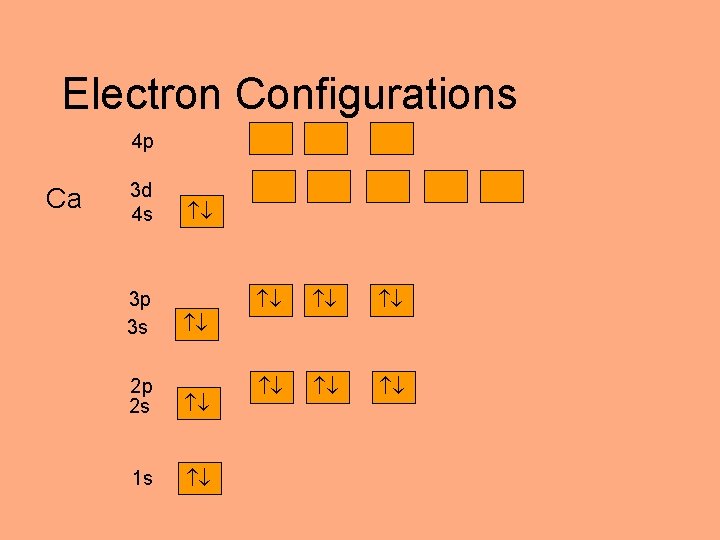
Electron Configurations 4 p Ca 3 d 4 s 3 p 3 s 2 p 2 s 1 s

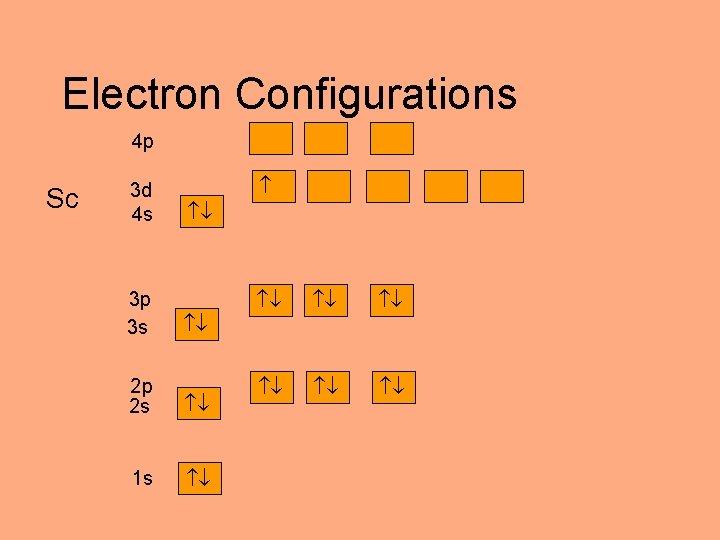
Electron Configurations 4 p Sc 3 d 4 s 3 p 3 s 2 p 2 s 1 s

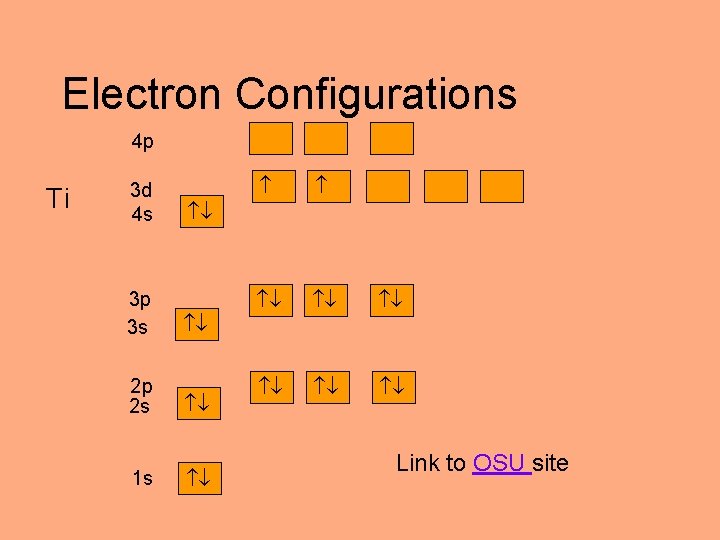
Electron Configurations 4 p Ti 3 d 4 s 3 p 3 s 2 p 2 s 1 s Link to OSU site

Problem 3 -7 Write the electron configurations for the transition metals V – Zn. Fill in the corresponding boxes to denote the electronic spin.