3 A Percentages Absolute and Relative Differences Percentage

§ 3. A – Percentages, Absolute and Relative Differences

Percentage

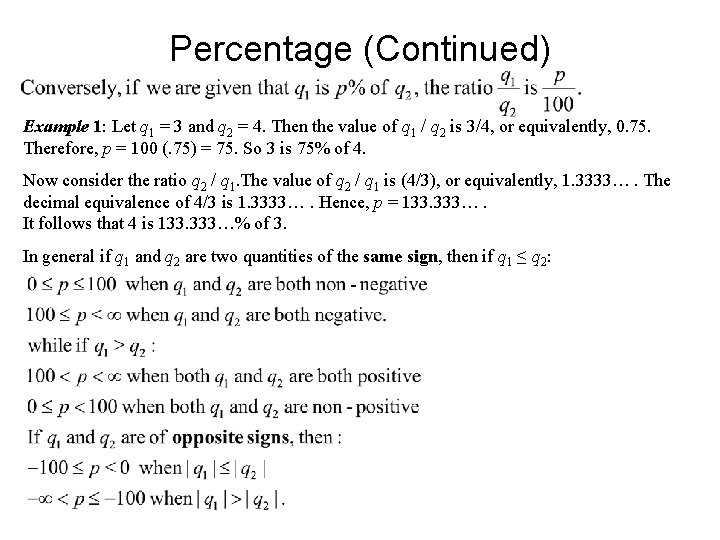
Percentage (Continued) Example 1: Let q 1 = 3 and q 2 = 4. Then the value of q 1 / q 2 is 3/4, or equivalently, 0. 75. Therefore, p = 100 (. 75) = 75. So 3 is 75% of 4. Now consider the ratio q 2 / q 1. The value of q 2 / q 1 is (4/3), or equivalently, 1. 3333…. The decimal equivalence of 4/3 is 1. 3333…. Hence, p = 133. 333…. It follows that 4 is 133. 333…% of 3. In general if q 1 and q 2 are two quantities of the same sign, then if q 1 ≤ q 2:

Percentage (Continued) Now, let us consider the special case of percent equivalence of q 1/q 2 when q 2 is 100. In this case, p = 100 (q 1/100) = q 1. We see that q 1 is q 1% of 100 (from the equivalent statement of percent). In this case, we interpret p = q 1 as the rate per 100. Example 2: A junk bond pays $1. 40 for each $35 dollar bond purchased. The ratio of $1. 40/$35 is 0. 04. So, p = 4. The bonds pay at a rate of $4. 00 per $100 invested in the bonds. In general, when q 2 is not equal to 100, then we scale the ratio q 1/q 2 to the equivalent ratio of p/100 where p is the percent equivalence. Example 3: A supermarket is selling sirloin steak at $21. 00 per 4 pounds. What is the rate per 100 pounds? Solution: The ratio of price/weight is $21. 00/4 pounds = $5. 25/pound. So, the rate is p = $525/100 pounds

Percentages Arising in Part-to-Part and Partto-Whole Examples Example 4: On a MTH 154 test, the following scores were obtained for the 10 people in the class: 5 15 18 30 35 37 69 83 90 95. What is the percentage of students with scores below class average compared to the students with scores above class average? What percentage of the class had scores above class average. Solution: The class average for all the 10 scores is 47. 7. There are six scores below that value and 4 scores above that value. So the percentage of students with scores below class average compared to student with scores above class average is p = 100 (6/4) = 150% This result says that the number of students with grades below class average was 1. 5 times the number of students with grades above class average. The is an example of part-to-part comparisons expressed as a percent. The total class has 10 students of which 4 had test scores above class average. The percentage of students with scores above class average is p = 100 (4/10) = 40%. This is an example of part-to-whole comparisons expressed as a percent.

Percentages Arising in Part-to-Part and Part-to. Whole Problems (Continued) Example 5: The Big Box Store is selling a 4 K HD television for a sale price of $950. When not on sale, the same television sells for $1362. What percent discount should the Big Box Store advertise in its sale literature? How much more in percent would a person have to pay if he/she does not take advantage of the sale? Solution: The normal selling price of the television is $1362. The sale price is $950. The markdown is $1362 – $950 = $412. The ratio of the markdown to the normal selling price is $412/$1362 = 0. 3025. Therefore p = 30. 25% the percentage markdown. (This is a part-to-whole comparison). The Big Box Store will probably say that the television is marked down greater than 30%. Suppose that a person misses the sale and buys the television at the non-sale price. Then compared to the sale price, the customer would be paying $1362 - $950 = $412 more than the customer that bought the television at the sale price. So the person would have to pay $412 more compared to the $950 sale price. The ratio of increased price to the sale price is $412/$950 = 0. 4337. So the customer would have to pay 43. 37% more than the customer who purchased the television on sale. (This is a part-to-part comparison). You will note that the markdown from the original price and the increase from the sale price are both $412. The reason that the markdown percent and the percent increase from the sale price are not the same is that the $412 is being compared to two different quantities (or bases), where the base is the denominator of the ratio.

Absolute and Relative Difference Let q 1 and q 2 be two numeric quantities. The absolute difference from q 1 to q 2 is q 2 – q 1. In Example 5, q 1 is the usual price of the television while q 2 is the sale price. Then the absolute difference from the usual price to the sale price for the television is –$412. The absolute difference is negative because it is a markdown to the sale price from the usual price. If we compare the absolute difference to one or the quantities q 1 or q 2 by taking the ratio of the (absolute difference)/q 1 or the (absolute difference)/q 2, we get the relative difference with respect to the bases q 1 or q 2 respectively. We usually express the relative difference as a percent. Again let us look at Example 5. Let q 2 be the sale price of the television and let q 1 be the usual selling price of the television. To see how much more a person would have to pay if he/she didn’t take advantage of the sale, we are going from the sale price to the usual price. The absolute difference is $412. So the relative difference with respect to q 2 is $412/$950 = 0. 4337 expressed as a percent, i. e. , 43. 37%. Another way of looking at this number is: sale price + (43. 37%)(sale price) = usual selling price. This makes complete sense since $950 + (0. 4337)($950) = $950(1+ 0. 4337) = $1362 (except for rounding error). The price grows 43. 37% from the sale price to get the usual selling price.

Absolute and Relative Difference (Continued) To find the relative difference with respect to the usual selling price, we are going from q 1 to q 2. So the absolute difference is – $412 and thus, the relative difference is – $412/$1362 = – 0. 3025 or – 30. 25%. What this is saying is that to go from the usual selling price to the sale price, there is a markdown of 30. 25% of the usual selling price. Again, this makes sense because $1362 – (0. 3025)($1362) = $1362(1 – 0. 3025) = $950 (except for rounding error. ) We saw two terms of the form (1 + x%) and (1 – y%) where x% and y% were expressed as decimals, (1 + 0. 4337) and (1 – 0. 3025) respectively. Quantities of the form (1 + x%) are called growth factors. Quantities of the form (1 – y%) are called decay factors. Sometimes we are given data in percents, where no value of a base is discernable. We can still talk about absolute and relative differences of percentages. Let p 1 and p 2 be two percentages. Then the absolute difference from p 1 to p 2 is p 2 – p 1, measured in percentage points (pp). Example 6: Suppose p 1 = 13. 5% and p 2 = 8. 7% then the absolute difference from p 1 to p 2 is 8. 7 – 13. 5 pp = – 4. 8 pp.

Absolute and Relative Difference (Continued) The relative difference with respect to either p 1 or p 2 is defined as (absolute difference)/p 1 or (absolute difference)/p 2 respectively, where the absolute difference is measured in pp. The relative difference is expressed as a percent. Example 7: The percent of cars painted white has gone from 33% in 2003 to 14. 5% in 2009. What is the relative difference in percentage from 2003 to 2009? Solution: The absolute difference is 14. 5% – 33% = – 18. 5 pp. The relative difference is – 18. 5 pp / 33% = – 56. 06%.