3 A HIDROGNATOM SZERKEZETE 1 3 1 A





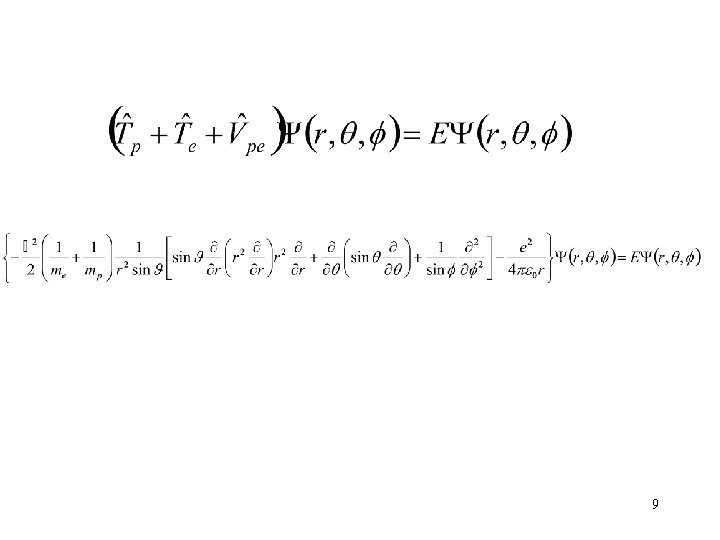










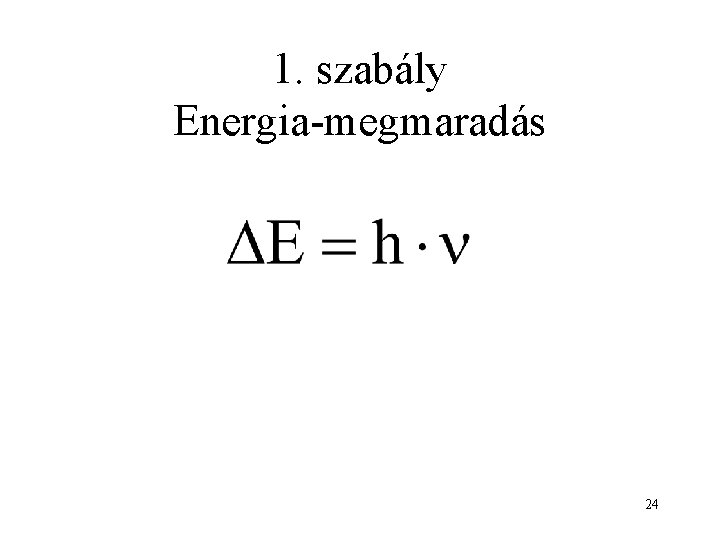





























- Slides: 65

3. A HIDROGÉNATOM SZERKEZETE 1

3. 1. A hidrogénatom Schrödinger -egyenlete 2

A hidrogénatom klasszikus mechanikai modellje + Pozitív töltésű részecske, amely körül egy negatív töltésű részecske mozog („kering”). 3

A kvantummechanika Schrödinger-egyenlete általános formában 4

A hidrogénatom Schrödinger-egyenlete Megj. : alsó indexben e és p elektronra, ill. protonra utal, e elemi töltés (1, 602 x 10 -19 C), elektron töltése -e r az elektron protontól való távolsága, vákuum permittivitás (8, 854 10 -12 Fm-1). 5

A hidrogénatom Schrödingeregyenlete megoldható! A megoldás trükkje: polár-koordináta rendszert alkalmazunk. 6

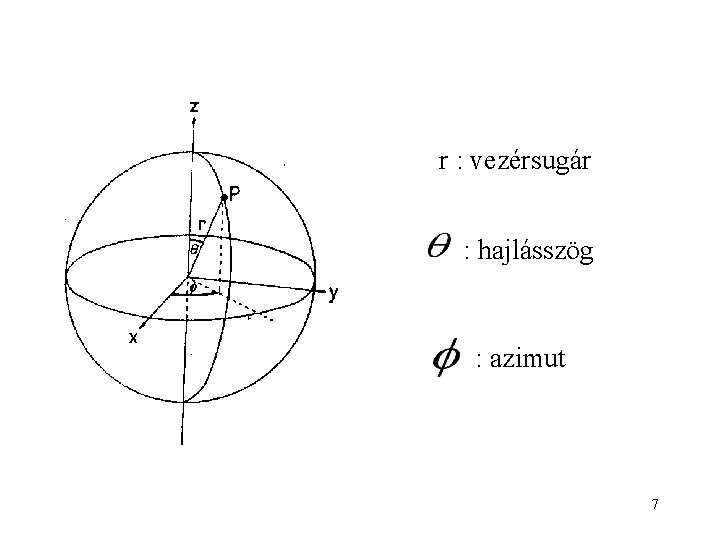
r : vezérsugár : hajlásszög : azimut 7

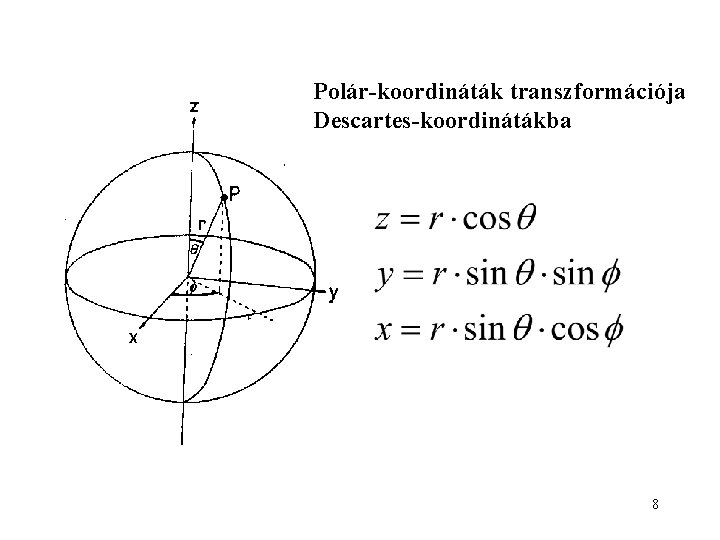
Polár-koordináták transzformációja Descartes-koordinátákba 8
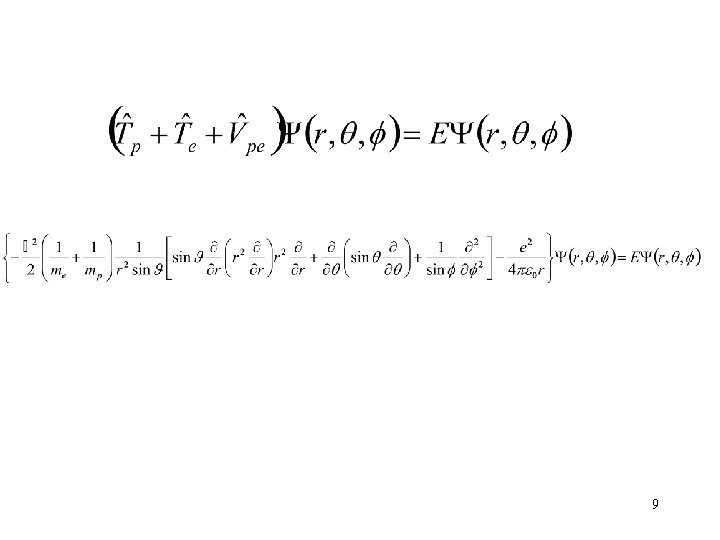
9

A Schrödinger-egyenlet megoldása Sajátérték n: főkvantumszám 1, 2, 3. . . 10

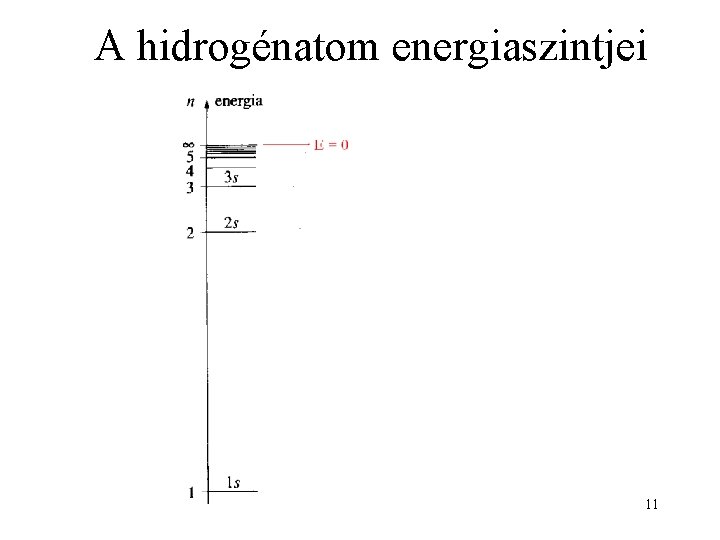
A hidrogénatom energiaszintjei 11

A Schrödinger-egyenlet megoldása Sajátfüggvények („atompályák”) Három egész számot tartalmaznak 12

A Schrödinger-egyenlet megoldása Degenerált állapotok Azonos az energia (sajátérték), de különféle sajátfüggvények tartoznak hozzá. Ha n megegyezik, de és/vagy m nem, azok a H-atom degenerált állapotai 13

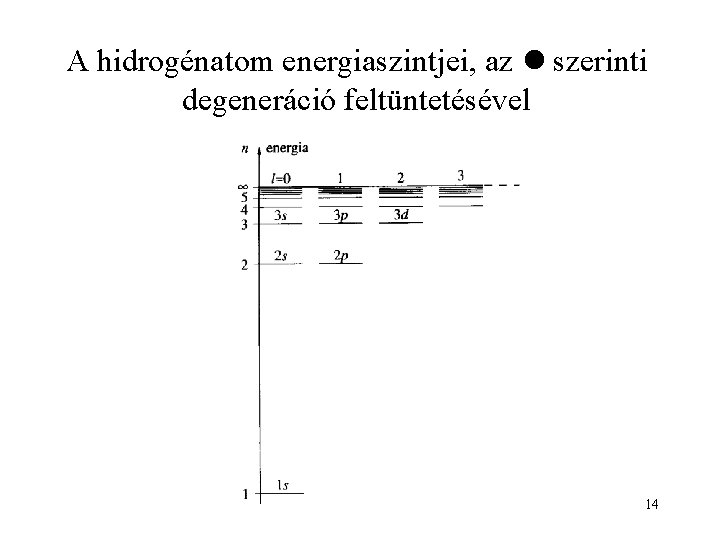
A hidrogénatom energiaszintjei, az szerinti degeneráció feltüntetésével 14

A sajátfüggvények alakja radiális rész anguláris (szögtől függő) rész 15

A hidrogénatom hullámfüggvényei 16

A hidrogénatom komplex hullámfüggvényei 17

Lineár-kombinációk (ábrázolhatóság miatt) 18

A hidrogénatom valós hullámfüggvényei 19

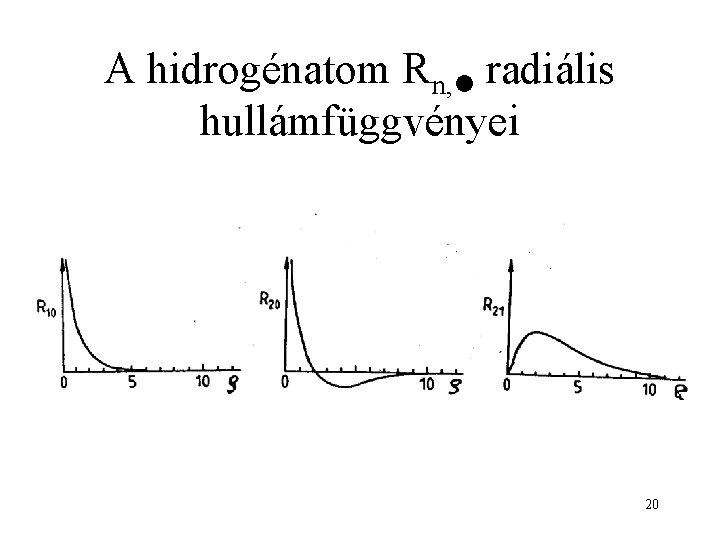
A hidrogénatom Rn, radiális hullámfüggvényei 20

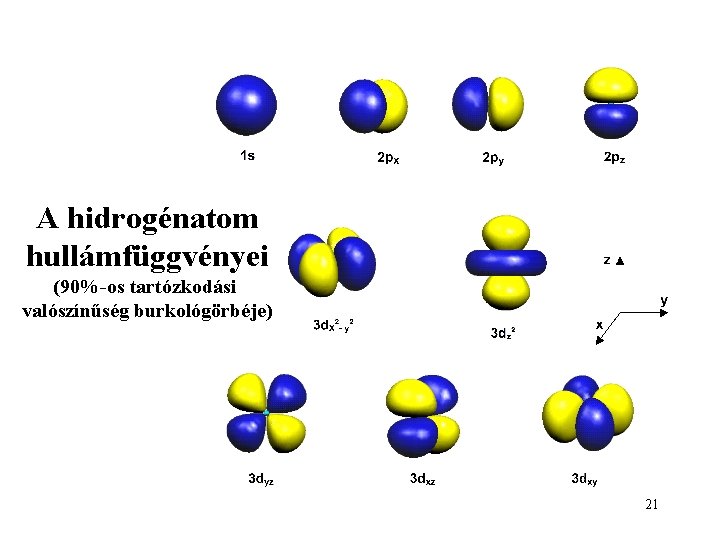
A hidrogénatom hullámfüggvényei (90%-os tartózkodási valószínűség burkológörbéje) 21

3. 2 A hidrogénatom színképe 22

Kiválasztási szabályok: az elektromágneses sugárzás elnyelésének/kibocsátásának feltételei (Levezethető kvantummechanika axiómából) 23
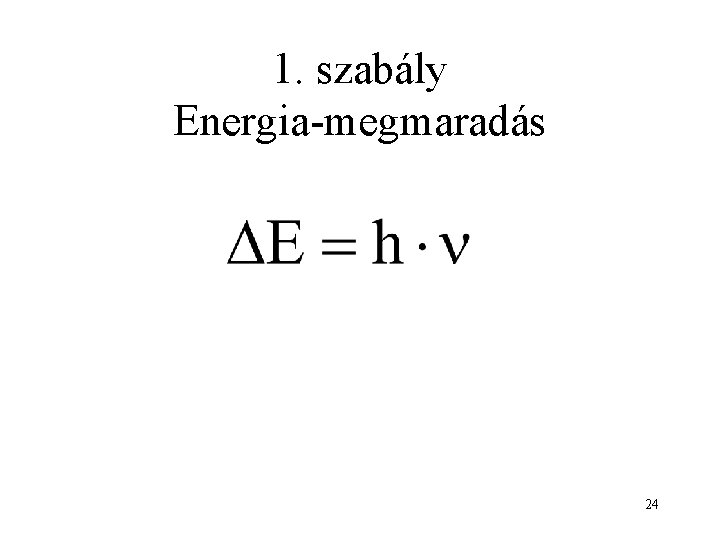
1. szabály Energia-megmaradás 24

Átmeneti momentum és állapotfüggvény 1 -es index: kiindulási állapotban dipólus-momentum operátor 2 -es index: végállapotban P 2 , az átmeneti momentum négyzete arányos az átmenet valószínűségével – azaz a spektrumvonal intenzitásával 25

Dipólus momentum d - + egy pozitív és egy negatív töltés q : a töltés d: a távolság; a negatív töltéstől a pozitív töltés irányába mutat 26

Több töltés esetén q : a töltés 27

Hidrogénatomra vonatkozó kiválasztási szabályok bármennyi 29

A hidrogénatom színképe diszkrét vonalak! 30

Az atomos hidrogén spektruma 31

Az atomos hidrogén spektruma látható tartomány: Balmer-széria 32

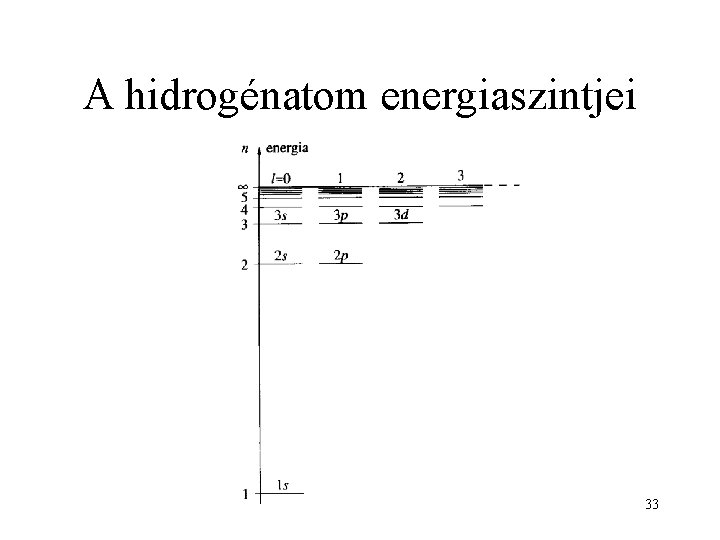
A hidrogénatom energiaszintjei 33

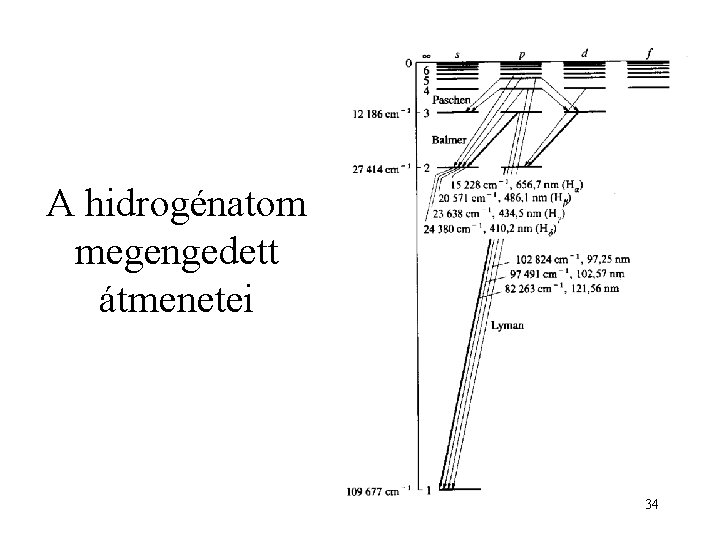
A hidrogénatom megengedett átmenetei 34

A hidrogénatom vonalszériái 35

3. 3 -3. 4 A hidrogénatom elektronjának impulzusmomentuma és mágneses momentuma (Előadás alapján) 36

Mikrorendszerek kvantált fizikai mennyiségei • • • E energia L impulzusmomentum absz. értéke (vektorhossz) Lz impulzus-momentum z-irányú vetülete M mágneses momentum abszolút értéke Mz mágneses momentum z-irányú vetülete 37

A klasszikus mechanikában körmozgást végző testre m: tömeg 38

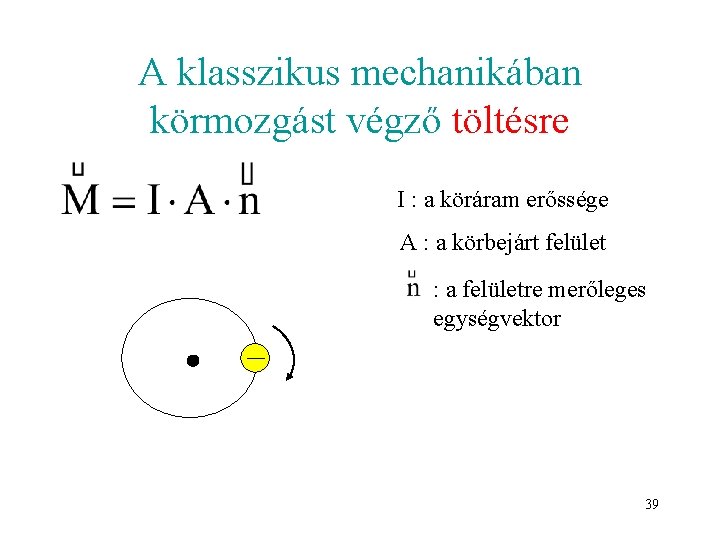
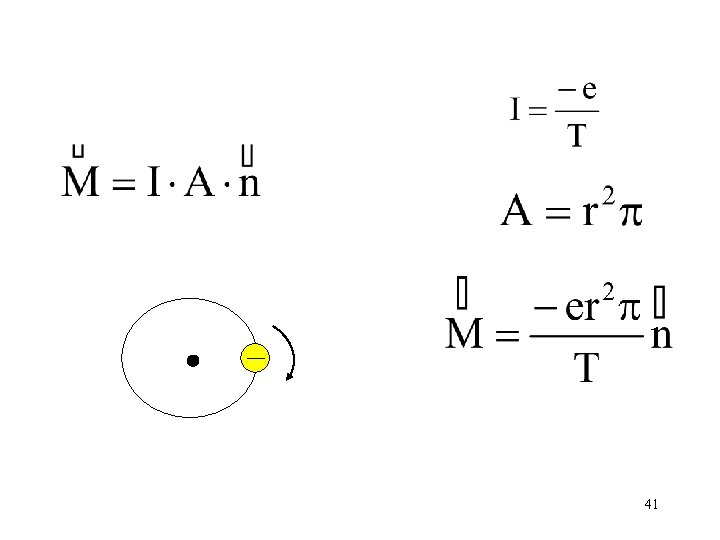
A klasszikus mechanikában körmozgást végző töltésre I : a köráram erőssége A : a körbejárt felület : a felületre merőleges egységvektor 39

Próbáljuk meg összefüggésbe hozni az impulzus-momentummal! 40

41

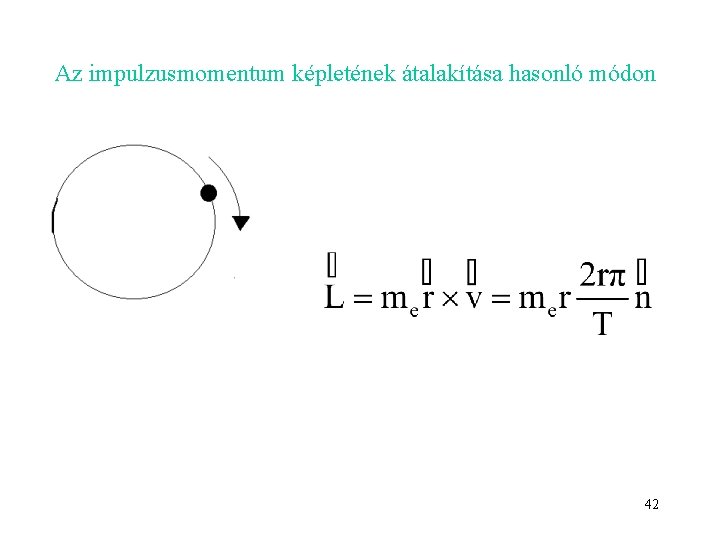
Az impulzusmomentum képletének átalakítása hasonló módon 42

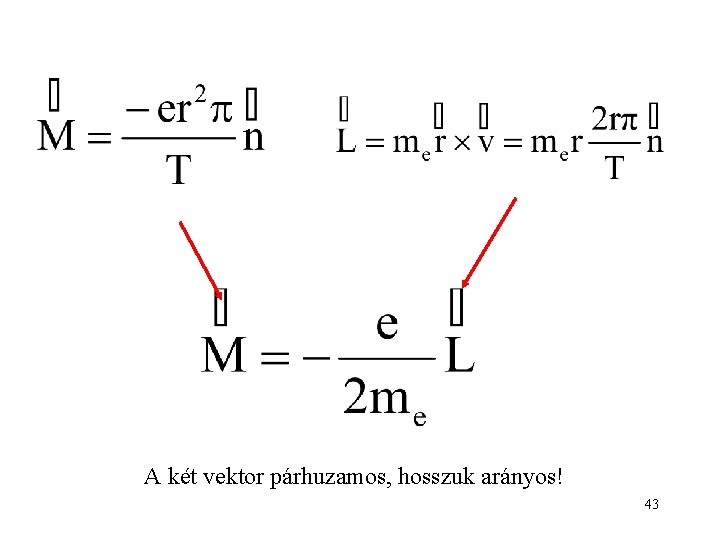
A két vektor párhuzamos, hosszuk arányos! 43

H-atomra kvantum-mechanikai levezetéssel az operátor sajátérték-egyenletét megoldva , azaz mellék-kvantumszám az operátor sajátérték-egyenletét megoldva m: mágneses kvantumszám 44

H-atomra és összefüggése alapján Bohr-magneton 45

H-atomra és összefüggése alapján m : mágneses kvantumszám 46

Mágneses térben levő részecske potenciális energiája Klasszikus fizika: Kvantummechanika : mágneses indukció 47

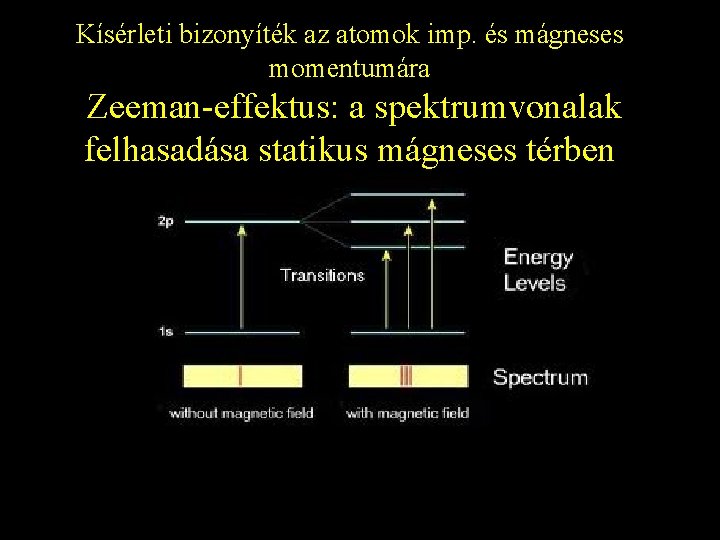
Kísérleti bizonyíték az atomok imp. és mágneses momentumára Zeeman-effektus: a spektrumvonalak felhasadása statikus mágneses térben 48

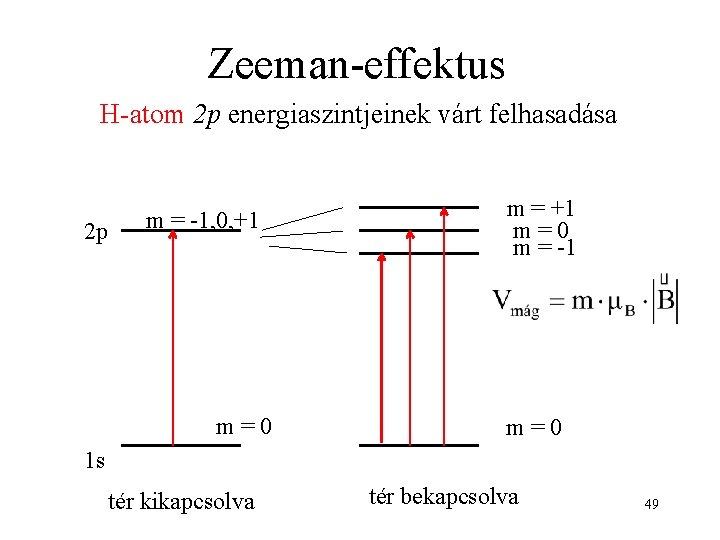
Zeeman-effektus H-atom 2 p energiaszintjeinek várt felhasadása 2 p m = -1, 0, +1 m=0 m = -1 m=0 1 s tér kikapcsolva tér bekapcsolva 49

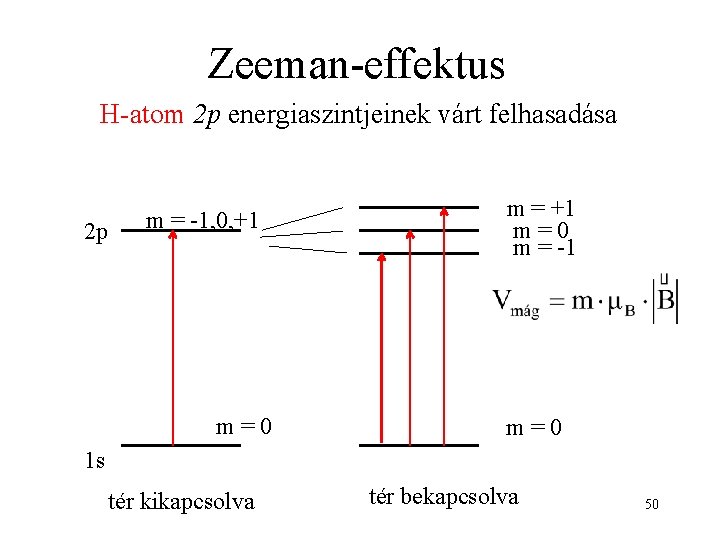
Zeeman-effektus H-atom 2 p energiaszintjeinek várt felhasadása 2 p m = -1, 0, +1 m=0 m = -1 m=0 1 s tér kikapcsolva tér bekapcsolva 50

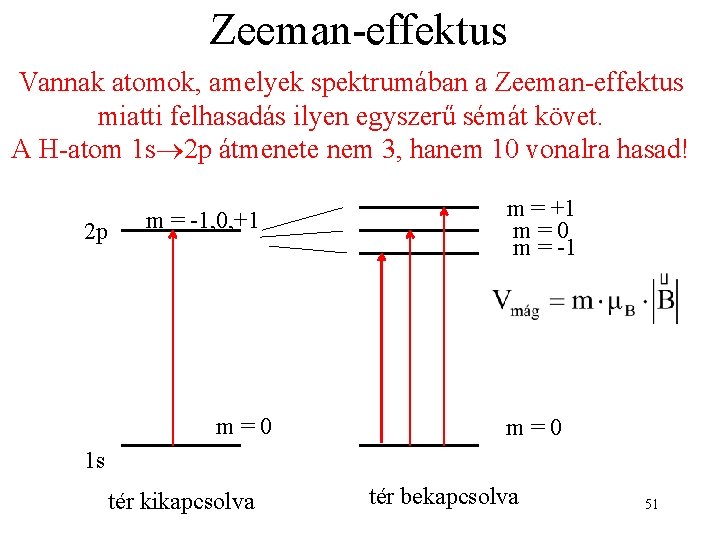
Zeeman-effektus Vannak atomok, amelyek spektrumában a Zeeman-effektus miatti felhasadás ilyen egyszerű sémát követ. A H-atom 1 s 2 p átmenete nem 3, hanem 10 vonalra hasad! 2 p m = -1, 0, +1 m=0 m = -1 m=0 1 s tér kikapcsolva tér bekapcsolva 51

3. 5 Az elektronspin 52

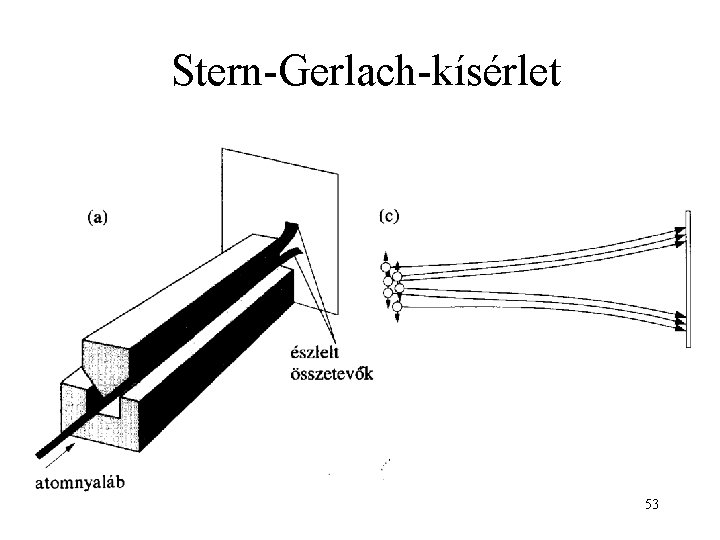
Stern-Gerlach-kísérlet 53

Kísérlet ezüst-atom sugárral (hidrogénatommal a kísérlet nehezebb, de az eredmény hasonló. ) Alapáll. : n =1; és m csak 0 lehet! nem térül el Eredmény: két irányba eltérül!! 54

Értelmezés Alapállapotban is van impulzusmomentum, amelyből mágneses momentum adódik. Ez az impulzusmomentum a spin. Jele: abszolút értéke: S z-irányú vetülete: Sz 55

Az elektron spinje : spinre utaló mellék-kvantumszám s spin-kvantumszám (spinre utaló mágneses kvantumszám) 56

Spinből származó mágneses momentum abszolút érték z irányú komponens ge : Lande-faktor hidrogénatomban ge=2, 0023 57

A spinból származó mágneses momentum magyarázza a Stern-Gerlach kísérletet! 58

Spin értelmezése: Paul Dirac (1902 -1984) Relativisztikus kvantummechanika 59

Relativitáselmélet • Olyan mozgások leírása, ahol a sebesség összemérhető a fénysebességgel. • Az elektron sebessége is összemérhető a fénysebességgel. • Dirac-egyenlet: Schrödinger egyenlet módosítva a relativitáselmélettel. 60

A hidrogénatom Diracegyenletének megoldása Újabb kvantumszám: belső kvantumszám : az elektronpálya impulzusmomentumát jell. kvantumszám : a spin impulzusmomentumát jell. kvantumszám ha s pálya p pálya d pálya E függ n-től nagyon és j-től picit 61

Spin-pálya felhasadás p pálya d pálya Ha 0 -től eltér a mellék-kvantumszám, a belső kvantumszám szerint az energiaszintek kétfelé hasadnak. 62

A Dirac-egyenlet sajátfüggvényei „spin-koordináta” 63

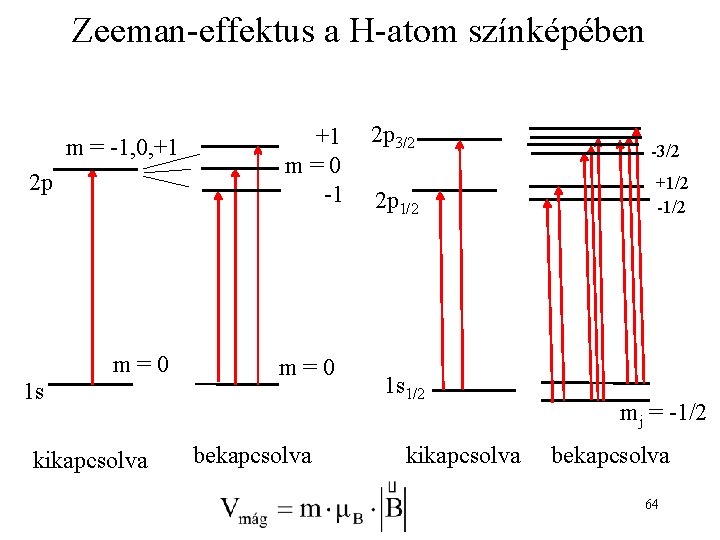
Zeeman-effektus a H-atom színképében m = -1, 0, +1 2 p 1 s m=0 kikapcsolva +1 m=0 -1 m=0 bekapcsolva 2 p 3/2 2 p 1/2 1 s 1/2 kikapcsolva -3/2 +1/2 -1/2 mj = -1/2 bekapcsolva 64

Alapkérdések 15. Miből származik a H-atom potenciális energiája? Írja fel a képletét! 16. Rajzolja fel a H-atom energiaszintjeinek sémáját! 17. Mit nevezünk a kvantummechanikában degenerált állapotoknak? 18. Milyen kvantumszámokkal jellemezhető a H-atom állapota? Milyen értékeket vehetnek fel ezek a kvantumszámok? 19. Mit nevezünk a spektroszkópiában kiválasztási szabályoknak? ˙/ . 65

Alapkérdések 20. Írja fel az átmeneti momentum képletét! 21. Írja fel a hidrogénatom pályaimpulzusmomentumvektorának hosszára és z-irányú vetületére vonatkozó sajátértékeket! 22. Írja fel a mágneses momentum képletét! 23. Mit nevezünk Zeeman-effektusnak? 24. Írja fel az elektron spin-impulzusmomentumának hosszára és z-irányú vetületére vonatkozó sajátértékeket! 66