3 9 Determinants Given a square matrix A























- Slides: 24

3. 9 Determinants • Given a square matrix A its determinant is a real number associated with the matrix. • The determinant of A is written: det(A) or |A| • For a 2 x 2 matrix, the definition is a b det = = ad - bc c d • For larger matrices the definition is more complicated

Determinants 2 x 2 examples 1 2 det 3 4 1 2 = 3 4 = (1)(4) – (2)(3) = -2 -5 2 det -2 0 -5 2 = -2 0 = (-5)(0) – (2)(-2) = 4 1 2 det 2 4 1 2 = 2 4 = (1)(4) – (2)(2) = 0

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 11 : remove row 1, col 1 2 3 M 11 = 7 0

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 12 : remove row 1, col 2 -1 3 M 12 = 2 0

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 13 : remove row 1, col 3 -1 2 M 13 = 2 7

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 21 : remove row 2, col 1 1 -2 M 21 = 7 0

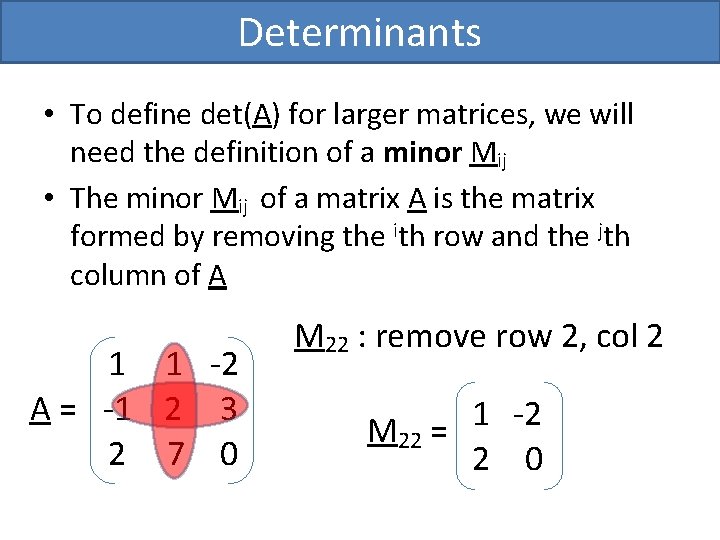
Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 22 : remove row 2, col 2 1 -2 M 22 = 2 0

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 23 : remove row 2, col 3 1 1 M 23 = 2 7

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 31 : remove row 3, col 1 1 -2 M 31 = 2 3

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 32 : remove row 3, col 2 1 -2 M 32 = -1 3

Determinants • To define det(A) for larger matrices, we will need the definition of a minor Mij • The minor Mij of a matrix A is the matrix formed by removing the ith row and the jth column of A 1 1 -2 A = -1 2 3 2 7 0 M 33 : remove row 3, col 3 1 1 M 33 = -1 2

3. 9. 1 The formula for a 3 x 3 matrix • For a matrix a 11 a 12 a 13 A = a 21 a 22 a 23 a 31 a 32 a 33 • Its determinant is given by |A| = a 11|M 11| - a 12|M 12| + a 13|M 13| • From the formula for a 2 x 2 matrix: a 22 a 23 |M 11|= = a 22 a 33 - a 23 a 32 a 33

3. 9. 1 The formula for a 3 x 3 matrix • For a matrix a 11 a 12 a 13 A = a 21 a 22 a 23 a 31 a 32 a 33 • Its determinant is given by |A| = a 11|M 11| - a 12|M 12| + a 13|M 13| • From the formula for a 2 x 2 matrix: a 21 a 23 |M 12|= = a 21 a 33 - a 23 a 31 a 33

3. 9. 1 The formula for a 3 x 3 matrix • For a matrix a 11 a 12 a 13 A = a 21 a 22 a 23 a 31 a 32 a 33 • Its determinant is given by |A| = a 11|M 11| - a 12|M 12| + a 13|M 13| • From the formula for a 2 x 2 matrix: a 21 a 22 |M 13|= = a 21 a 32 - a 31 a 22 a 31 a 32

3 x 3 Example 1 1 -2 A = -1 2 3 2 7 0 |A| = 1 x|M 11| - 1 x|M 12| + (-2)x|M 13| 2 3 |A|= 1 x 7 0 -1 3 - 1 x 2 0 -1 2 + (-2) 2 7 = 1 x(-21) -1 x(-6) +(-2)x(-11) = 7

3 x 3 Example 0 1 3 B= 5 3 1 -1 2 0 |B| = 0 x|M 11| - 1 x|M 12| + 3 x|M 13| 3 1 |B|= 0 x 2 0 5 1 5 3 - 1 x + 3 x -1 0 -1 2 = 0 x(-2) -1 x(1) +(3)x(13) = 38

3. 9. 1 The formula for a 3 x 3 matrix • For the matrix a 11 a 12 a 13 A = a 21 a 22 a 23 a 31 a 32 a 33 • We used the top row to calculate the determinant: |A| = a 11|M 11| - a 12|M 12| + a 13|M 13| • However, we could equally have used any row of the matrix and performed a similar calculation

3. 9. 1 The formula for a 3 x 3 matrix • For the matrix a 11 a 12 a 13 A = a 21 a 22 a 23 a 31 a 32 a 33 • Using the top row: |A| = a 11|M 11| - a 12|M 12| + a 13|M 13| • Using the second row |A| = -a 21|M 21| + a 22|M 22| - a 23|M 23| • Using the third row |A| = a 31|M 31| - a 32|M 32| + a 33|M 33|

3. 9. 1 The formula for a 3 x 3 matrix |A| = a 11|M 11| - a 12|M 12| + a 13|M 13| = -a 21|M 21| + a 22|M 22| - a 23|M 23| = a 31|M 31| - a 32|M 32| + a 33|M 33| • Notice the changing signs depending on what row we use: + - +

3. 9. 1 The formula for a 3 x 3 matrix • Equally, we could have used any column as long as we follow the signs pattern a 11 a 12 a 13 A = a 21 a 22 a 23 a 31 a 32 a 33 + - + • E. g. using the first column: |A| = a 11|M 11| - a 21|M 21| + a 31|M 31|

• This choice sometimes makes it a bit easier to calculate determinants. e. g. 1 1 -2 A= 0 2 3 0 1 1 • Using the first row: 2 3 |A|= 1 x 1 1 0 3 0 2 - 1 x + (-2) x 0 1 = 1 x(-1) -1 x(0) + (-2)x(0) = -1

• This choice sometimes makes it a bit easier to calculate determinants. e. g. 1 1 -2 A= 0 2 3 0 1 1 • However, using the first column: 2 3 |A|= 1 x 1 1 - 0 + 0 = 1 x(-1) = -1

3. 9. 2 A general formula for determinants • For a 4 x 4 matrix we add up minors like the 3 x 3 case, and again use the same signs pattern + + - + + • Notice that if we think of the signs pattern as a matrix, then it can be written as (-1)i+j

3. 9. 2 A general formula for determinants • For a nxn matrix A=(aij) the co-factors of A are defined by Cij: = (-1)i+j|Mij| • The determinant of A is given by the formula • Or, |A|= aij Cij for any j=1, 2, . . . , n |A|= aij Cij for any i=1, 2, . . . , n