3 8 Transforming Polynomial Functions Objective Transform polynomial

3 -8 Transforming Polynomial Functions Objective Transform polynomial functions. Holt Mc. Dougal Algebra 2

3 -8 Transforming Polynomial Functions You can perform the same transformations on polynomial functions that you performed on quadratic and linear functions. Holt Mc. Dougal Algebra 2

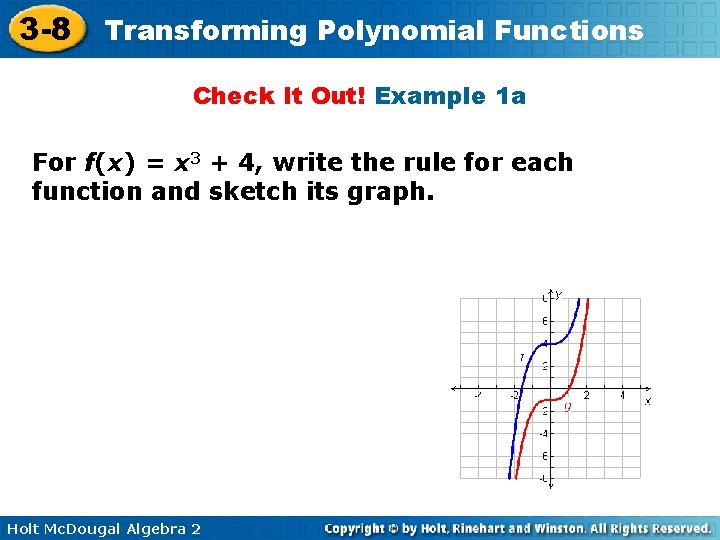
3 -8 Transforming Polynomial Functions Check It Out! Example 1 a For f(x) = x 3 + 4, write the rule for each function and sketch its graph. Holt Mc. Dougal Algebra 2

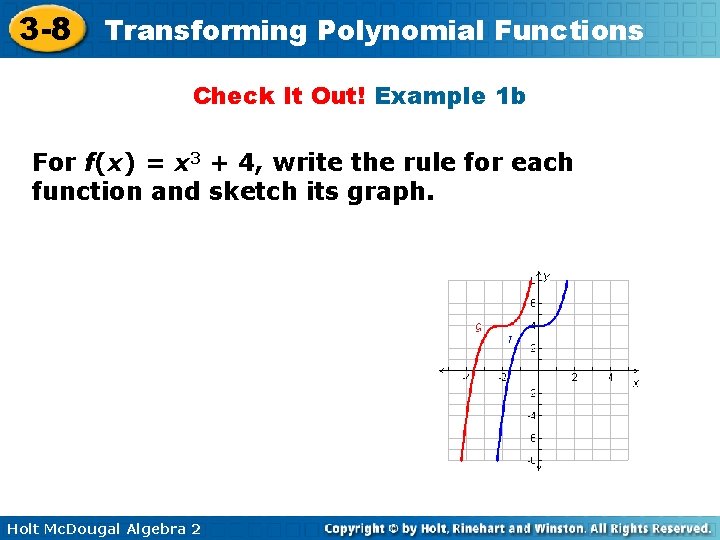
3 -8 Transforming Polynomial Functions Check It Out! Example 1 b For f(x) = x 3 + 4, write the rule for each function and sketch its graph. Holt Mc. Dougal Algebra 2

3 -8 Transforming Polynomial Functions Check It Out! Example 2 a Let f(x) = x 3 – 2 x 2 – x + 2. Write a function g that performs each transformation. Reflect f(x) across the x-axis. Holt Mc. Dougal Algebra 2

3 -8 Transforming Polynomial Functions Check It Out! Example 2 b Let f(x) = x 3 – 2 x 2 – x + 2. Write a function g that performs each transformation. Reflect f(x) across the y-axis. Holt Mc. Dougal Algebra 2

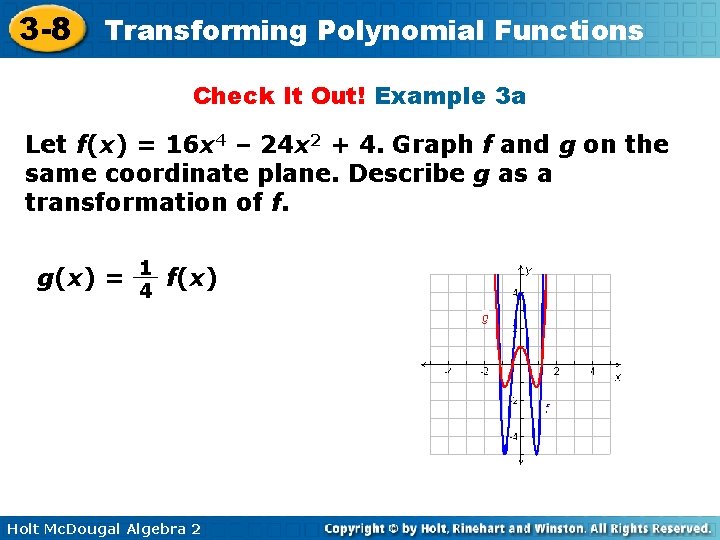
3 -8 Transforming Polynomial Functions Check It Out! Example 3 a Let f(x) = 16 x 4 – 24 x 2 + 4. Graph f and g on the same coordinate plane. Describe g as a transformation of f. g(x) = 1 f(x) 4 Holt Mc. Dougal Algebra 2

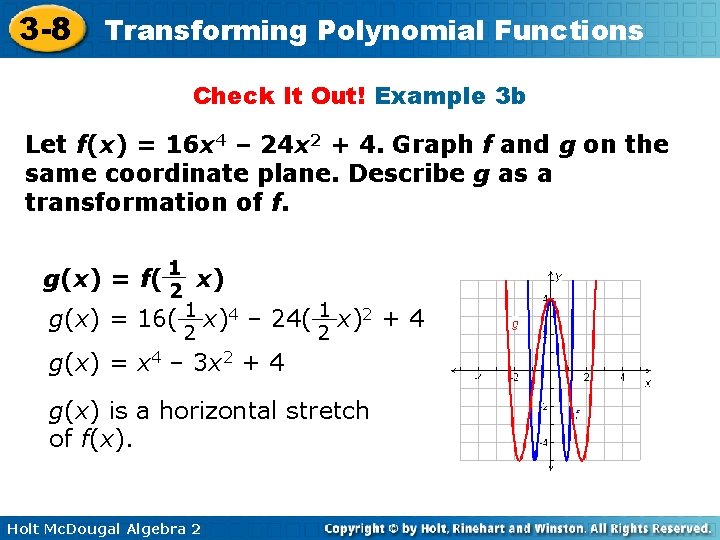
3 -8 Transforming Polynomial Functions Check It Out! Example 3 b Let f(x) = 16 x 4 – 24 x 2 + 4. Graph f and g on the same coordinate plane. Describe g as a transformation of f. g(x) = f( 1 x) 2 g(x) = 16( 1 x)4 – 24( 1 x)2 + 4 2 2 g(x) = x 4 – 3 x 2 + 4 g(x) is a horizontal stretch of f(x). Holt Mc. Dougal Algebra 2

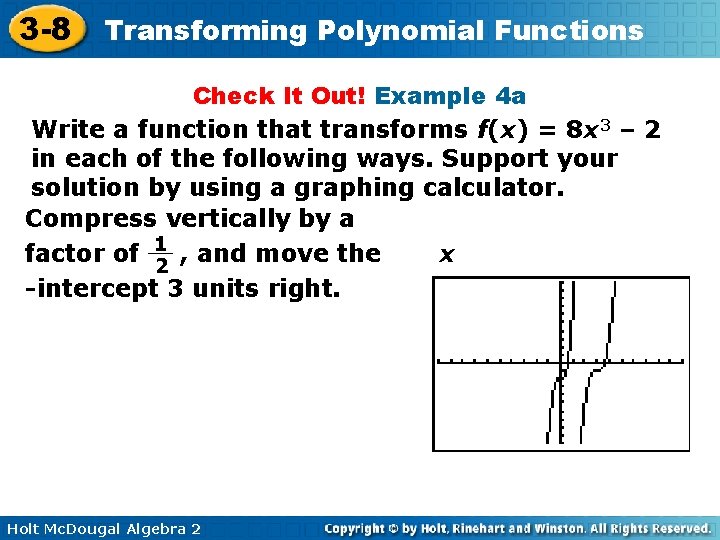
3 -8 Transforming Polynomial Functions Check It Out! Example 4 a Write a function that transforms f(x) = 8 x 3 – 2 in each of the following ways. Support your solution by using a graphing calculator. Compress vertically by a factor of 1 , and move the x 2 -intercept 3 units right. Holt Mc. Dougal Algebra 2

3 -8 Transforming Polynomial Functions Check It Out! Example 4 b Write a function that transforms f(x) = 6 x 3 – 3 in each of the following ways. Support your solution by using a graphing calculator. Reflect across the x-axis and move the x-intercept 4 units left. Holt Mc. Dougal Algebra 2