3 6 Parallel Lines in a Coordinate Plane

Goal 1: Slope of Parallel Lines o o In Algebra, you learned that the

Example 1: Finding the slope of train tracks o COG RAILWAY. A cog railway

Example 2: Finding Slope of a Line o o Find the slope of the

Postulate 17 Slopes of Parallel Lines o In a coordinate plane, two non-vertical lines

Example 3: Deciding Whether Lines are Parallel o Find the slope of each line.

Example 4 Identifying Parallel Lines M 1= 0 -6 = -3 2 -0 2

Solution Compare the slopes. Because k 2 and k 3 have the same slope,

Goal 2: Writing Equations of Parallel Lines o In Algebra, you learned that you

Example 5: Writing an Equation of a Line o Write an equation of the

Slides: 10

Download presentation

3. 6 Parallel Lines in a Coordinate Plane

Goal 1: Slope of Parallel Lines o o In Algebra, you learned that the slope of a nonvertical line is the ratio of the vertical change (rise) to the horizontal change (run). If the line passes through the points (x 1, y 1) and (x 2, y 2), then the slope is given by slope = rise run m = y 2 – y 1 x 2 – x 1 Slope is usually represented by the variable m.

Example 1: Finding the slope of train tracks o COG RAILWAY. A cog railway goes up the side of Mount Washington, the tallest mountain in New England. At the steepest section, the train goes up about 4 feet for each 10 feet it goes forward. What is the slope of this section? slope = rise = 4 feet =. 4 run 10 feet

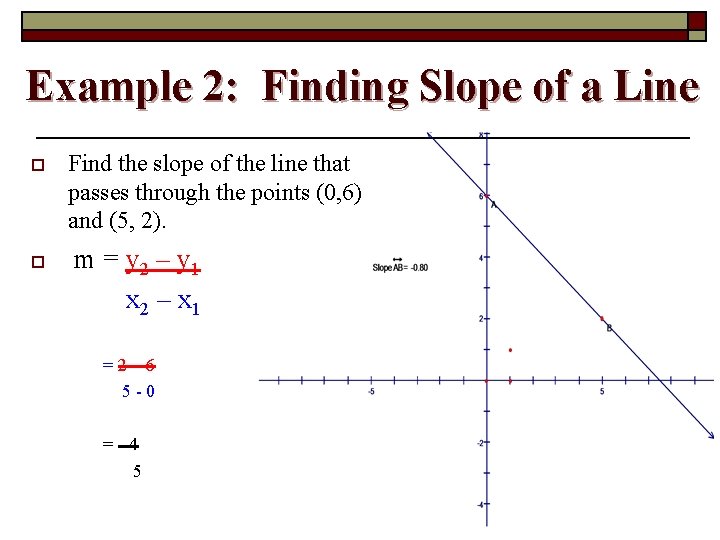
Example 2: Finding Slope of a Line o o Find the slope of the line that passes through the points (0, 6) and (5, 2). m = y 2 – y 1 x 2 – x 1 =2– 6 5 -0 =-4 5

Postulate 17 Slopes of Parallel Lines o In a coordinate plane, two non-vertical lines are parallel if and only if they have the same slope. Any two vertical lines are parallel. Lines k 1 and k 2 have the same slope. k 1 k 2

Example 3: Deciding Whether Lines are Parallel o Find the slope of each line. Is j 1║j 2? M 1 = M 2 = Because the lines have the same slope, j 1║j 2.

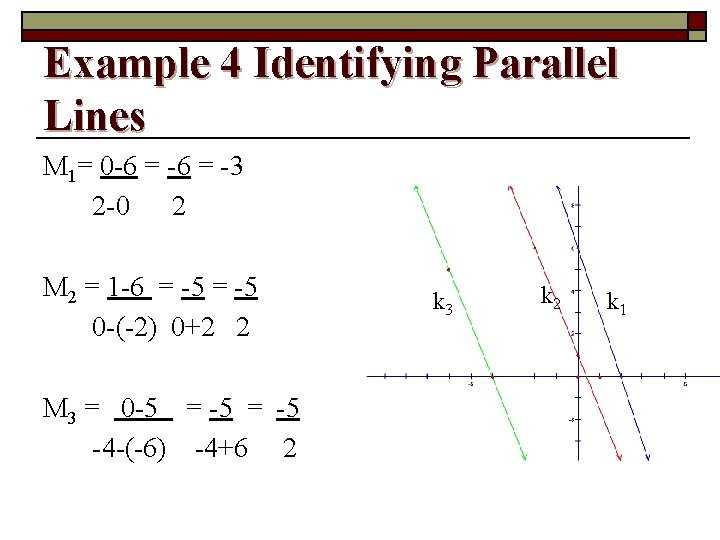
Example 4 Identifying Parallel Lines M 1= 0 -6 = -3 2 -0 2 M 2 = 1 -6 = -5 0 -(-2) 0+2 2 M 3 = 0 -5 = -5 -4 -(-6) -4+6 2 k 3 k 2 k 1

Solution Compare the slopes. Because k 2 and k 3 have the same slope, they are parallel. Line k 1 has a different slope, so it is not parallel to either of the other lines.

Goal 2: Writing Equations of Parallel Lines o In Algebra, you learned that you can use the slope m of a non-vertical line to write an equation of the line in slope-intercept form. slope y-intercept y = mx + b q The y-intercept is the y-coordinate of the point where the line crosses the y-axis.

Example 5: Writing an Equation of a Line o Write an equation of the line through the point (2, 3) that has a slope of 5. y = mx + b 3 = 5(2) + b 3 = 10 + b -7= b o Steps/Reasons why Given Slope-Intercept form Substitute 2 for x, 3 for y and 5 for m Multiply Subtract