3 5 Truth Trees Gregory Chapter 3 pp


















![The Tautology Test ¬ [(A → B) ∧ ¬ (¬ A ∨ B)] √ The Tautology Test ¬ [(A → B) ∧ ¬ (¬ A ∨ B)] √](https://slidetodoc.com/presentation_image_h2/b0816fceddf95d927b062c0842b1fd01/image-32.jpg)







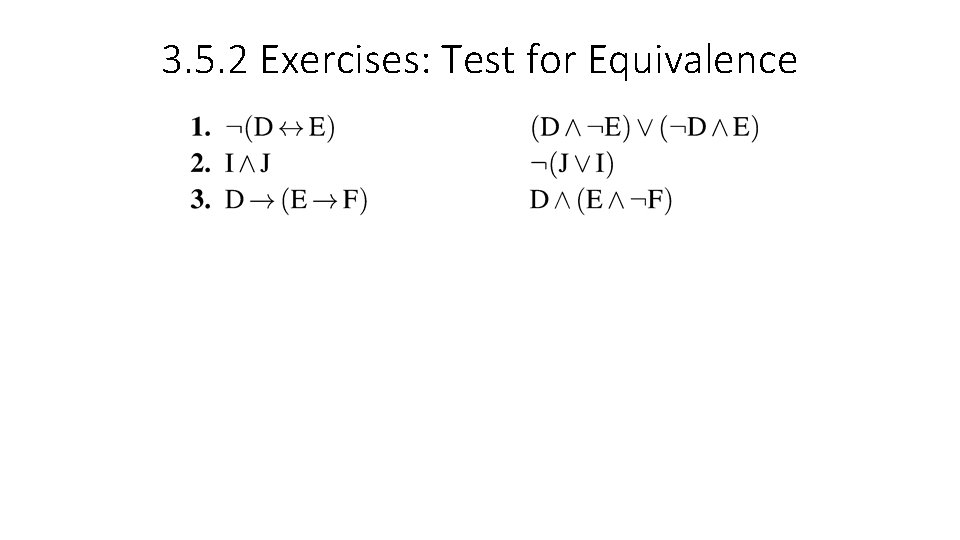


- Slides: 46

3. 5 Truth Trees Gregory Chapter 3 pp 87 - 104

Contents • Indirect Truth Tables • Truth Trees: Theory and Practice • Truth Tests for: - Consistency - Tautologousness - Equivalence - Validity

Truth Trees and Truth Tables • When we do a truth table to test for consistency, most of the work is wasted. • We just need know whethere’s a TVA that makes all sentence true or no TVA that makes all sentences true. • We can try to construct a TVA that assigns all sentences TRUE…working backward from the assignment of truth values to sentences to truth values of their parts. . .

Indirect Truth Table: Testing for Consistency ¬A ∨ B / ¬ A → B / ¬ A ∧ B

Indirect Truth Table: Testing for Consistency ¬ A ∨ B / A ∨ ¬ B / A → B

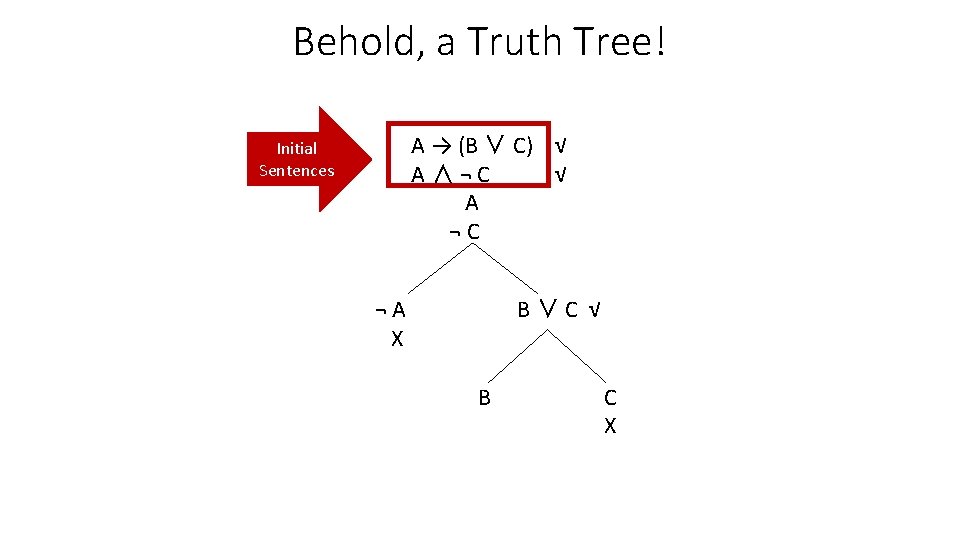
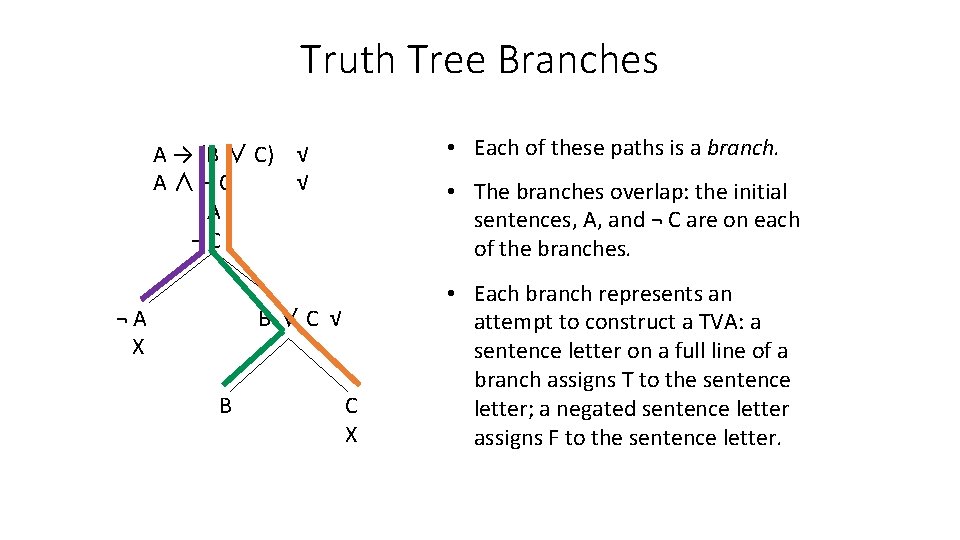
Or a Truth Tree • The truth tree systematically constructs the TVA in which all sentences are true if there is one and shows conclusively that there isn’t any such TVA if there isn’t one. • We list the sentence to be tested (the initial sentences) and, applying the Truth Tree Rules ‘decompose’ them into what it takes to make them true. • Each branch of the tree tries to represent a TVA that makes all initial sentences true. • If there is a TVA represented by growing the tree that makes all initial sentences true then the set of initial sentences is consistent. • If there isn’t then it’s inconsistent.

Behold, a Truth Tree! A → (B ∨ C) √ A∧¬C √ A ¬C Initial Sentences ¬A X B∨C √ B C X

Growing a Tree The tree rules and how to apply them to construct a truth tree

Growing a Tree • A truth tree for a set of WFFs is a structure that lists all the wffs, and all the wellformed components that must be true in attempting to show the set truthfunctionally consistent. • To grow a tree, rules are applied to the WFFs to produce a new WFFs that are written at the bottom of each branch that’s still growing (each ‘open’ branch) • Each of the rules ‘decomposes’ the WFF to which it was applied into components that make it true. • The Tree Rules (as we shall see) are read off from the characteristic truth tables for the connectives. • Each open branch (if any) on the finished tree represents a TVA that makes all initial sentences true.

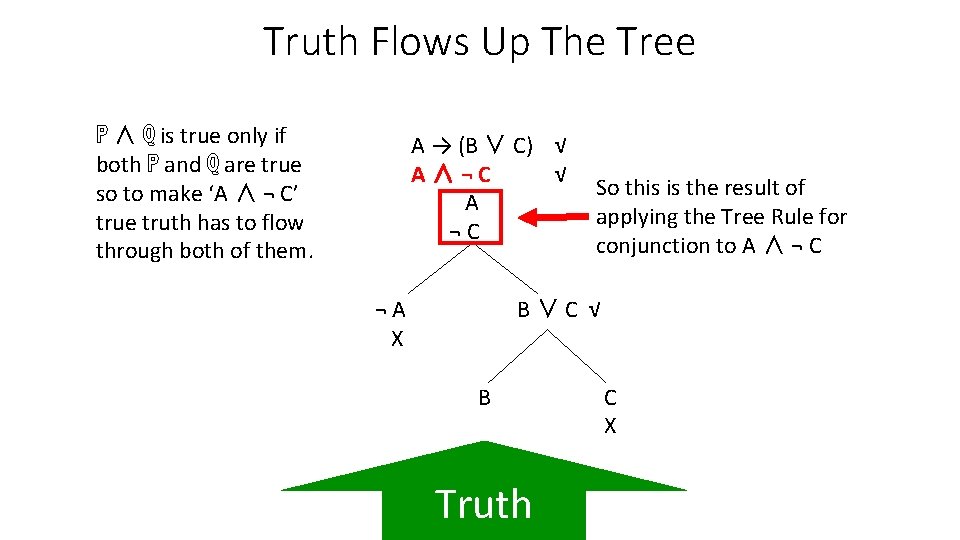
Truth Flows Up The Tree ℙ ∧ ℚ is true only if both ℙ and ℚ are true so to make ‘A ∧ ¬ C’ true truth has to flow through both of them. A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X So this is the result of applying the Tree Rule for conjunction to A ∧ ¬ C B∨C √ B Truth C X

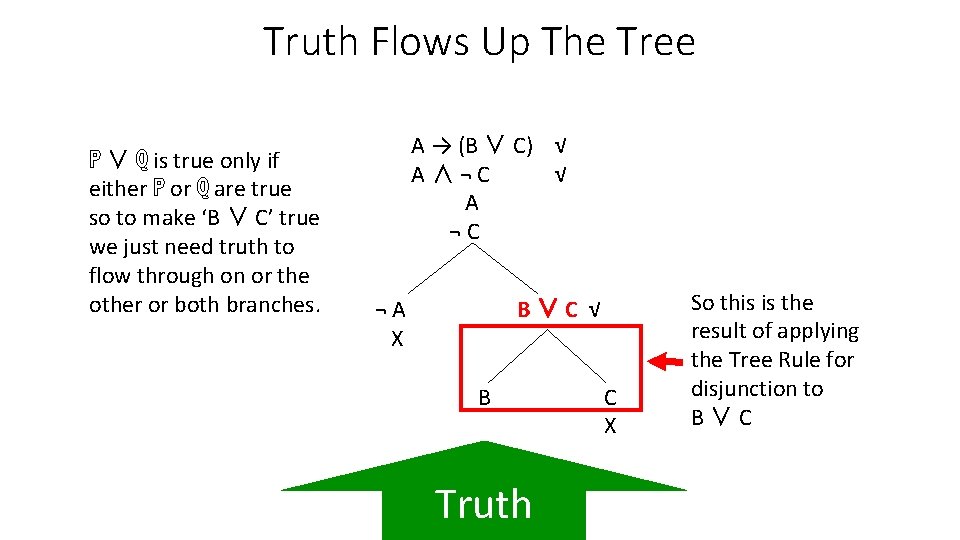
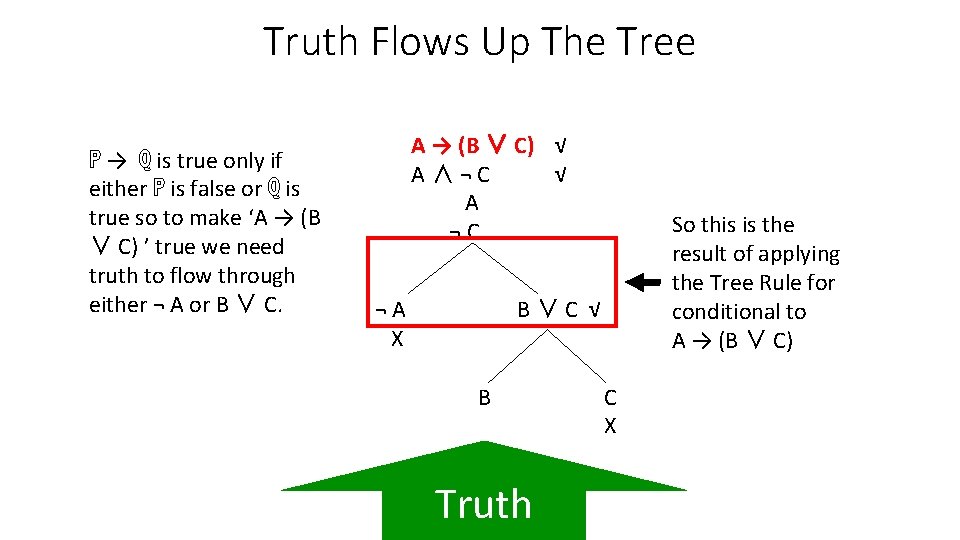
Truth Flows Up The Tree ℙ ∨ ℚ is true only if either ℙ or ℚ are true so to make ‘B ∨ C’ true we just need truth to flow through on or the other or both branches. A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X B∨C √ B Truth C X So this is the result of applying the Tree Rule for disjunction to B∨C


Series and Parallel Circuits

Logic Gates

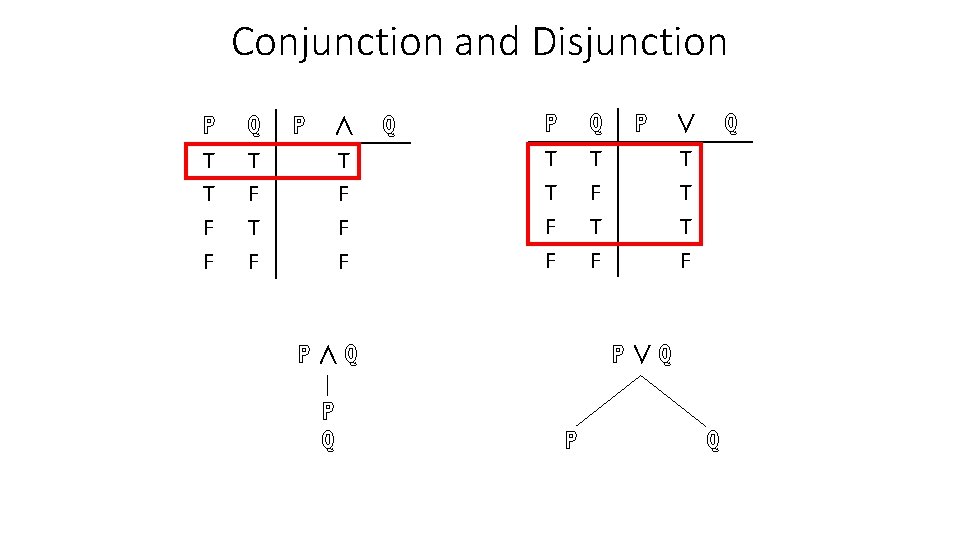
Branching and Non-Branching Rules ℙ T T F F Other rules are basically conjunctions or disfunctions ℚ T F ℙ ? T F F F ℙ? ℚ | ℙ ℚ ℚ ℙ T T F F ℚ T F ℙ ? T T T F ℚ ℙ? ℚ ℙ ℚ



Truth Flows Up The Tree ℙ → ℚ is true only if either ℙ is false or ℚ is true so to make ‘A → (B ∨ C) ’ true we need truth to flow through either ¬ A or B ∨ C. A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X So this is the result of applying the Tree Rule for conditional to A → (B ∨ C) B∨C √ B Truth C X


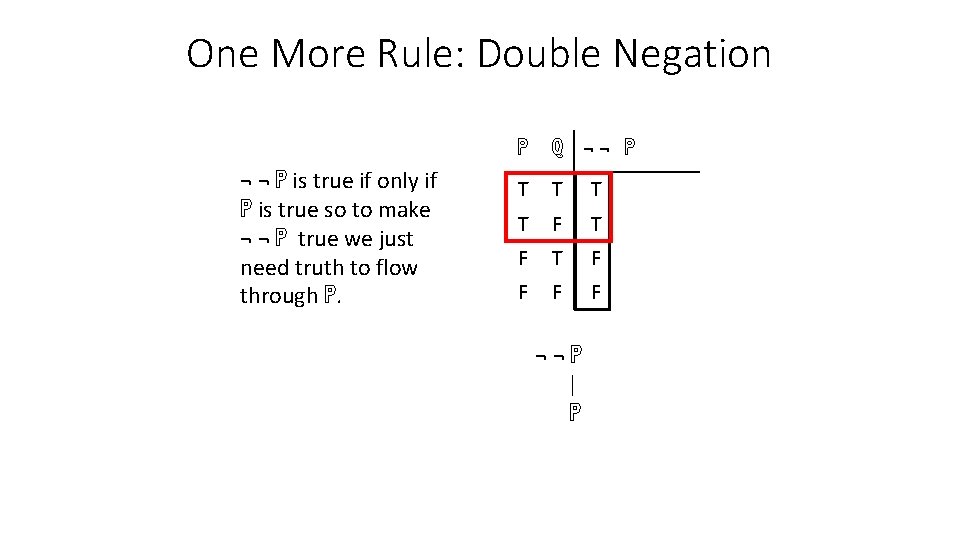
One More Rule: Double Negation ¬ ¬ ℙ is true if only if ℙ is true so to make ¬ ¬ ℙ true we just need truth to flow through ℙ. ℙ ℚ ¬¬ ℙ T T F T F F ¬¬ℙ | ℙ

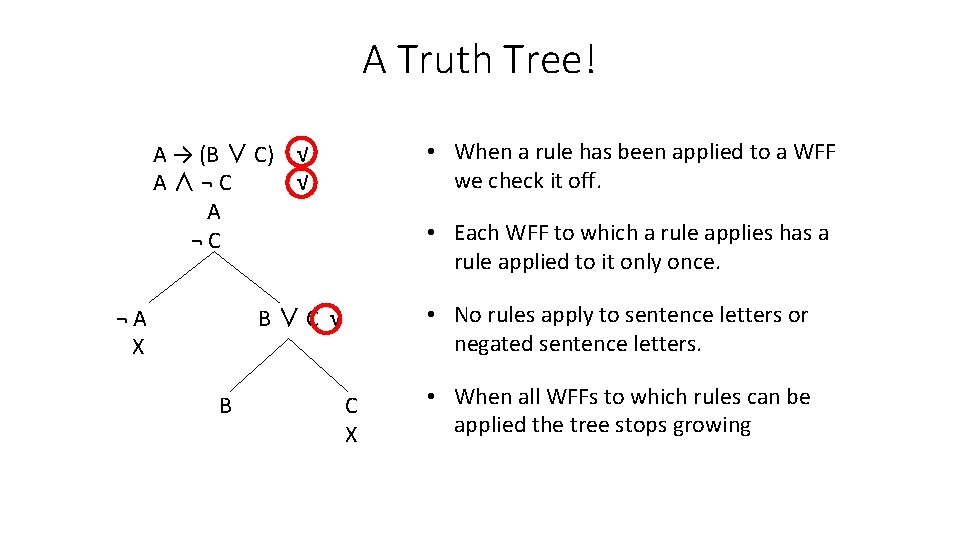
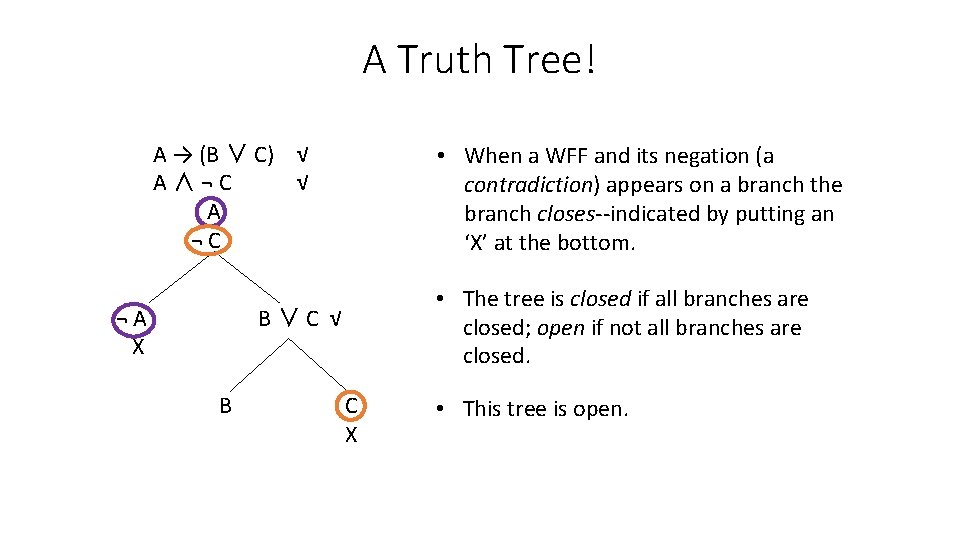
A Truth Tree! • When a rule has been applied to a WFF we check it off. A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X • Each WFF to which a rule applies has a rule applied to it only once. • No rules apply to sentence letters or negated sentence letters. B∨C √ B C X • When all WFFs to which rules can be applied the tree stops growing

Truth Tree Branches • Each of these paths is a branch. A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X • The branches overlap: the initial sentences, A, and ¬ C are on each of the branches. B∨C √ B C X • Each branch represents an attempt to construct a TVA: a sentence letter on a full line of a branch assigns T to the sentence letter; a negated sentence letter assigns F to the sentence letter.

A Truth Tree! A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X • When a WFF and its negation (a contradiction) appears on a branch the branch closes--indicated by putting an ‘X’ at the bottom. • The tree is closed if all branches are closed; open if not all branches are closed. B∨C √ B C X • This tree is open.

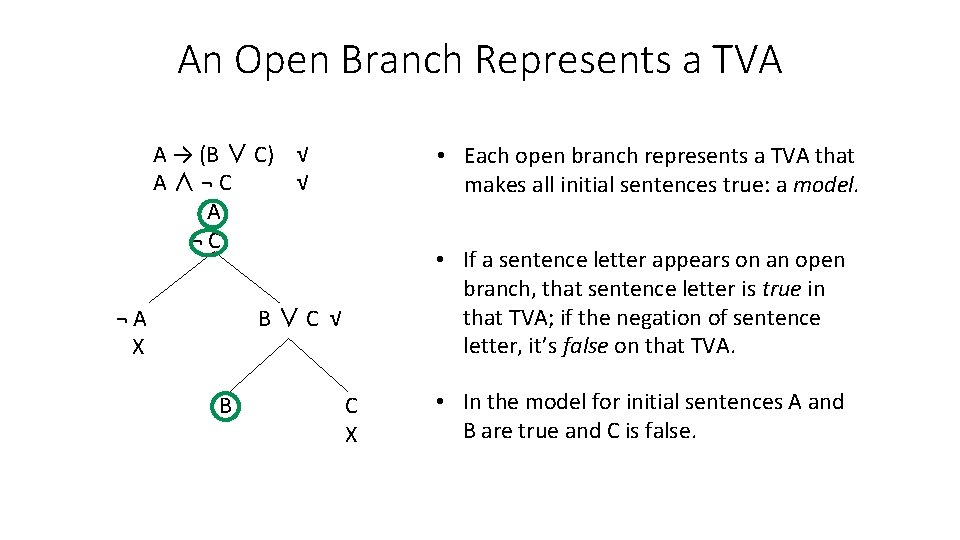
An Open Branch Represents a TVA A → (B ∨ C) √ A∧¬C √ A ¬C ¬A X • Each open branch represents a TVA that makes all initial sentences true: a model. • If a sentence letter appears on an open branch, that sentence letter is true in that TVA; if the negation of sentence letter, it’s false on that TVA. B∨C √ B C X • In the model for initial sentences A and B are true and C is false.

Truth Tree Tests Testing WFFs and sets of WFFs for semantic properties

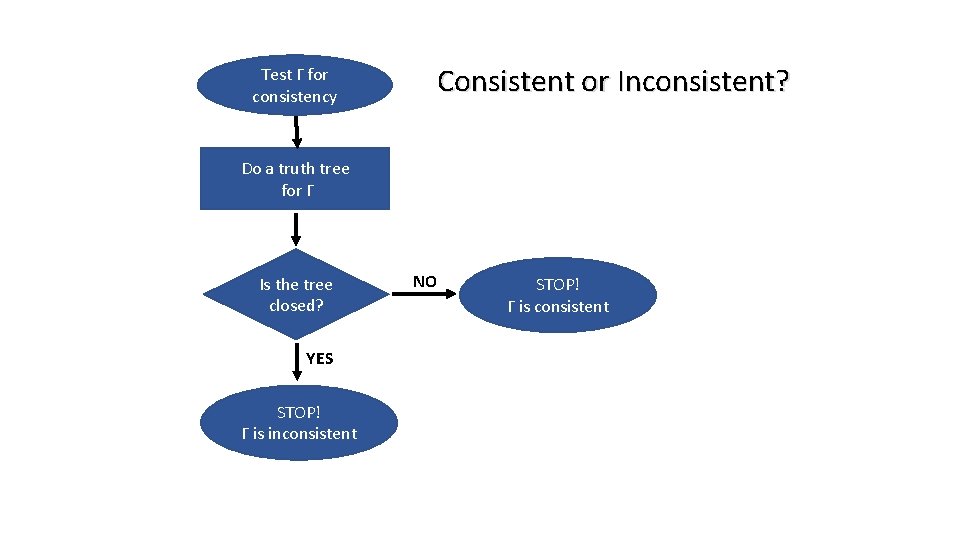
Truth Tree Tests • Consistency - A set Γ is truth-functionally consistent iff it has an open tree - A set Γ is truth functionally inconsistent iff it has a closed tree. • Tautologousness - A WFF ℙ is truth-functionally true (tautologous) iff {¬ ℙ} has a closed tree - WFF ℙ is truth functionally false (self-contradictory) iff {ℙ} has a closed tree - WFF ℙ is truth functionally contingent iff {ℙ} and {¬ ℙ} each has an open tree. • Satisfiability - A WFF ℙ is truth-functionally satisfiable iff {ℙ} has an open tree. - A WFF ℙ is truth-functionally falsifiable iff {¬ ℙ} has an open tree.

Consistent or Inconsistent? Test Γ for consistency Do a truth tree for Γ Is the tree closed? YES STOP! Γ is inconsistent NO STOP! Γ is consistent

The Consistency Test A→B √ B→C √ A∧¬C√ A ¬C Q&A • Q: What are the initial sentences? • A: A → B, B → C, and A ∧ ¬ C • Q: What truth-value assignment, if any, makes all the initial sentences true? • A: The initial sentences are inconsistent, so NO truth value assignment makes all sentences true! ¬A X B ¬B X Inconsistent C X

The Consistency Test Q&A • Q: What are the initial sentences? • A: E ∧ ¬ G, E → ¬ ¬ C, and ¬ (C → B) • Q: What truth-value assignment, if any, makes all the initial sentences true? • A: E – true, B – false, C - true Consistent

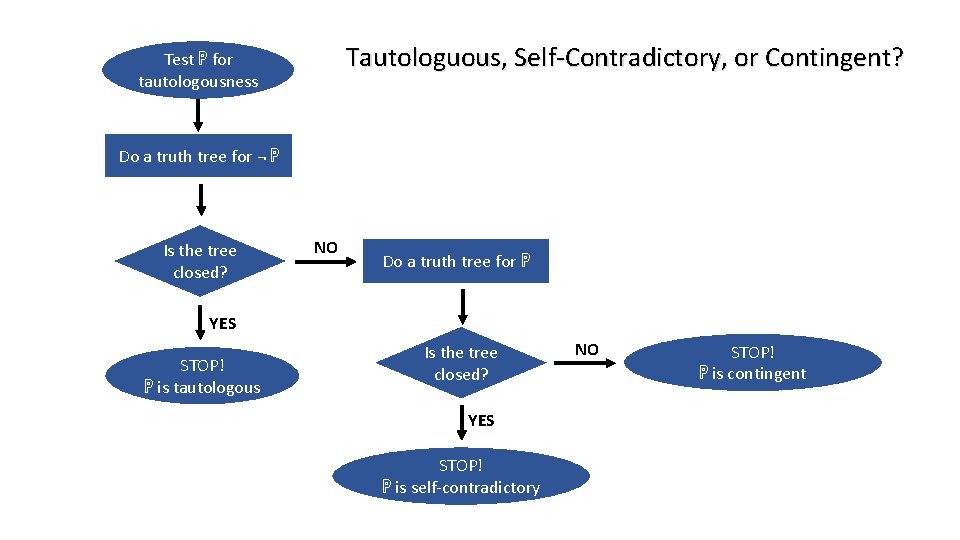
Tautologuous, Self-Contradictory, or Contingent? Test ℙ for tautologousness Do a truth tree for ¬ ℙ Is the tree closed? NO Do a truth tree for ℙ YES STOP! ℙ is tautologous Is the tree closed? YES STOP! ℙ is self-contradictory NO STOP! ℙ is contingent

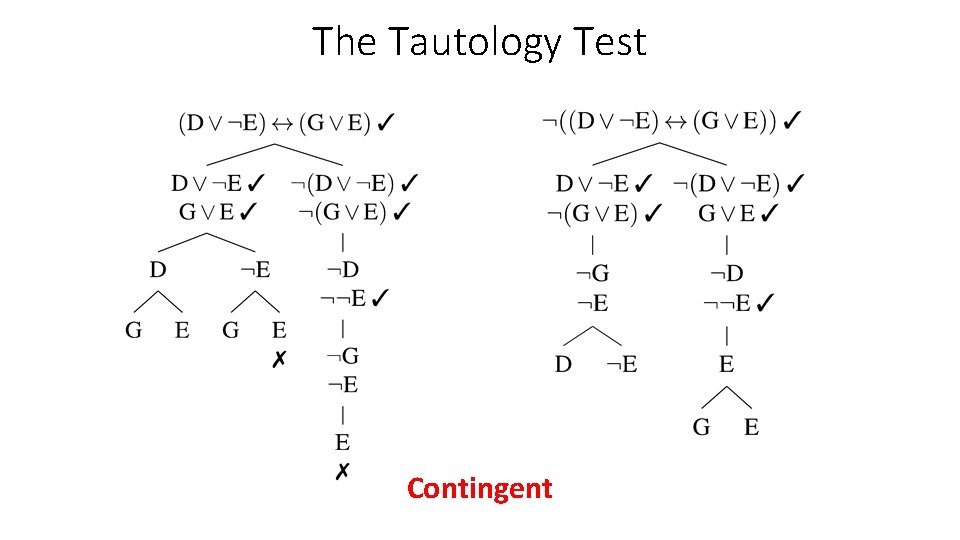
The Tautology Test Q&A • Q: What sentence is being tested? • A: (A ∧ B) → ((¬ A ∨ B) → C) • Q: Is it tautologous (truth-functionally true), self-contradictory (truthfunctionally false) or contingent? • A: Tautogogous Tautologous
![The Tautology Test A B A B The Tautology Test ¬ [(A → B) ∧ ¬ (¬ A ∨ B)] √](https://slidetodoc.com/presentation_image_h2/b0816fceddf95d927b062c0842b1fd01/image-32.jpg)
The Tautology Test ¬ [(A → B) ∧ ¬ (¬ A ∨ B)] √ (A → B) A ¬B ¬ (¬ A ∨ B)] ¬¬A ¬B A (A → B) ∧ ¬ (¬ A ∨ B)] √ (A → B) ¬ (¬ A ∨ B)] ¬¬A ¬B A ¬A X B X • Testing the negation of the sentence (left) shows the sentence could be false. • Testing the sentence itself (right) shows it can’t be true, so self-contradictory. • Correct—but could have saved work beginning with test of sentence itself!

The Tautology Test Contingent

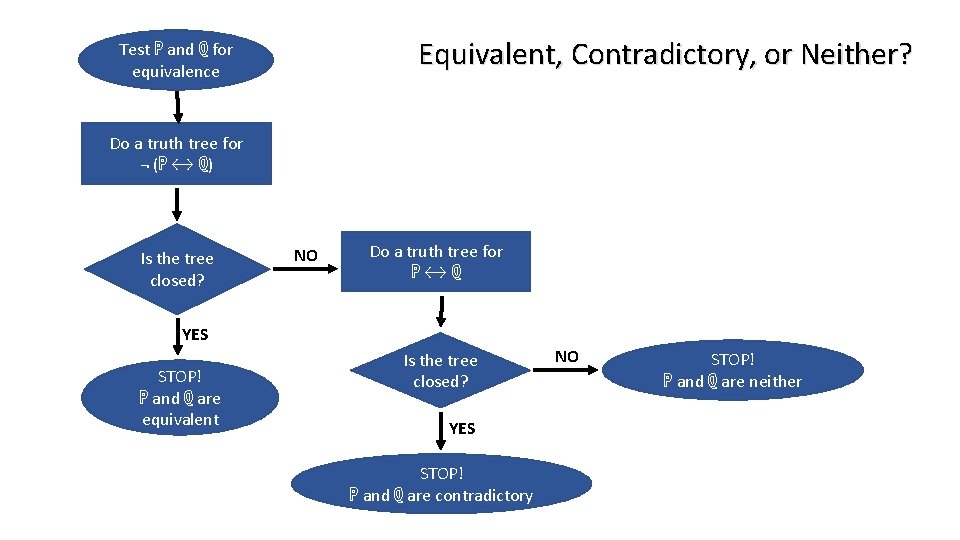
Equivalent, Contradictory, or Neither? Test ℙ and ℚ for equivalence Do a truth tree for ¬ (ℙ ↔ ℚ) Is the tree closed? NO Do a truth tree for ℙ↔ℚ YES STOP! ℙ and ℚ are equivalent Is the tree closed? YES STOP! ℙ and ℚ are contradictory NO STOP! ℙ and ℚ are neither

The Equivalence Test Note: sentences that were being tested for equivalence were: I → ¬ J and ¬ J ∨ ¬ I Biconditional shows equivalence: ℙ is equivalent to ℚ iff ℙ ↔ ℚ is tautologous. So we test ‘(I → ¬ J) ↔ (¬ J ∨ ¬ I)’ for tautologousness. Equivalent

The Equivalence Test Neither Equivalent nor Contradictory

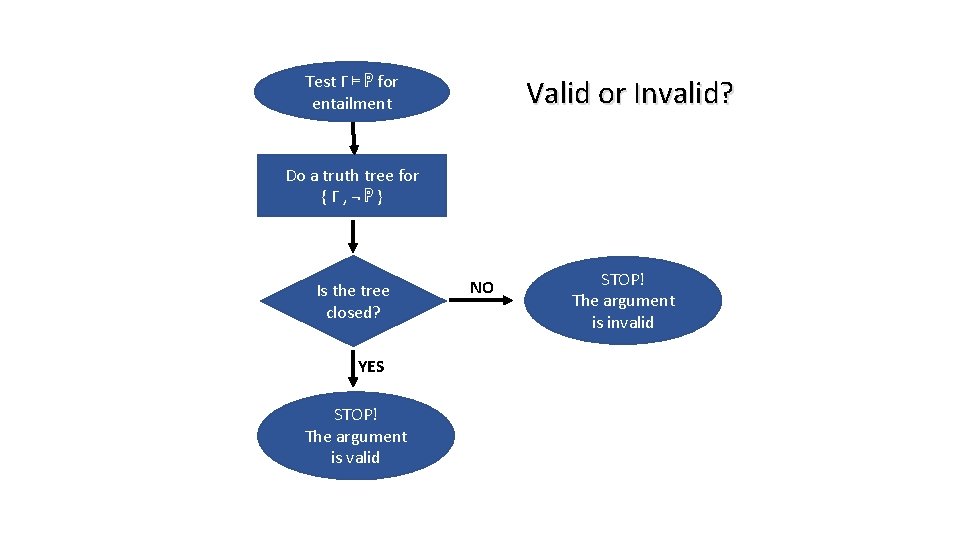
Truth Functional Entailment & Validity • A set of WFFs, Γ , truth-functionally entails a target WFF, ℙ, iff Γ together with ¬ ℙ has a closed tree. • An argument is truth-functionally valid iff the set consisting of all and only the premises and the negation of the conclusion has a closed tree. • Entailment and Validity - An argument is valid iff its premises entail its conclusion. - An argument is valid iff the set of sentences consisting of its premises and the negation of its conclusion is inconsistent, that is… - There’s no TVA that makes all its premises true and its conclusion false.

Test Γ ⊨ ℙ for entailment Valid or Invalid? Do a truth tree for {Γ, ¬ℙ} Is the tree closed? YES STOP! The argument is valid NO STOP! The argument is invalid

The Validity Test Q&A • Q: What is the conclusion of this argument? • A: ‘A’, because its negation, ‘¬ A’ is the last of the initial sentences. • Q: What truth value assignment(s), if any makes all initial sentences true? • A: A – false, B – false, C – true and A – false, B – true, C – true

The Validity Test Q&A • Q: What is the conclusion of this argument? • A: ‘¬ D → (B ∨ C)’, because its negation, ‘¬(¬D → (B ∨ C)’, is the last of the initial sentences. • Q: What truth value assignment(s), if any makes all initial sentences true? • A: A – false, B – false, C – true and A – false, B – true, C – true

The Validity Test: What Went Wrong This stuff shouldn’t be here because… There is a contradiction on the rightmost branch! So the branch should have stopped growing… X …and there should be an X beneath the ‘D’ at the bottom of the branch.

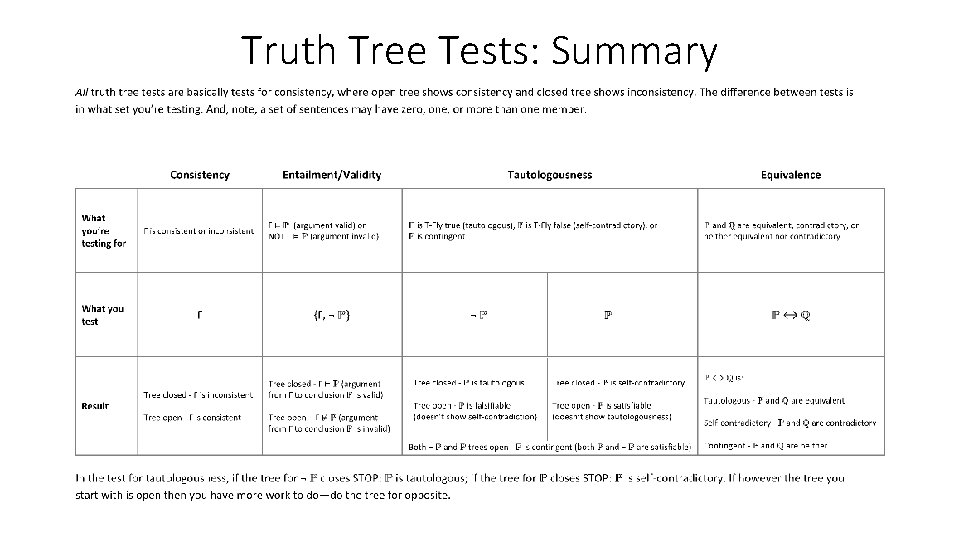
Truth Tree Tests: Summary

3. 5. 2 Exercises: Test for Tautologousness
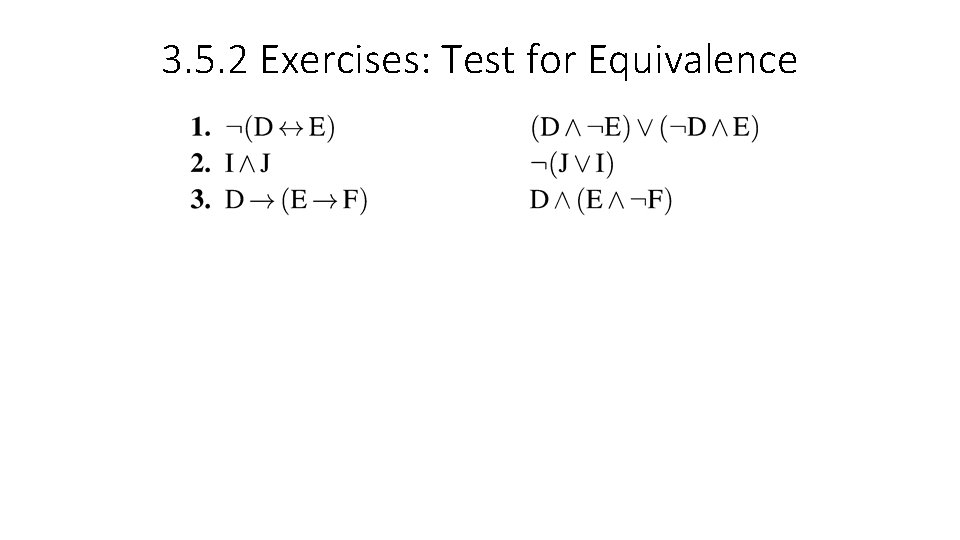
3. 5. 2 Exercises: Test for Equivalence

Test for Validity

The End