3 5 Perform Basic Matrix Operations A Matrix

3. 5 Perform Basic Matrix Operations

A Matrix • Is a rectangular arrangement of elements in rows and columns. The elements in a matrix are called it’s entries.

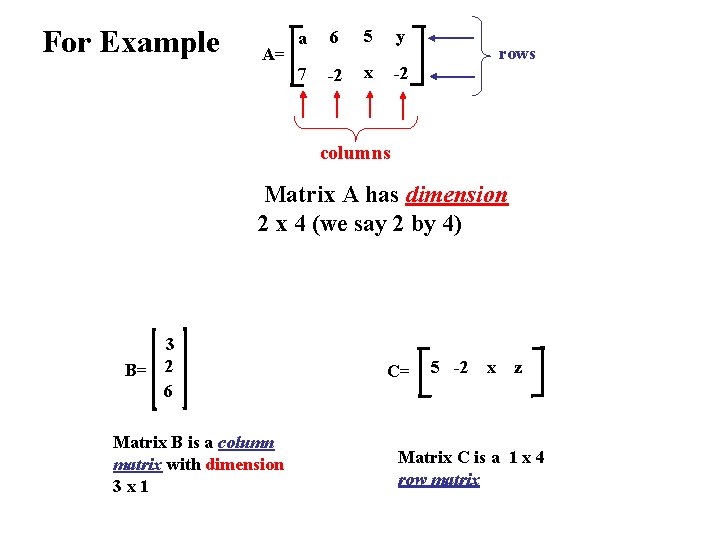
For Example A= a 6 5 y 7 -2 x -2 rows columns Matrix A has dimension 2 x 4 (we say 2 by 4) 3 B= 2 6 Matrix B is a column matrix with dimension 3 x 1 C= 5 -2 x z Matrix C is a 1 x 4 row matrix

A square Matrix has the same number of rows and columns. A matrix whose entries are all zeros is called the Zero Matrix. Two matrices are equal if their dimensions are the same and the entries in corresponding positions are equal.

A= Z 5 4 -3 B= Z 5 4 -3 Matrix A and matrix B are both 2 x 2 and have the same elements in the same corresponding entries, so they are equal. C= 3 4 f z 7 -9 s -2 4 D= 2 1 Are matrices C and D equal? No, they have different number of columns and rows and different elements.

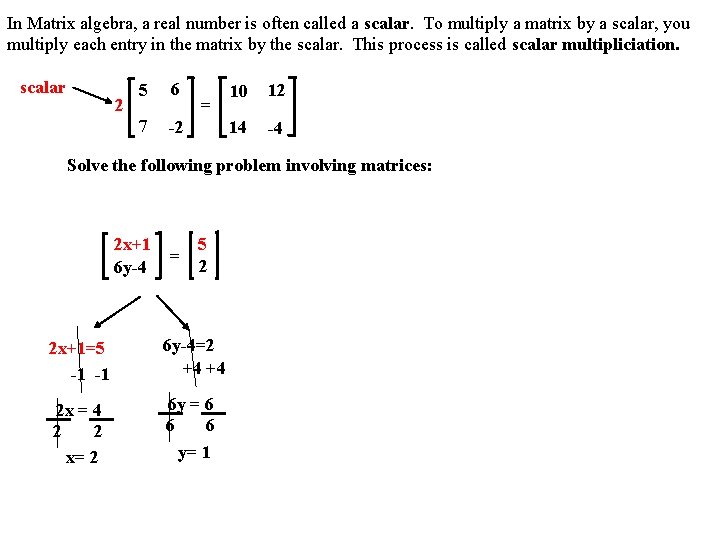
In Matrix algebra, a real number is often called a scalar. To multiply a matrix by a scalar, you multiply each entry in the matrix by the scalar. This process is called scalar multipliciation. scalar 2 5 6 7 -2 = 10 12 14 -4 Solve the following problem involving matrices: 2 x+1 6 y-4 = 5 2 2 x+1=5 -1 -1 6 y-4=2 +4 +4 2 x = 4 2 2 x= 2 6 y = 6 6 6 y= 1

We can do Matrix Arithmetic like ADDITION or Subtraction 2 3 -2 4 2 3 -2 5 7 6 8 2 4 7 2 1 + - + 4 6 7 1 0 2+4 = -2+7 10 = 10 2 3 6 -2 7 -7 = 3+6 5+10 8 -4 2 -10 6 -4 = 7 -4 8 = 6 9 5 = 4 4 0 2 15 + -8 1 0 2 3 10 5 Notice that matrices that are added or subtracted have the same dimensions.