3 5 Graphing Linear Equations in Three Variables

3. 5 Graphing Linear Equations in Three Variables

A Global Positioning System (GPS) gives locations using the three coordinates of latitude, longitude, and elevation. You can represent any location in threedimensional space using a three-dimensional coordinate system, sometimes called coordinate space.

Each point in coordinate space can be represented by an ordered triple of the form (x, y, z). The system is similar to the coordinate plane but has an additional coordinate based on the z-axis. Notice that the axes form three planes that intersect at the origin.

Helpful Hint To find an intercept in coordinate space, set the other two coordinates equal to 0.

Example: Graphing Points in Three Dimensions Graph the point in three-dimensional space. A(3, – 2, 1) z From the origin, move 3 units forward along the x-axis, 2 units left, and 1 unit up. y A(3, – 2, 1) x

Example: Graphing Points in Three Dimensions Graph the point in three-dimensional space. B(2, – 1, – 3) z From the origin, move 2 units forward along the x-axis, 1 unit left, and 3 units down. y x B(2, – 1, – 3)

Example: Graphing Points in Three Dimensions Graph the point in three-dimensional space. C(– 1, 0, 2) z From the origin, move 1 unit back along the x-axis, 2 units up. Notice that this point lies in the xz-plane because the y-coordinate is 0. C(– 1, 0, 2) y x

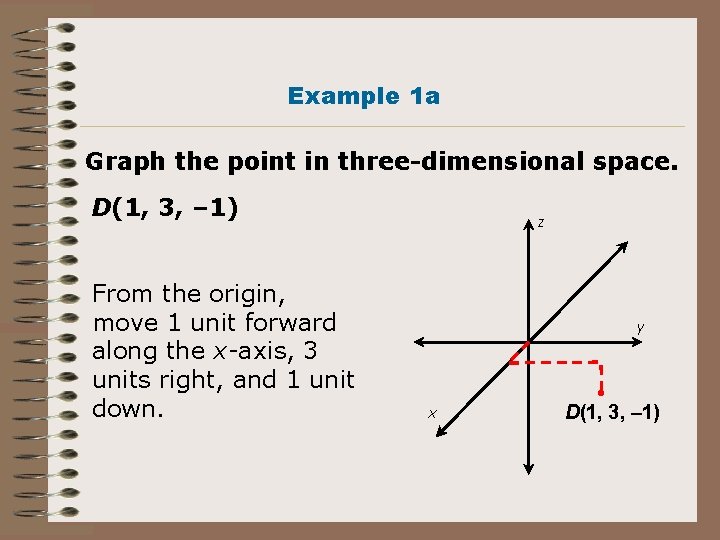
Example 1 a Graph the point in three-dimensional space. D(1, 3, – 1) From the origin, move 1 unit forward along the x-axis, 3 units right, and 1 unit down. z y x D(1, 3, – 1)

Example 1 b Graph the point in three-dimensional space. E(1, – 3, 1) z From the origin, move 1 unit forward along the x -axis, 3 units left, and 1 E(1, – 3, 1) unit up. x y

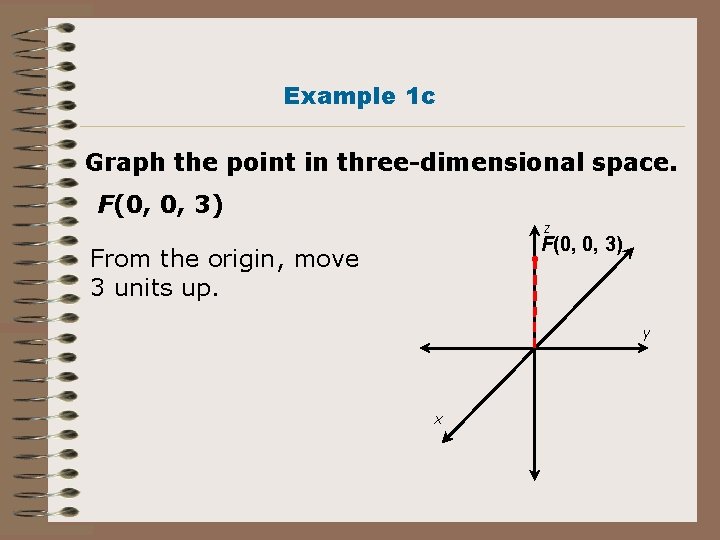
Example 1 c Graph the point in three-dimensional space. F(0, 0, 3) z From the origin, move 3 units up. F(0, 0, 3) y x

Recall that the graph of a linear equation in two dimensions is a straight line. In threedimensional space, the graph of a linear equation is a plane. Because a plane is defined by three points, you can graph linear equations in three dimensions by finding the three intercepts.

Example 2: Graphing Linear Equations in Three Dimensions Graph the linear equation 2 x – 3 y + z = – 6 in three-dimensional space. Step 1 Find the intercepts: x-intercept: 2 x – 3(0) + (0) = – 6 x = – 3 y-intercept: 2(0) – 3 y + (0) = – 6 y=2 z-intercept: 2(0) – 3(0) + z = – 6

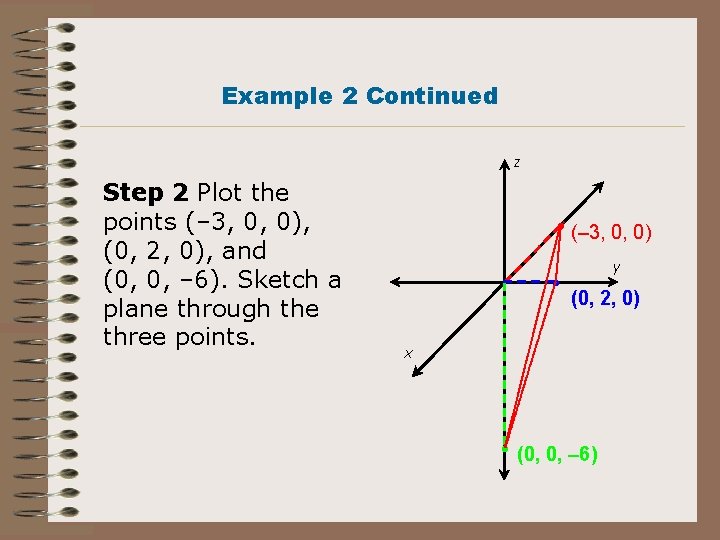
Example 2 Continued z Step 2 Plot the points (– 3, 0, 0), (0, 2, 0), and (0, 0, – 6). Sketch a plane through the three points. (– 3, 0, 0) y (0, 2, 0) x (0, 0, – 6)

Example 2 Graph the linear equation x – 4 y + 2 z = 4 in three-dimensional space. Step 1 Find the intercepts: x-intercept: x – 4(0) + 2(0) = 4 x=4 y-intercept: (0) – 4 y + 2(0) = 4 y = – 1 z-intercept: (0) – 4(0) + 2 z = 4 z=2

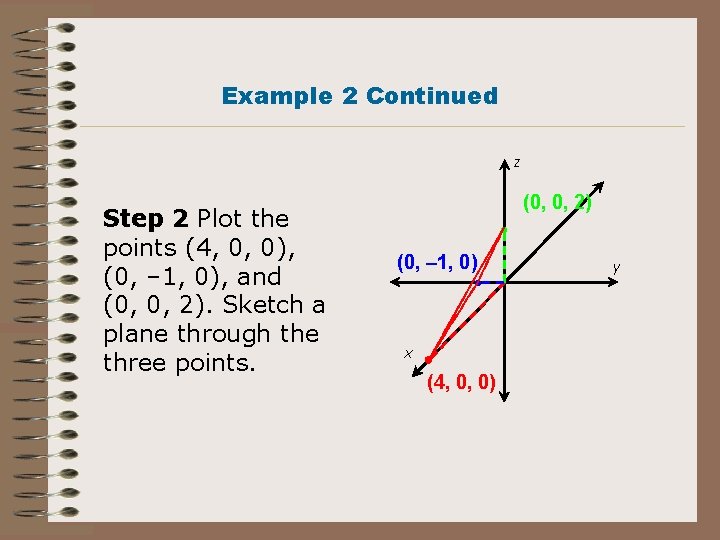
Example 2 Continued z Step 2 Plot the points (4, 0, 0), (0, – 1, 0), and (0, 0, 2). Sketch a plane through the three points. (0, 0, 2) (0, – 1, 0) x ● (4, 0, 0) y

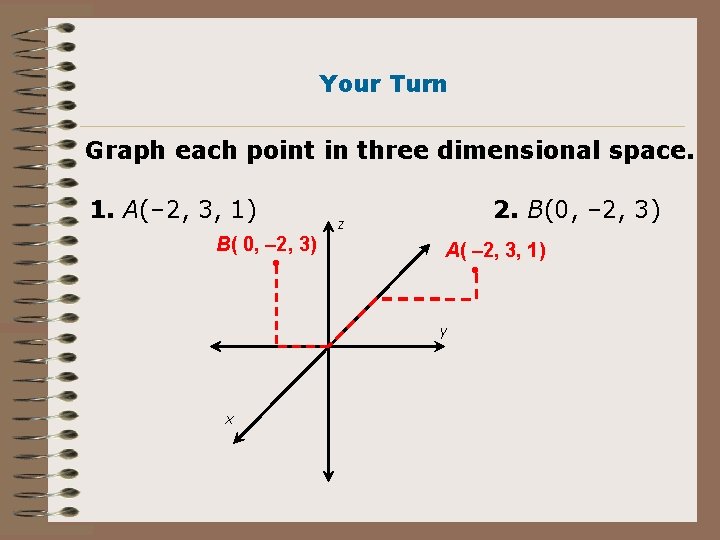
Your Turn Graph each point in three dimensional space. 1. A(– 2, 3, 1) 2. B(0, – 2, 3) z B( 0, – 2, 3) A( – 2, 3, 1) y x

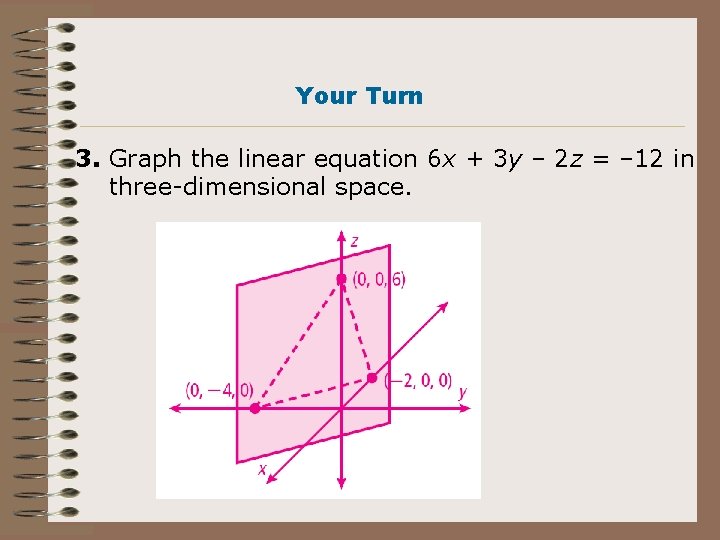
Your Turn 3. Graph the linear equation 6 x + 3 y – 2 z = – 12 in three-dimensional space.