3 4 Transformations of Graphs Graph functions using










- Slides: 15

3. 4 Transformations of Graphs ♦ Graph functions using vertical and horizontal translations ♦ Graph function using stretching and shrinking ♦ Graph function using reflections ♦ Combine transformations Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

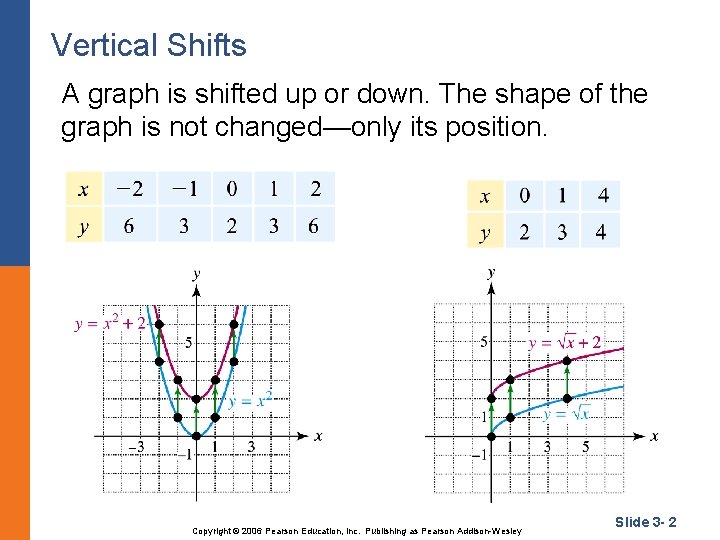
Vertical Shifts A graph is shifted up or down. The shape of the graph is not changed—only its position. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 2

Horizontal Shifts A graph is shifted left or right. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 3

Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 4

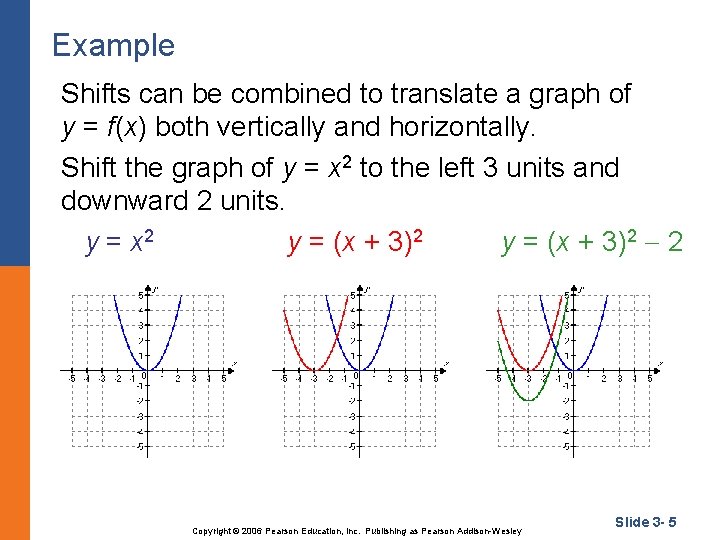
Example Shifts can be combined to translate a graph of y = f(x) both vertically and horizontally. Shift the graph of y = x 2 to the left 3 units and downward 2 units. y = x 2 y = (x + 3)2 2 Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 5

Example Find an equation that shifts the graph of f(x) = x 2 2 x + 3 left 4 units and down 3 units. Solution Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 6

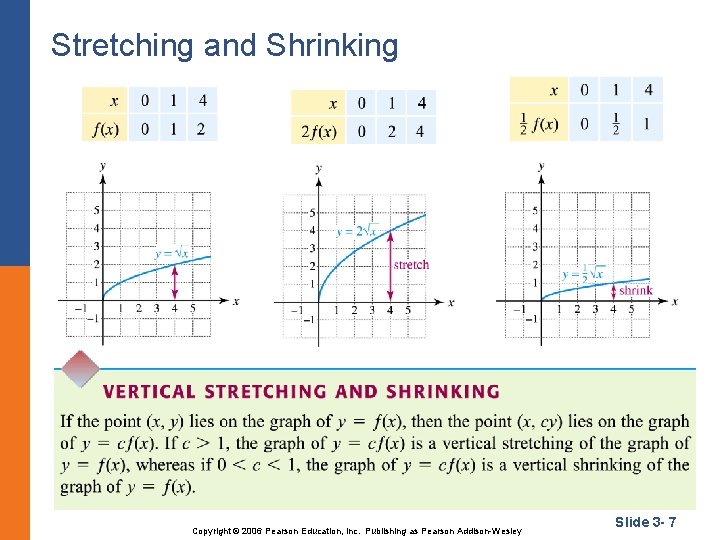
Stretching and Shrinking Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 7

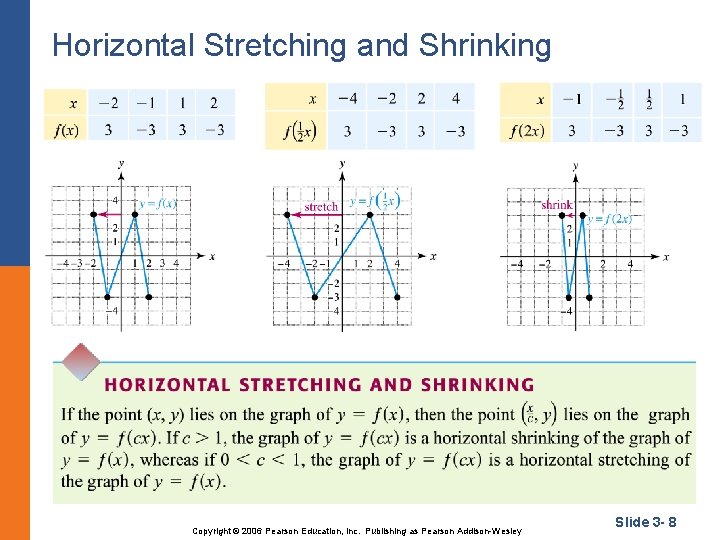
Horizontal Stretching and Shrinking Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 8

Example Use the graph of y = f(x) to sketch the graph of each equation. a) y = 2 f(x) b) Solution Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 9

Solution continued b) Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 10

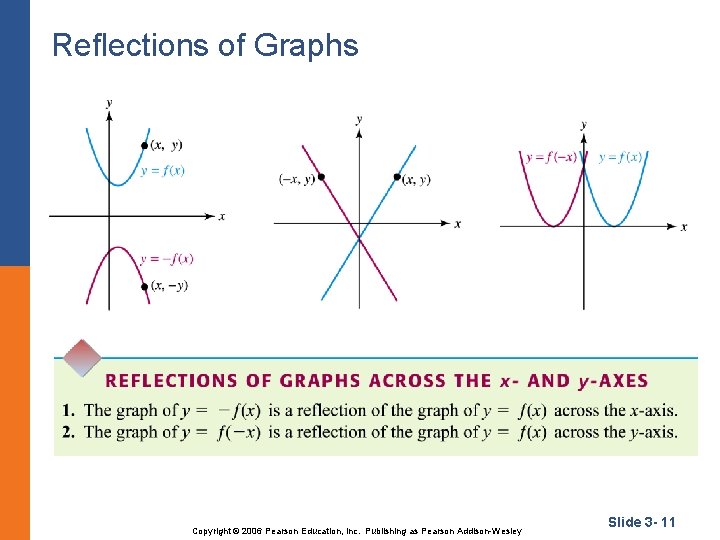
Reflections of Graphs Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 11

Example For the function f(x) = x 2 + x 2 graph its reflection across the x-axis and across the y-axis. Solution Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 12

Combining Transformations of graphs can be combined to create new graphs. For example the graph of y = 3(x + 3)2 + 1 can be obtained by performing four transformations on the graph of y = x 2. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 13

Combining Transformations continued y = 3(x + 2 3) +1 Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 14

Example Describe how the graph of the equation can be obtained by transforming the graph of y = |x|. Then graph the equation. Solution Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 15