3 4 The Fundaemental Theorem of Algebra and

3. 4 – The Fundaemental Theorem of Algebra and Graph Sketching Section 3. 4

Domain and range The domain and range will be examined further in later lessons. For the purpose of this slide you may assume that: Domain is the x-values of a function or graph (input). Range is the y-values of a function or graph (output).

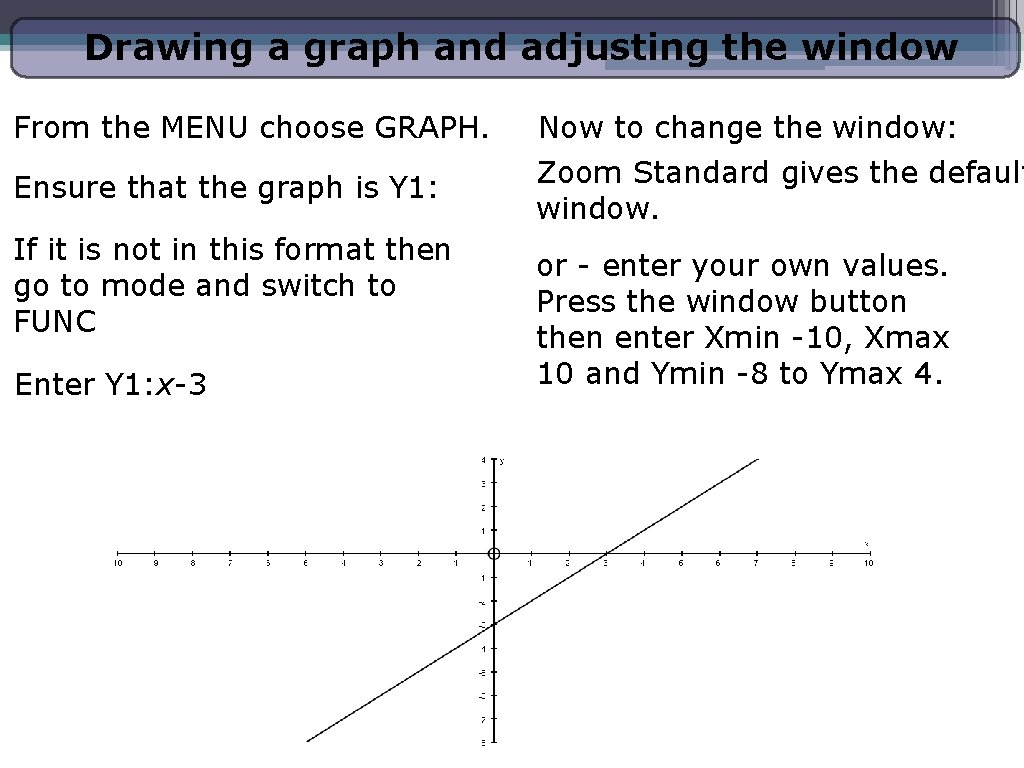
Drawing a graph and adjusting the window From the MENU choose GRAPH. Ensure that the graph is Y 1: If it is not in this format then go to mode and switch to FUNC Enter Y 1: x-3 Now to change the window: Zoom Standard gives the default window. or - enter your own values. Press the window button then enter Xmin -10, Xmax 10 and Ymin -8 to Ymax 4.

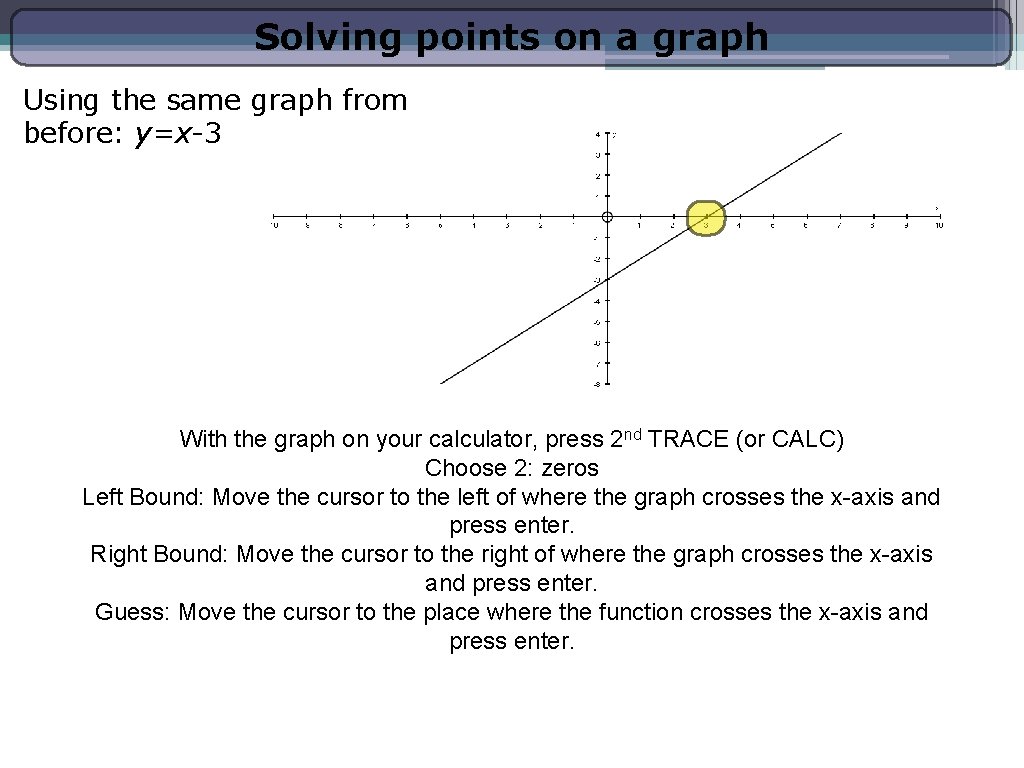
Solving points on a graph Using the same graph from before: y=x-3 With the graph on your calculator, press 2 nd TRACE (or CALC) Choose 2: zeros Left Bound: Move the cursor to the left of where the graph crosses the x-axis and press enter. Right Bound: Move the cursor to the right of where the graph crosses the x-axis and press enter. Guess: Move the cursor to the place where the function crosses the x-axis and press enter.

More solving points on a graph Now for a quadratic: 1. Enter this quadratic and get a window so that you can see all the information needed. 2. Find both roots. Use the cursor key for the second root. x=-4 and x=7 3. Find the minimum coordinates. 5. Find f(4) (using GDC). y=-24 4. Find the y-intercept. y=-28 6. Find f(x)=5 (using GDC). x=-4. 44

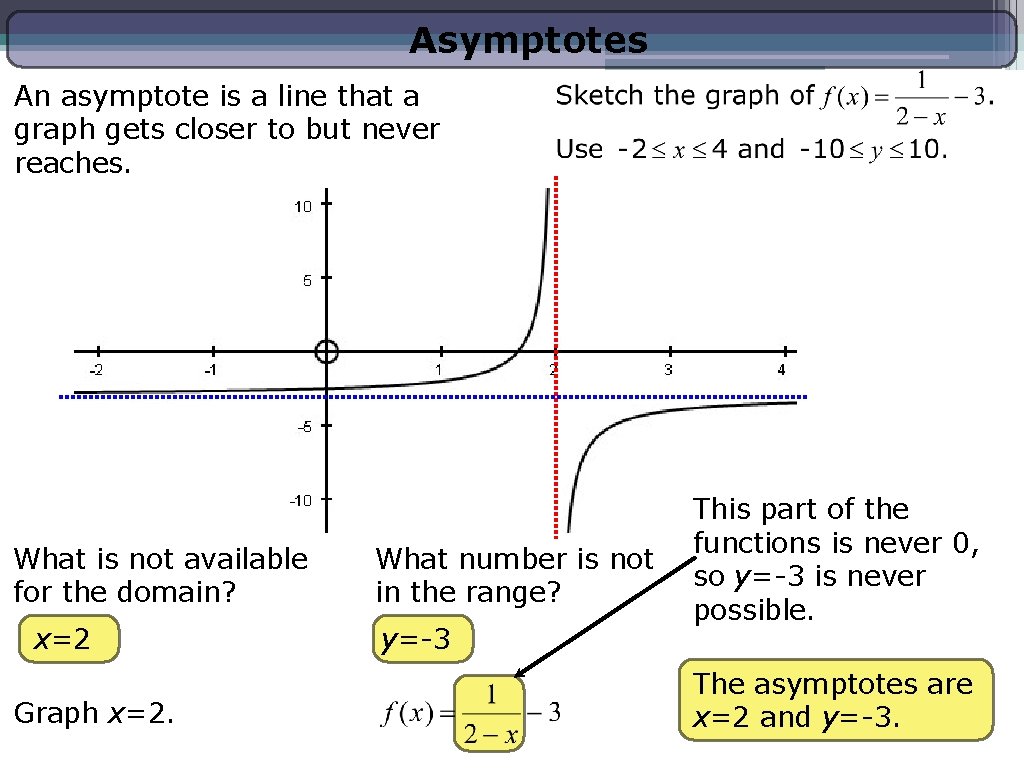
Asymptotes An asymptote is a line that a graph gets closer to but never reaches. What is not available for the domain? x=2 Graph x=2. What number is not in the range? y=-3 This part of the functions is never 0, so y=-3 is never possible. The asymptotes are x=2 and y=-3.

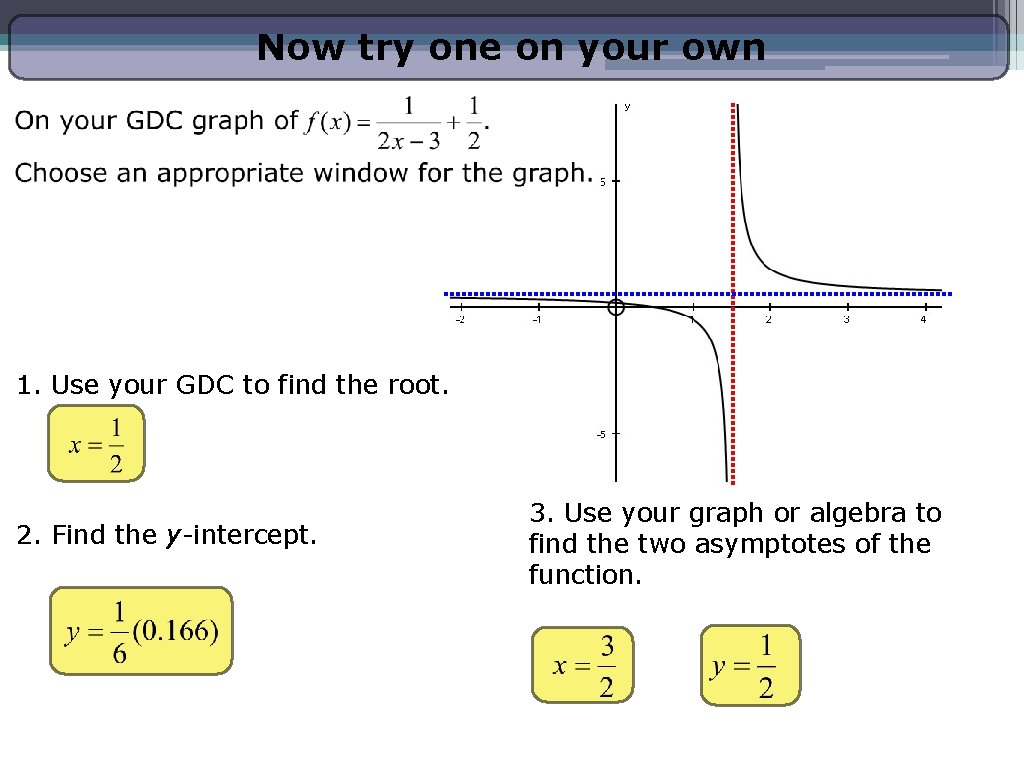
Now try one on your own 1. Use your GDC to find the root. 2. Find the y-intercept. 3. Use your graph or algebra to find the two asymptotes of the function.

Information about sketching graphs You may be asked to sketch a graph. This is usually after you have used a GDC, but not always. A sketch does not need to be accurate, but it does need to be neat and it must show the vital information. You will not need graph paper. Your sketch should be: • • • about a third of a page in size, drawn in pencil with a ruler for all the straight lines including the axes, clearly labeled, this includes the axes. On your sketch you must mark the following points: • where the graph intercepts the axes, • draw and label the asymptotes.

Understanding Rational Functions and Their Graphs • Finding y-intercepts ▫ There will only be one y-int. If there is more, it is not a function! ▫ To find the y-int, plug in 0 for all x ▫ Eg. , the y-int will be at y = -3 or (0, -3) • Finding x-intercepts ▫ The only way to get an x-int is when y = 0 ▫ The only way for y = 0 is when the numerator = 0 ▫ Take the numerator, set it equal to 0, solve for x ▫ Eg. , so the x-intercept is at ▫ Note: There can be more than one x-int

Understanding Rational Functions and Their Graphs Part 2 • Finding maximums/minimums (once you learn calculus) ▫ Take the first derivative and set equal to zero ▫ Factor and solve to get x coordinates ▫ Plug x’s into the original equation to get the y coordinates ▫ Eg. So y’ will equal 0 only when the numerator equals 0, so x equal +/- 2 so the coordinates are (2, . 25) and (-2, -. 25) • Finding Holes ▫ Holes occur when a binomial cancels out of an equation ▫ Find the part that cancels and set equal to 0, and solve for x ▫ Eg. , but x + 2 = 0, x = -2, so the line y = x – 2 has a hole at x = -2

Understanding Rational Functions and Their Graphs Part 3 • Finding Vertical Asymptotes ▫ Canceling should be done first ▫ Take the denominator, set equal to 0 and solve for x ▫ There may be several vertical asymptotes ▫ Eg. , a hole at x = -2, vertical asymptotes at x = -3 and x = 4 • Finding Horizontal Asymptotes ▫ Case 1: Numerator degree < Denominator degree The x-axis (y = 0) is the asymptote Eg. , horizontal asymptote at y = 0 ▫ Case 2: Numerator degree = Denominator degree The fraction formed by the leading coefficients is the asymptote Eg. , leading coefficients are so there is a horizontal asymptote at y = 2

Understanding Rational Functions and Their Graphs Part 4 ▫ Case 3: Numerator degree > Denominator degree No horizontal asymptote, instead it is oblique To find the exact equation, do long division, ignoring the remainder. Eg. , oblique asymptote at Note: Oblique asymptotes can be curves and graphs may cross obliques in the middle. End behavior follows the asymptote as usual, getting closer and closer without touching ▫ Note: With rational functions there is at most one horizontal asymptote.

Understanding Rational Functions and Their Graphs Part 5 • Steps to getting a graph Graph the vertical and horizontal asymptotes first. Find x and y intercepts Plot stationary points (and inflection points if needed, once you learn calculus) If you still do not have a clear picture, plot several points in each region and on both sides of the stationary points. Sketch in a graph, leaving out holes.

For each equation in this section give the domain and range and the equations of the vertical and horizontal asymptote(s). Find the x and y intercepts then sketch a graph. 1. . 2. . 3. . 4. .

For each equation in this section find the oblique asymptote, vertical asymptote(s), and the x and y intercepts then make a sketch of the graph. 1. . 2. . 3. .

For each equation in this section identify any holes in the graph, find vertical, horizontal or oblique asymptote(s) and sketch the graph. 1. . 2. . 3. .

Fundamental theorem of algebra • If f(x) is a polynomial, Then there will be at least one real or complex zero. Corollary: If f(x) has a degree of n, there will be n zeros. These zeros may be real, imaginary, different numbers or the same number multiple times.

Conjugate Root Theorem • If a + bi is a root then a – bi must also be a root

Sum and Product of Polynomial Roots • For a polynomial, f(x) of degree n with roots x 1, x 2, x 3, …, xn and f(x) = axn + bxn-1 + cx(n-2)… • X 1+x 2+x 3+…+ xn = -b/a • X 1 x 2 + x 2 x 3 + x 3 x 1 + … = c/a • X 1 x 2 x 3 +x 1 x 2 x 4 + … = -d/a. . .

Example • Let f(x)= ax 3 + bx 2 + cx + d and it has roots of X 1, X 2 and X 3 • X 1+X 2+X 3 = -b/a • X 1 X 2 +X 2 X 3 + X 3 X 1 = c/a • X 1 X 2 X 3 =-d/a