3 4 Limits Involving Infinity Horizontal Asymptotes Vertical

3. 4 Limits Involving Infinity Horizontal Asymptotes Vertical Asymptotes

Limits as ‘ x ’ Approaches Infinity At times you’ll need to know the behavior of a function or an expression as the inputs get increasingly larger in the positive and negative directions. We can evaluate this using the limit: Obviously, you cannot use direct substitution when it comes to these limits. Infinity is not a number, but a way of denoting how the inputs for a function can grow without any bound. 2

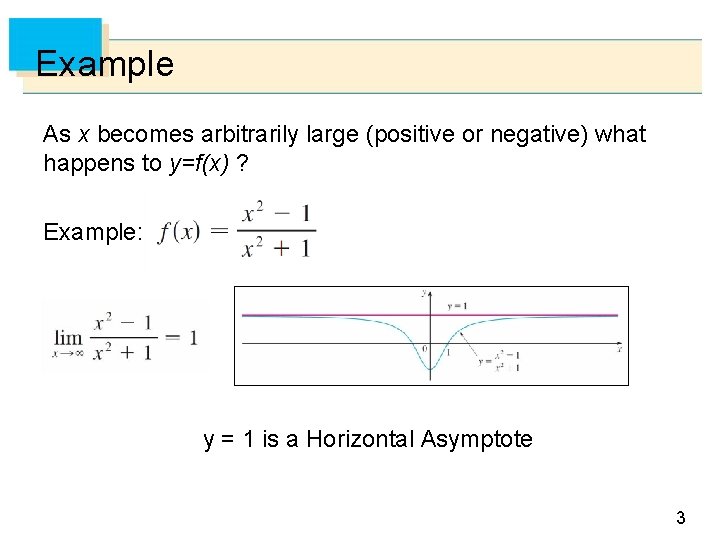
Example As x becomes arbitrarily large (positive or negative) what happens to y=f(x) ? Example: y = 1 is a Horizontal Asymptote 3

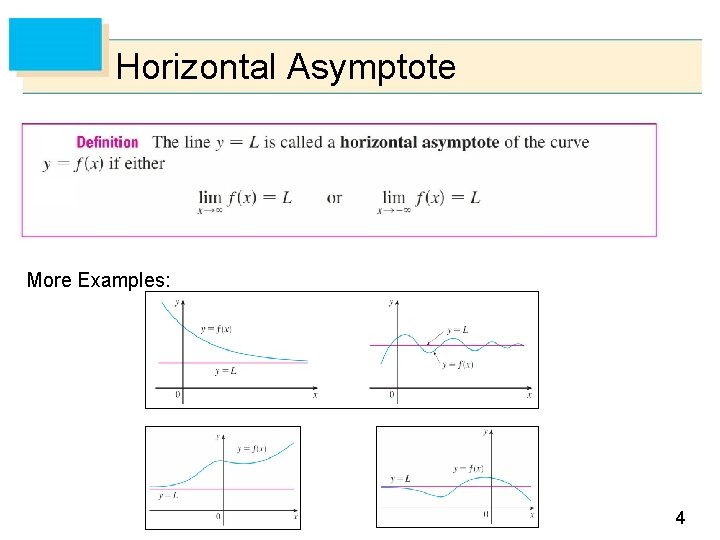
Horizontal Asymptote More Examples: 4

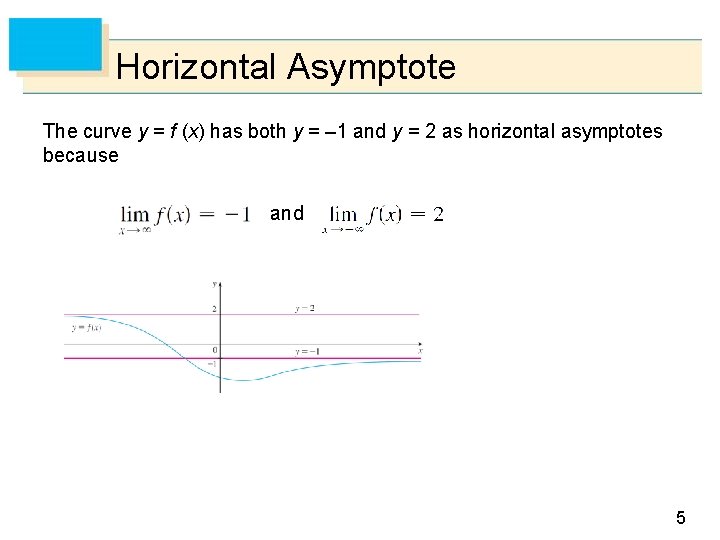
Horizontal Asymptote The curve y = f (x) has both y = – 1 and y = 2 as horizontal asymptotes because and 5

HOW TO EVALUATE A LIMIT AT INFINITY FOR A RATIONAL FUNCTION Step 1: Take the highest power of x in the function’s denominator and divide each term of the fraction by this x power. Step 2: Apply the limit to each term in both numerator and denominator and remember: Step 3: Carefully analyze the results to see if the answer is either a finite number or ∞ or −∞ 6

Reminder: Infinite limits at a number and Vertical Asymptotes This is different from Limits AT infinity! If your direct substitution leads to the form: then the function has a vertical asymptote at x=c. STEPS FOR EVALUATING LIMITS AT VERTICAL ASYMPTOTES Step 1: Make sure the fractional expression in your limit is completely factored. Step 2: Use direct substitution on all the factors which DO NOT BECOME ZERO - make special note of the signs of these numbers you get. Step 3: One of the denominator’s factors will evaluate as 0 so we’ll need to analyze it more carefully. Based on which one-sided limit (left or right approach) you’re evaluating, this factor approaching zero will be positive or negative and VERY SMALL. This VERY SMALL value in the denominator will cause the evaluation of the limit to go infinite. Step 4: Considering all the factors your evaluated in step 2 and the factor approaching 0 you analyzed in step 3: if there an even number of negative factors the limit will evaluate as ‘ ∞ ’ … if there an odd number of negative factors the limit will evaluate as ‘ − ∞ ’. 7

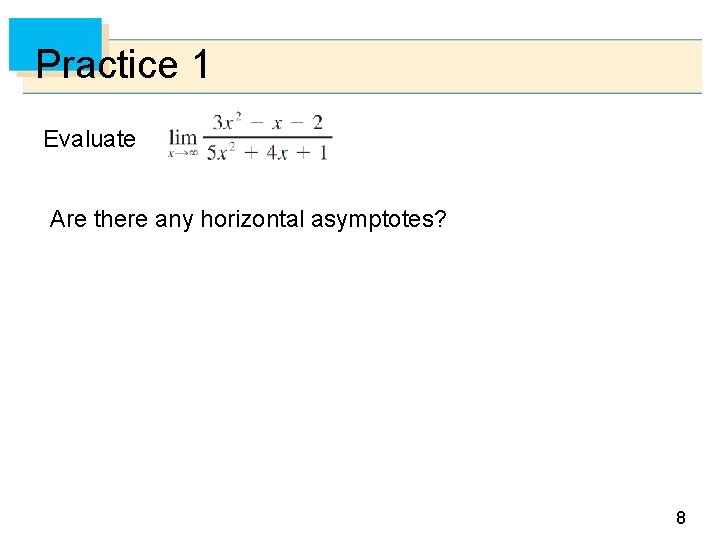
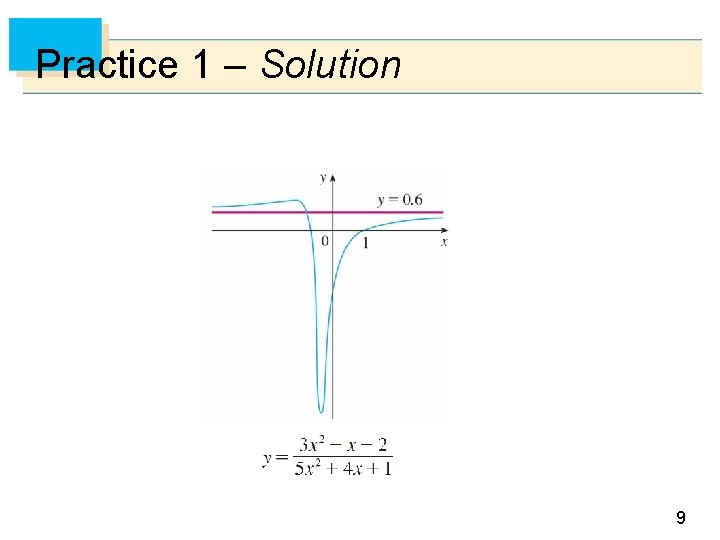
Practice 1 Evaluate Are there any horizontal asymptotes? 8

Practice 1 – Solution 9

Practice 2 Find the horizontal and vertical asymptotes of the graph of the function Solution: Dividing both numerator and denominator by x and using the properties of limits, we have (since = = x for x > 0) 10

Practice 2 – Solution Therefore the line y = graph of f. cont’d is a horizontal asymptote of the 11

Practice 2 – Solution cont’d In computing the limit as x – , we must remember that for x < 0, we have: = |x| =-x So when we divide the numerator by x, for x < 0 we get 12

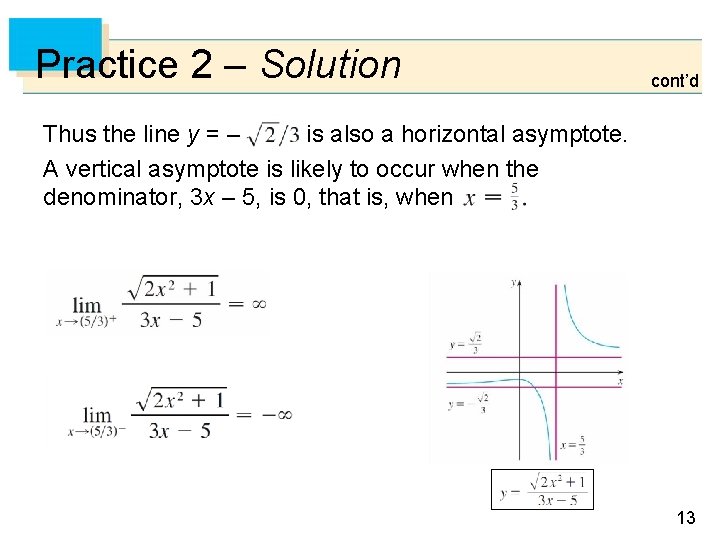
Practice 2 – Solution cont’d Thus the line y = – is also a horizontal asymptote. A vertical asymptote is likely to occur when the denominator, 3 x – 5, is 0, that is, when 13

Infinite Limits at Infinity The notation: is used to indicate that the values of f (x) become large as x becomes large. Similar meanings are attached to the following symbols: 14

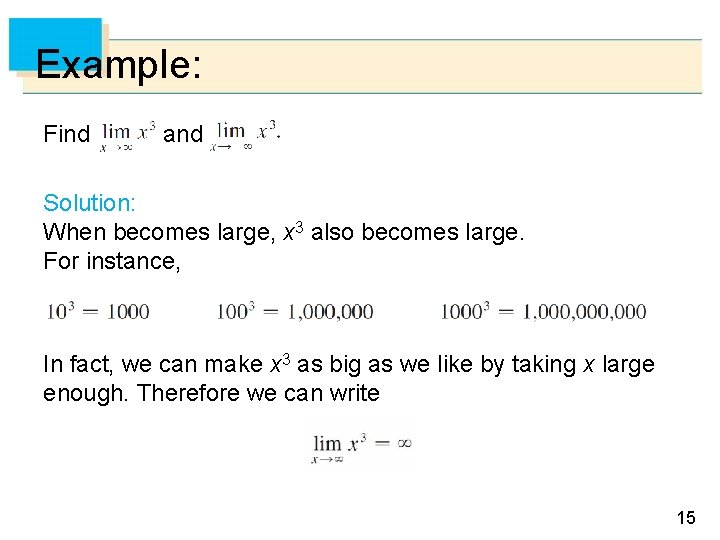
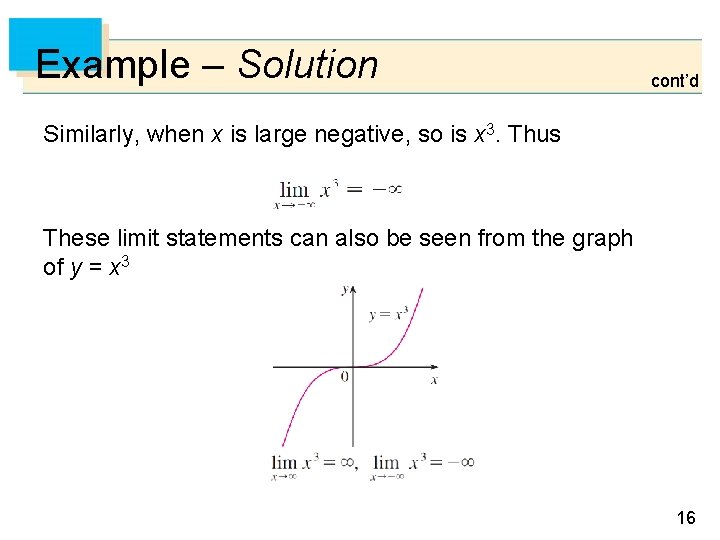
Example: Find and Solution: When becomes large, x 3 also becomes large. For instance, In fact, we can make x 3 as big as we like by taking x large enough. Therefore we can write 15

Example – Solution cont’d Similarly, when x is large negative, so is x 3. Thus These limit statements can also be seen from the graph of y = x 3 16