3 4 Evaluating Logarithms and Graphing Logarithmic Functions

3. 4 Evaluating Logarithms and Graphing Logarithmic Functions Logarithms are important in many applications of mathematics to everyday problems, particularly in biology, engineering, economics and social science. In this section we will show to find a numerical approximation for a logarithm. Because the number system we use is a base 10 system, we will then use logarithms with a base of 10. Logarithms to base 10 are called common logarithms and log 10 x is abbreviated as simply log x, where the base is understood to be 10. Let’s first observe this example with a base of 10. We can solve this by changing from logarithmic form to exponential form to solve. However, this problem could have been solved by another method. Notice in this example, the base is 10. Also, our calculators work with a base of 10. Therefore, we can use our calculator to solve this equation. To evaluate log 10100, find the log button on your calculator. Press the log button then 100 and the equal or enter button. The answer will be 2. On some calculators, you may need to type in the 100 and then press the log button. Next Slide 1

3. 4 Evaluating Logarithms and Graphing Logarithmic Functions Example 1. Evaluate log 1. 98 rounded to four decimal places. Answer: Round to 0. 2967 because the directions are to round to 4 decimal places. We could perform a check to be confident of our answer. Remember the base is understood to be 10. The result is not exactly 1. 98 because we did round off to 4 decimal places. Your Turn Problem #1 Use a calculator to find each common logarithm. Express answer to four decimal places. Answer: 2

3. 4 Evaluating Logarithms and Graphing Logarithmic Functions If the base is not written, then it is assumed to be 10. We can solve this by changing from logarithmic form to exponential form to solve. There are two procedures for evaluating 100. 2956 on your calculator. Type in 10, press the exponent button, then type in 0. 2956. The second method is to use the 10 x key (2 nd then log) on your calculator. Therefore x=1. 9751 rounded to five significant digits. Note: significant digits includes digits in front of the decimal point. Your Turn Problem #2 Use your calculator to find x when given log x. Round to five significant digits. Answer: Note: The two zeros before the four are not significant digits. 3

3. 4 Evaluating Logarithms and Graphing Logarithmic Functions The Natural Logarithm The natural logarithm is a logarithm with a base of e. ‘e’ is approximately 2. 718. You can get this number on your calculator by pressing the ex on your calculator and then using an exponent of 1 to obtain a numerical approximation. You may need to press shift or 2 nd first if the ex key is in small yellow writing above the LN key. The LN key stands for natural logarithm. If an expression is written such as ln 241. 7, the base is assumed to be e. This expression can be found by using the LN key on your calculator. You should get 5. 4877 (rounded to four decimal places) This means e to the power 5. 4877 is approximately 241. 7. Algebraically, we can verify. Since x = 5. 4877, e 5. 4877 241. 7. Example 3. Evaluate ln 225 rounded to four decimal places. Answer: We could perform a check to be confident of our answer. Remember the base is understood to be e. (Instead of using e, you could also use 2. 718 to get an estimate. ) Your Turn Problem #3 Use a calculator to find each natural logarithm. Express answer to four decimal places. Answers: 4

3. 4 Evaluating Logarithms and Graphing Logarithmic Functions The base for ln is assumed to be e. We can solve this by changing from logarithmic form to exponential form to solve. To evaluate e 3. 4 on your calculator, use the ex key on your calculator. Therefore x=29. 964 rounded to five significant digits. Your Turn Problem #4 Use your calculator to find x when given ln x. Round to five significant digits. Answer: 5

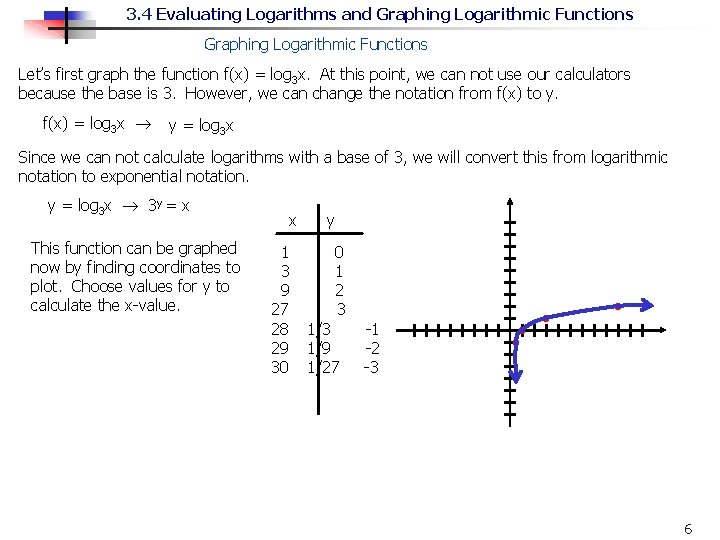
3. 4 Evaluating Logarithms and Graphing Logarithmic Functions Let’s first graph the function f(x) = log 3 x. At this point, we can not use our calculators because the base is 3. However, we can change the notation from f(x) to y. f(x) = log 3 x y = log 3 x Since we can not calculate logarithms with a base of 3, we will convert this from logarithmic notation to exponential notation. y = log 3 x 3 y = x This function can be graphed now by finding coordinates to plot. Choose values for y to calculate the x-value. x 1 3 9 27 28 29 30 y 0 1 2 3 1/9 1/27 -1 -2 -3 6

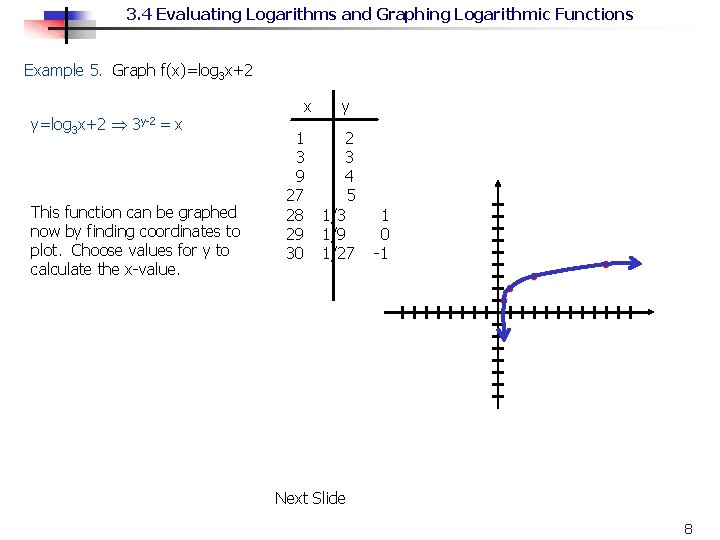
3. 4 Evaluating Logarithms and Graphing Logarithmic Functions In previous sections, we discussed translations of functions. The graph of f(x)=log 3 x+2 is obtained by shifting f(x)=log 3 x up two units. Below are other examples of translations and reflections. 1. 2. 3. 4. f(x)=log 3 x 2 is obtained by shifting f(x)=log 3 x down two units. f(x)=log 3(x 2) is obtained by shifting f(x)=log 3 x two units to the right. f(x)=log 3(x+2) is obtained by shifting f(x)=log 3 x two units to the left. f(x)=-log 3 x is obtained by reflecting f(x)=log 3 x across the through the x axis Graphing a function does not always need to be obtained by translations. Picking points is always a good alternative. For this function, we will first need to change the function from logarithmic form to exponential form. y=log 3 x+2 can be written as y– 2 = log 3 x by subtracting two on both sides. Then converting to logarithmic form, we get 3 y– 2 = x. We can then find points for this by choosing values for y. 7

3. 4 Evaluating Logarithms and Graphing Logarithmic Functions Example 5. Graph f(x)=log 3 x+2 y=log 3 x+2 3 y-2 =x This function can be graphed now by finding coordinates to plot. Choose values for y to calculate the x-value. x 1 3 9 27 28 29 30 y 2 3 4 5 1/3 1/9 1/27 1 0 -1 Next Slide 8

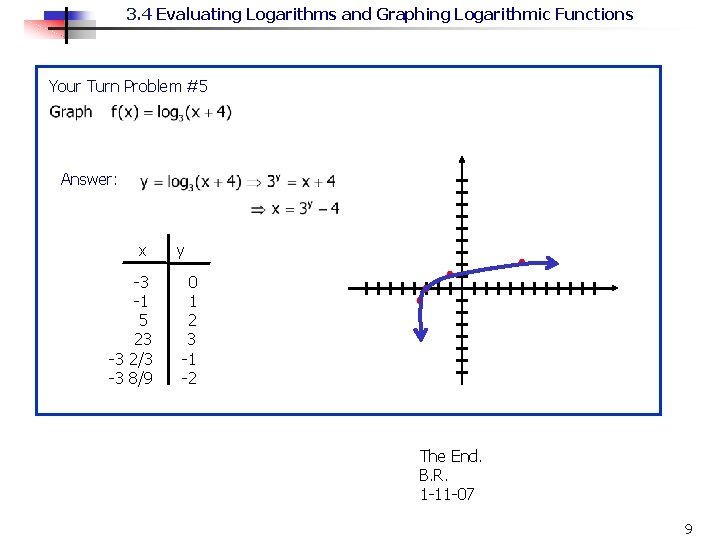
3. 4 Evaluating Logarithms and Graphing Logarithmic Functions Your Turn Problem #5 Answer: x -3 -1 5 23 -3 2/3 -3 8/9 y 0 1 2 3 -1 -2 The End. B. R. 1 -11 -07 9