3 3 Parallel Lines Transversals Postulate 16 Corresponding

  • Slides: 14
Download presentation
3. 3 Parallel Lines & Transversals

3. 3 Parallel Lines & Transversals

Postulate 16 – Corresponding Angles Postulate v If two lines are cut by a

Postulate 16 – Corresponding Angles Postulate v If two lines are cut by a transversal, then the pairs of corresponding s are . 1 2 l m v i. e. If l m, then 1 2.

Section 3. 3 Prove Lines are Parallel Theorems Theorem 3. 4: Alternate Interior Angles

Section 3. 3 Prove Lines are Parallel Theorems Theorem 3. 4: Alternate Interior Angles Converse If alternate interior angles are congruent, then the lines are parallel. Theorem 3. 5: Alternate Exterior Angles Converse If alternate exterior angles are congruent, then the lines are parallel. Theorem 3. 6: Consecutive Int. Angles Converse If consecutive interior angles are supplementary, then the lines are parallel.

EXAMPLE 1 Apply the Corresponding Angles Converse Find the value of x that makes

EXAMPLE 1 Apply the Corresponding Angles Converse Find the value of x that makes m If corr s , then m n. Set angles = to each other. (3 x + 5)o = 65 o 3 x = 60 x = 20 Corr. Angles Converse Subtract 5 Divide by 3

GUIDED PRACTICE for Example 1 1. Is there enough information in the diagram to

GUIDED PRACTICE for Example 1 1. Is there enough information in the diagram to conclude that m n? Explain. 75 o Yes, the supplement to 105 o is 75 o , making corr. angles are congruent , so m n.

EXAMPLE 2 Proving lines parallel Given the information, state the postulate or theorem that

EXAMPLE 2 Proving lines parallel Given the information, state the postulate or theorem that proves lines a and b are parallel? a. 1 5 Alt. Ext. Angles Converse b. 2 5 Corr. Angles Converse c. m 2 m 4 = 180° Consec. Int. Angles Converse d. 3 2 Alt. Int. Angles Converse Is it possible to prove a // b if 1 4? Explain. No, angles would need to be supplementary

GUIDED PRACTICE for Example 2 Can you prove that lines a and b are

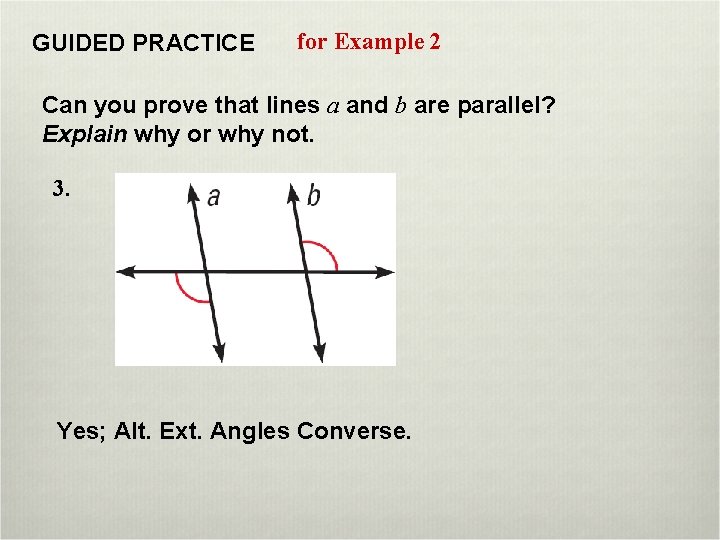
GUIDED PRACTICE for Example 2 Can you prove that lines a and b are parallel? Explain why or why not. 3. Yes; Alt. Ext. Angles Converse.

GUIDED PRACTICE for Example 2 Can you prove that lines a and b are

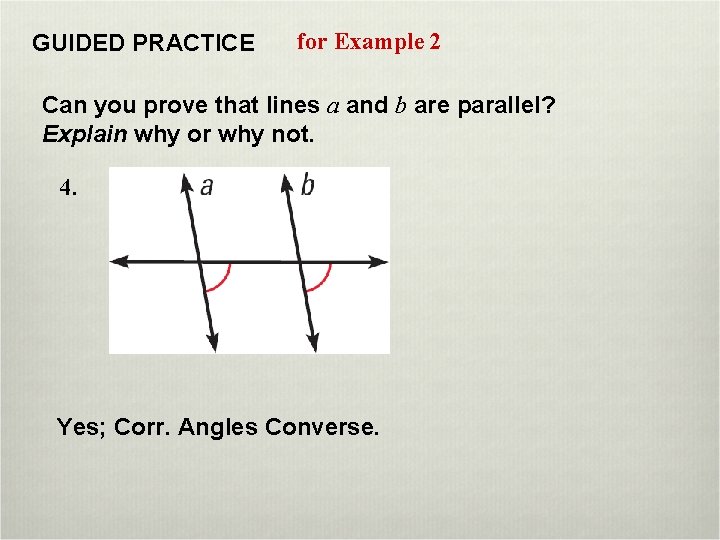
GUIDED PRACTICE for Example 2 Can you prove that lines a and b are parallel? Explain why or why not. 4. Yes; Corr. Angles Converse.

GUIDED PRACTICE for Example 2 Can you prove that lines a and b are

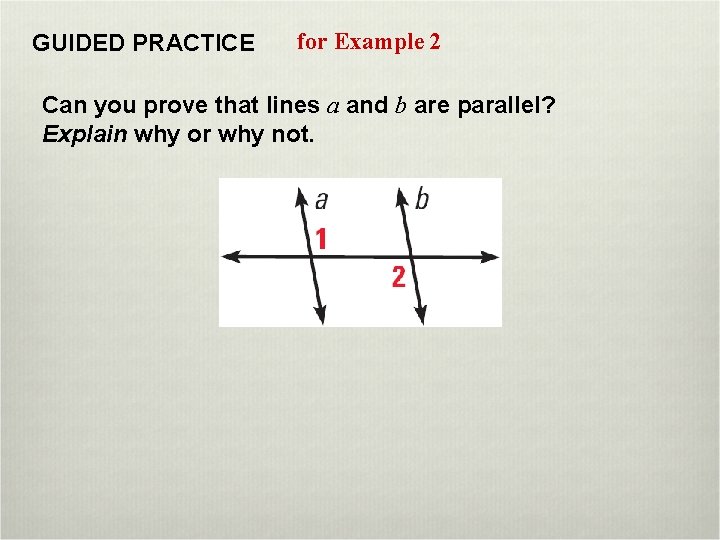
GUIDED PRACTICE for Example 2 Can you prove that lines a and b are parallel? Explain why or why not.

EXAMPLE 3 Prove the Alternate Interior Angles Converse Prove that if alternate interior angles

EXAMPLE 3 Prove the Alternate Interior Angles Converse Prove that if alternate interior angles are congruent, then the lines are parallel. GIVEN : ∠ 4 ∠ 5 PROVE : g // h STATEMENTS REASONS 1. ∠ 4 ∠ 5 1. Given 2. ∠ 1 ∠ 4 2. 3. ∠ 1 ∠ 5 3. Transitive Prop. 4. g // h 4. Vertical ∠s Congruent Corr. Angles Converse

Section 3. 3 Transitive Property of Parallel Lines Theorem 3. 7: Transitive Property of

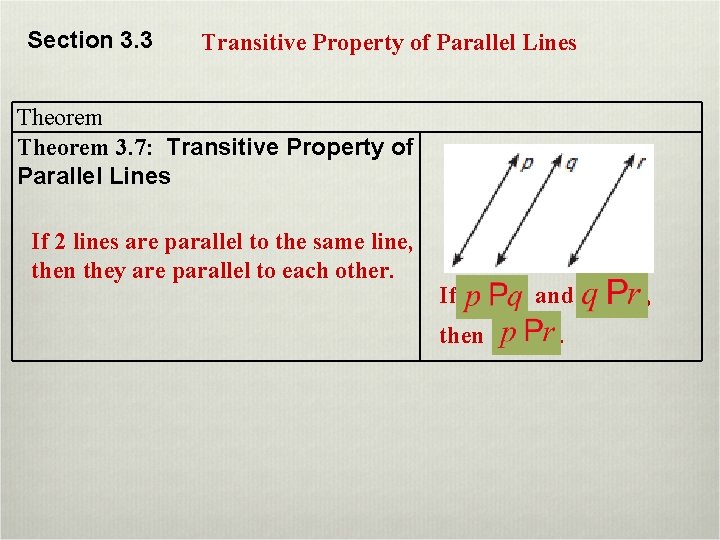
Section 3. 3 Transitive Property of Parallel Lines Theorem 3. 7: Transitive Property of Parallel Lines If 2 lines are parallel to the same line, then they are parallel to each other. If then and. ,

Ex: Find: m 1= m 2= m 3= 1 125 o 2 3 5

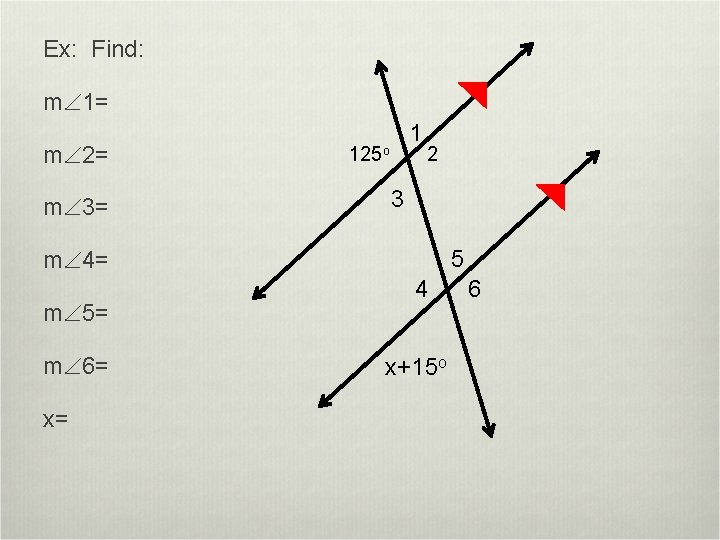
Ex: Find: m 1= m 2= m 3= 1 125 o 2 3 5 m 4= m 5= m 6= x= 4 x+15 o 6

Ex: Find: m 1=55° m 2=125° m 3=55° 1 125 o 3 m 4=125°

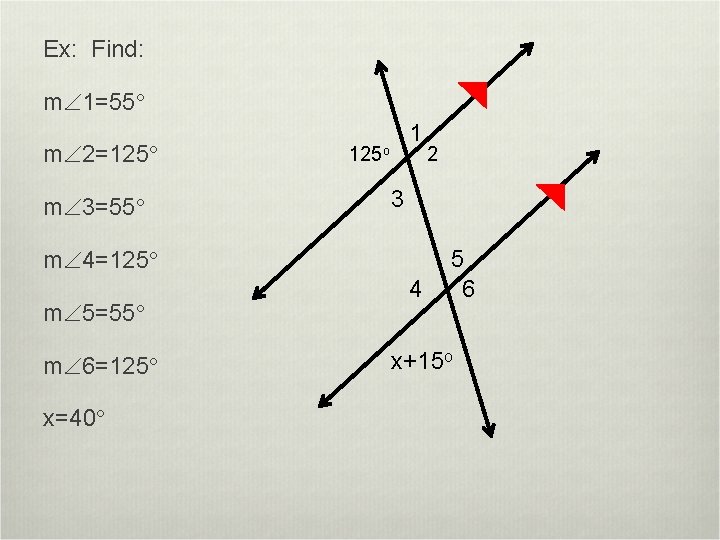
Ex: Find: m 1=55° m 2=125° m 3=55° 1 125 o 3 m 4=125° m 5=55° m 6=125° x=40° 2 4 5 6 x+15 o

Assignment v Handout found on www. kutasoftware. com

Assignment v Handout found on www. kutasoftware. com