3 3 Factored Form of a Quadratic Relation

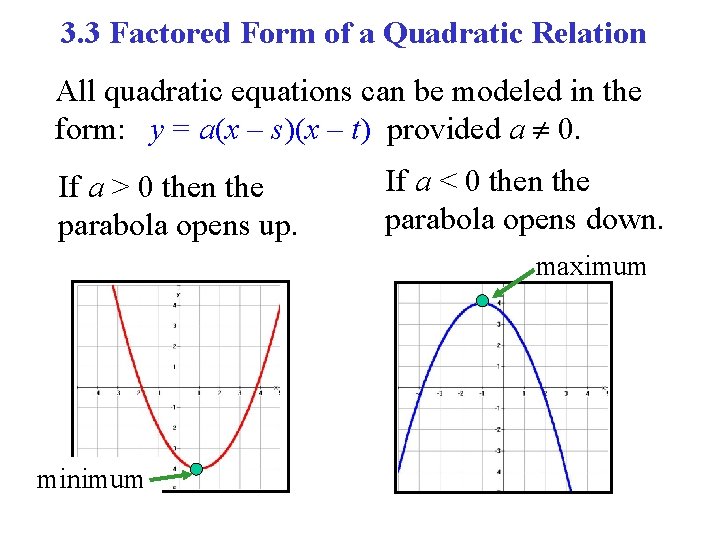
3. 3 Factored Form of a Quadratic Relation All quadratic equations can be modeled in the form: y = a(x – s)(x – t) provided a ¹ 0. If a > 0 then the parabola opens up. If a < 0 then the parabola opens down. maximum minimum

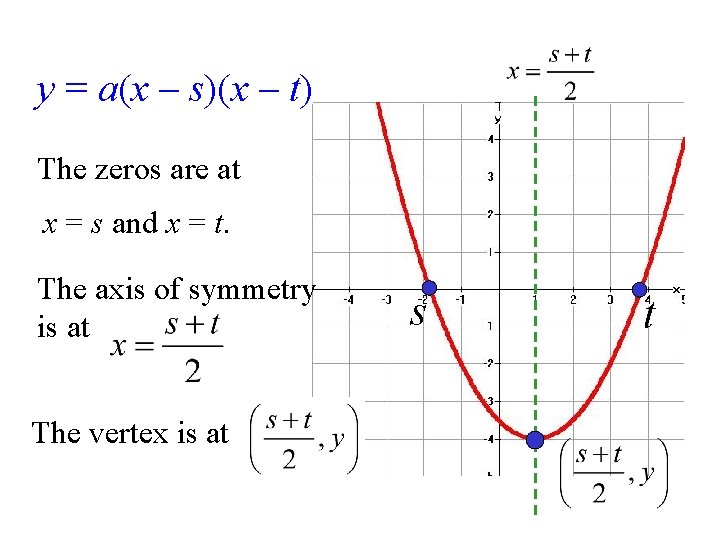
y = a(x – s)(x – t) The zeros are at x = s and x = t. The axis of symmetry is at The vertex is at s t

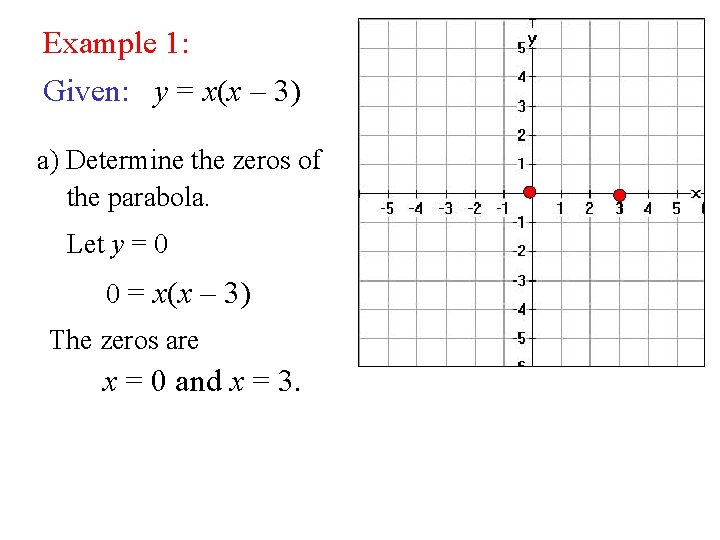
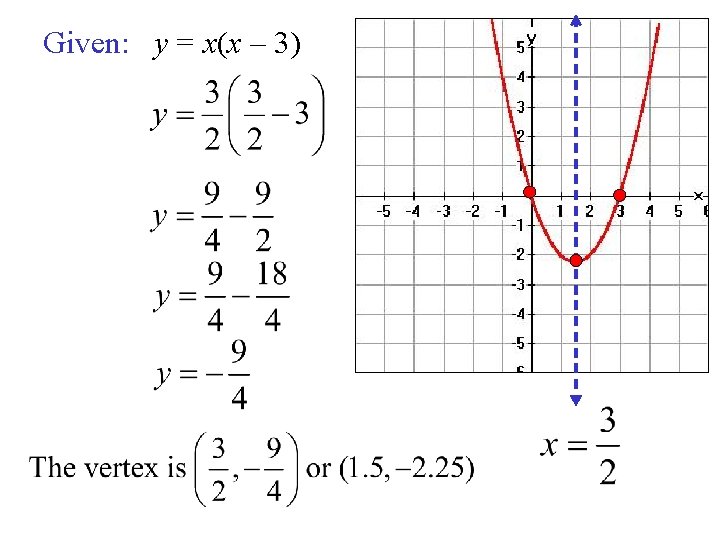
Example 1: Given: y = x(x – 3) a) Determine the zeros of the parabola. Let y = 0 0 = x(x – 3) The zeros are x = 0 and x = 3.

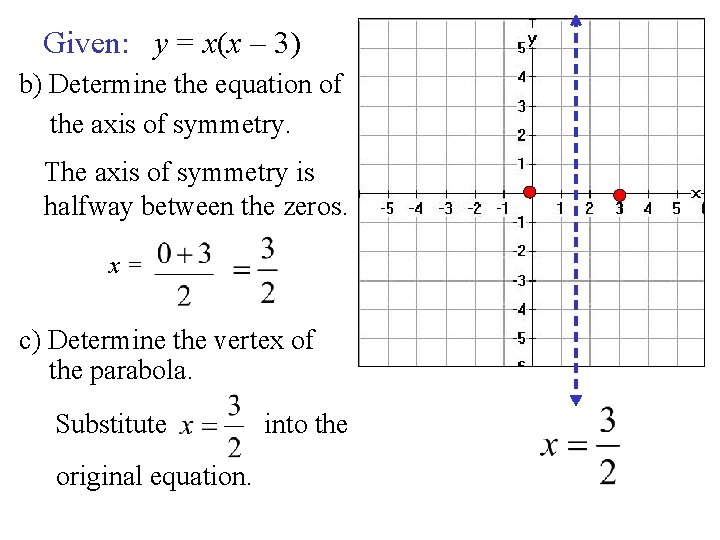
Given: y = x(x – 3) b) Determine the equation of the axis of symmetry. The axis of symmetry is halfway between the zeros. x= c) Determine the vertex of the parabola. Substitute original equation. into the

Given: y = x(x – 3)

Example 2: Determine the zeros and the axis of symmetry of the following: a) A = w(20 – w) w=0 20 – w = 0 20 = w The zeros are at 0 and 20 The axis of symmetry is halfway between 0 and 20. w = 10

Determine the zeros and the axis of symmetry of the following: b) y = 2 x(4 x – 8) 4 x – 8 = 0 4 x = 8 2 x = 0 x=2 The zeros are at 0 and 2 The axis of symmetry is halfway between 0 and 2. x=1

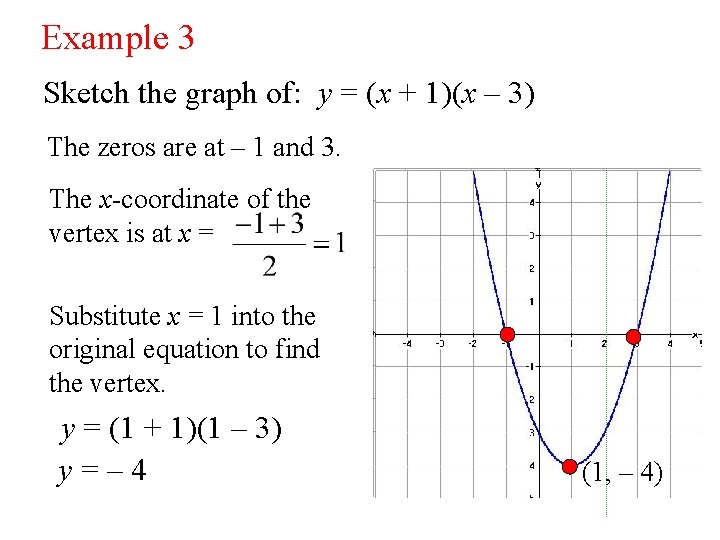
Example 3 Sketch the graph of: y = (x + 1)(x – 3) The zeros are at – 1 and 3. The x-coordinate of the vertex is at x = Substitute x = 1 into the original equation to find the vertex. y = (1 + 1)(1 – 3) y=– 4 (1, – 4)

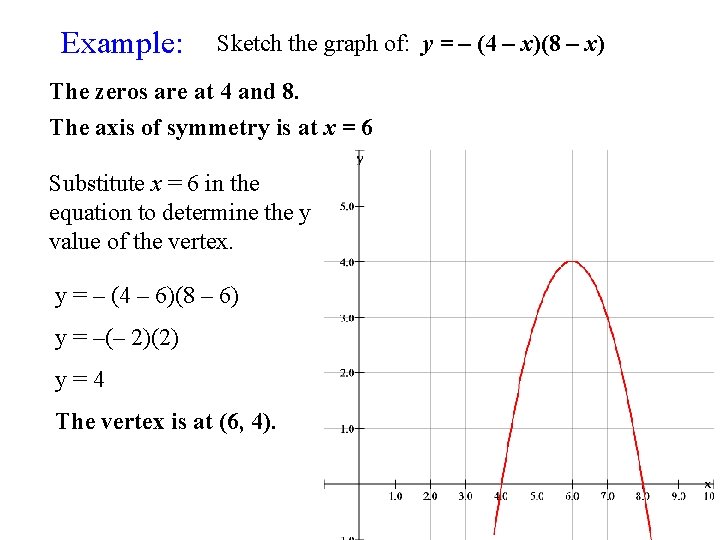
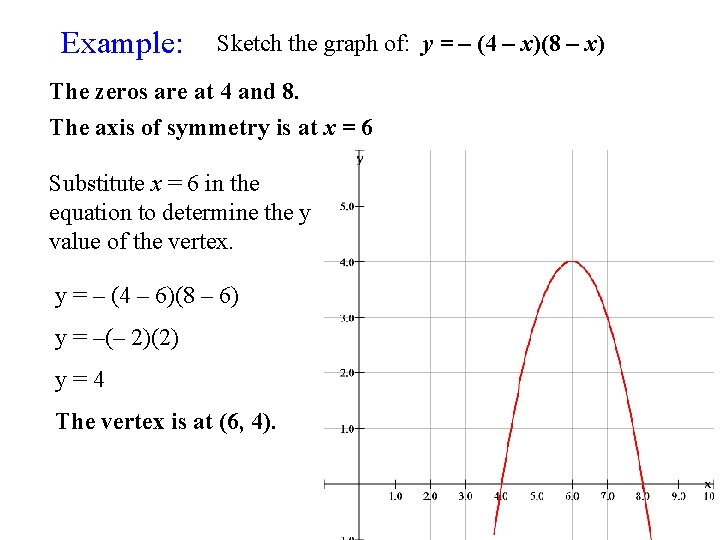
Example: Sketch the graph of: y = – (4 – x)(8 – x) The zeros are at 4 and 8. The axis of symmetry is at x = 6 Substitute x = 6 in the equation to determine the y value of the vertex. y = – (4 – 6)(8 – 6) y = –(– 2)(2) y=4 The vertex is at (6, 4).

Example 4 Determine the equation of the parabola whose xintercepts are 2 and – 3 and whose y-intercept is 6. y = a(x – s)(x – t) sub s = 2 and t = – 3 y = a(x – 2)(x + 3) To find a, substitute (0, 6) into the equation. 6 = a(0 – 2)(0 + 3) 6 = a(– 2)(3) 6 = a(– 6) – 1=a y = – (x – 2)(x + 3)

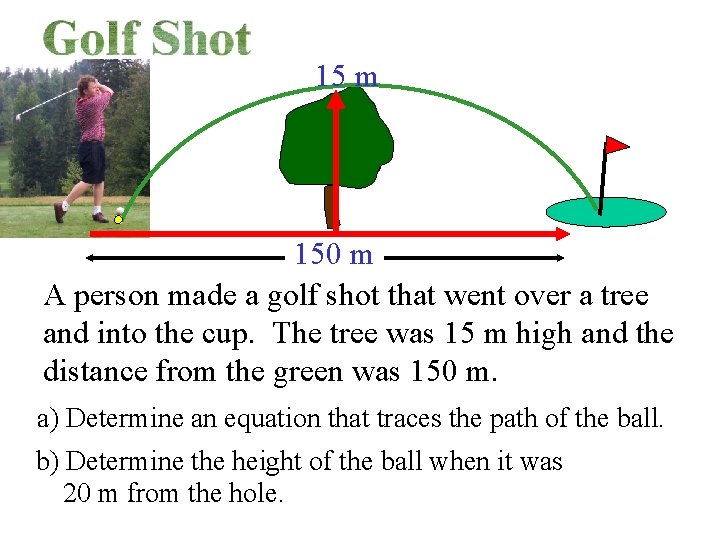
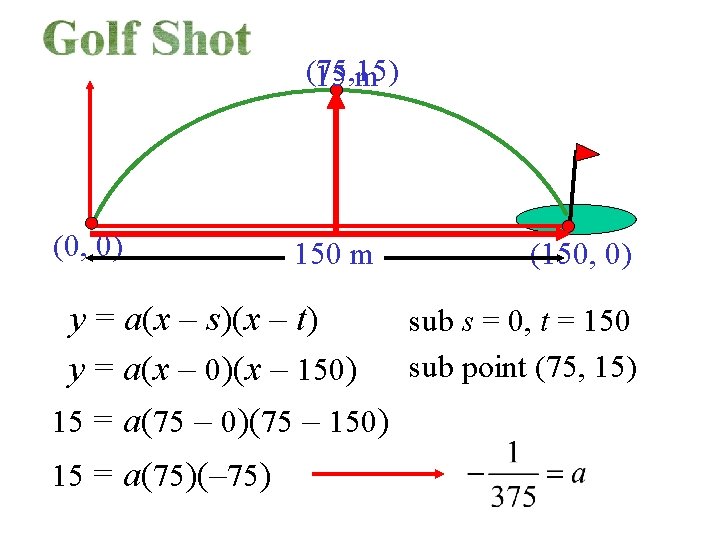
15 m 150 m A person made a golf shot that went over a tree and into the cup. The tree was 15 m high and the distance from the green was 150 m. a) Determine an equation that traces the path of the ball. b) Determine the height of the ball when it was 20 m from the hole.

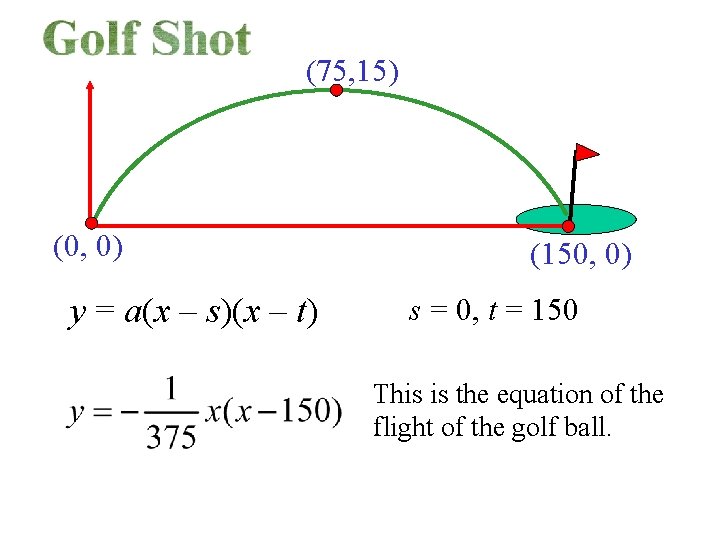
(75, 15) 15 m (0, 0) 150 m (150, 0) y = a(x – s)(x – t) sub s = 0, t = 150 y = a(x – 0)(x – 150) sub point (75, 15) 15 = a(75 – 0)(75 – 150) 15 = a(75)(– 75)

(75, 15) (0, 0) y = a(x – s)(x – t) (150, 0) s = 0, t = 150 This is the equation of the flight of the golf ball.

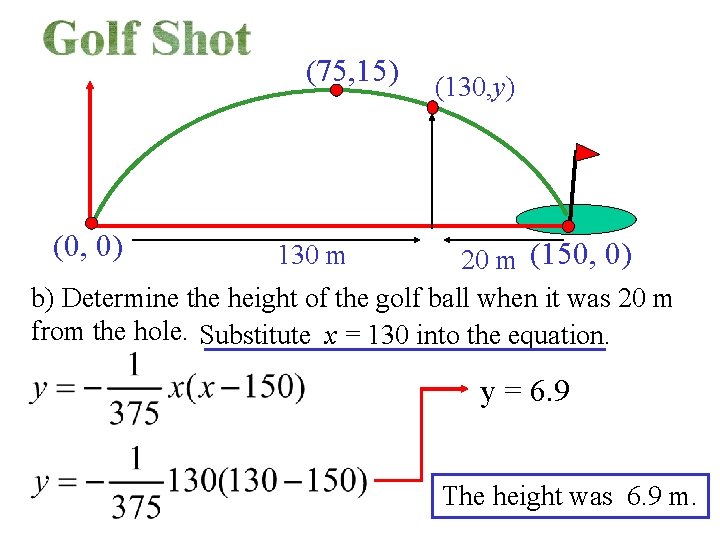
(75, 15) (0, 0) (130, y) 20 m (150, 0) b) Determine the height of the golf ball when it was 20 m from the hole. Substitute x = 130 into the equation. 130 m y = 6. 9 The height was 6. 9 m.

Retailing Problem: Maximizing CD Revenue. Max operates a store that sells CDs. All CDs sell for $20 each. In order to increase revenue, he decides to increase his price. He knows that over the last six months he has sold an average of 280 Cd’s per day at $20 each. Market research indicates that for every $0. 50 increase in price, daily sales will drop by five units. What unit price will maximize Max’s daily profit?

Let x represent the number of price increases. Let 5 x represent each loss of sales. Recall: Revenue = Price × number of units sold Price = 20 + 0. 50 x Number of CDs sold = 280 – 5 x

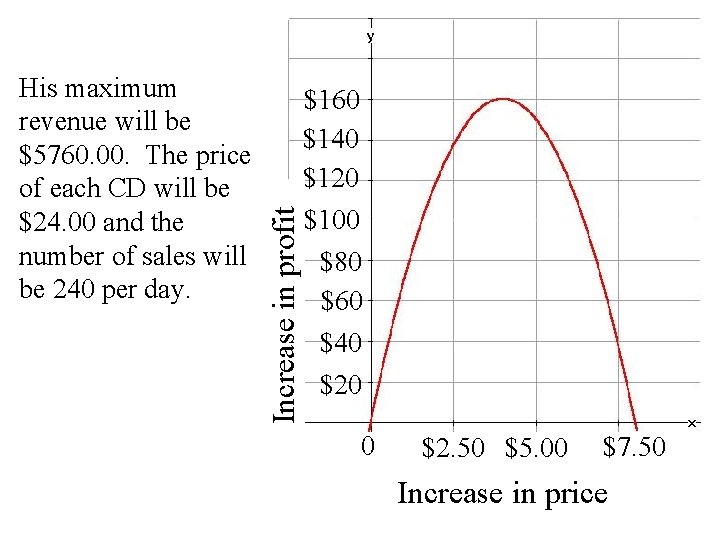
Equation: Revenue = price × number of CDs sold Revenue = (20 + 0. 50 x)(280 – 5 x) Determine the zeros: 20 + 0. 50 x = 0 280 – 5 x = 0 20 = – 0. 50 x 280 = 5 x – 40 = x 56 = x The zeros are at – 40 and 56 The axis of symmetry is at: =8 Substitute x = 8 into the equation. Revenue = (20 + 0. 50× 8)(280 – 5× 8) = (24. 00)(240) = $5760. 00 is the maximum revenue

Increase in profit His maximum revenue will be $5760. 00. The price of each CD will be $24. 00 and the number of sales will be 240 per day. $160 $140 $120 $100 $80 $60 $40 $20 0 $2. 50 $5. 00 $7. 50 Increase in price

Example: Sketch the graph of: y = – (4 – x)(8 – x) The zeros are at 4 and 8. The axis of symmetry is at x = 6 Substitute x = 6 in the equation to determine the y value of the vertex. y = – (4 – 6)(8 – 6) y = –(– 2)(2) y=4 The vertex is at (6, 4).

Example The x-intercepts are – 1 and – 3 and the y-intercept is – 3. Determine the equation of the parabola. y = a(x + 1)(x + 3) sub (0, – 3) into the equation – 3 = a(0 + 3)(0 + 1) – 3 = 3 a – 1 = a equation y = – (x + 1)(x + 3)

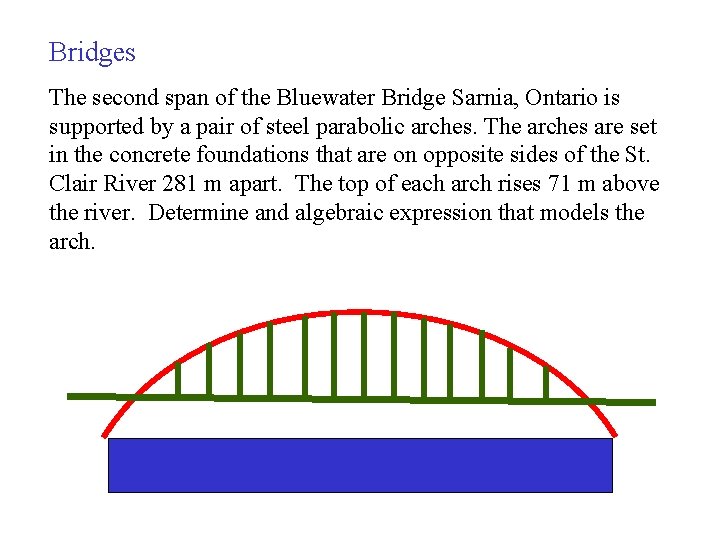
Bridges The second span of the Bluewater Bridge Sarnia, Ontario is supported by a pair of steel parabolic arches. The arches are set in the concrete foundations that are on opposite sides of the St. Clair River 281 m apart. The top of each arch rises 71 m above the river. Determine and algebraic expression that models the arch.

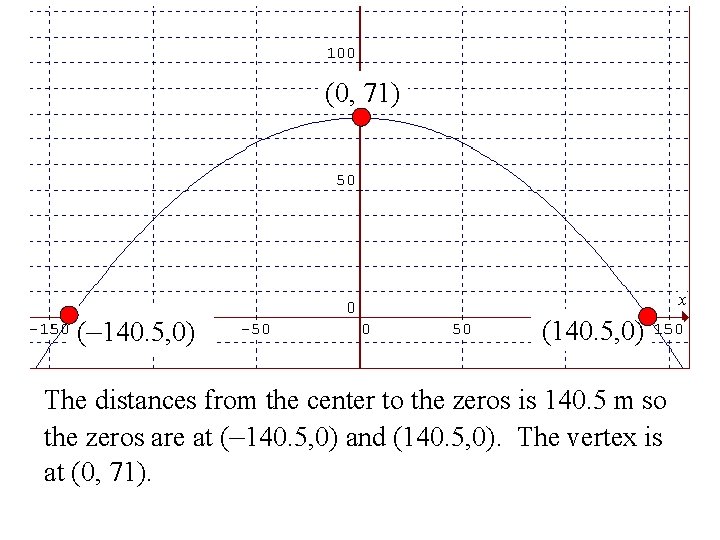
(0, 71) (– 140. 5, 0) (140. 5, 0) The distances from the center to the zeros is 140. 5 m so the zeros are at (– 140. 5, 0) and (140. 5, 0). The vertex is at (0, 71).

y = a(x – s)(x – t) s = – 140. 5 and t = 140. 5 y = a( x + 140. 5)(x – 140. 5) To solve for a, substitute (0, 71) 71 = a(0 + 140. 5)(0 – 140. 5) 71 = a(– 140. 5)(140. 5) 71 = a(– 19740. 25) – 0. 004 = a Equation: y = – 0. 004(x – 140. 5)(x + 140. 5)