3 2 Solving Linear Systems Algebraically ObjectivesAssignment Use

3. 2 Solving Linear Systems Algebraically

Objectives/Assignment • Use algebraic methods to solve linear systems. • Assignment 11 -53 odd

Warm-Up y = 2 x-5 x = 3 – 2 y y = (3/4)x -3 x = 4 – (4/3)y

The Substitution Method Solve this equation for x Substitute -2 y + 2 for x in the first equation. 3 x + 4 y = -4 3(-2 y+2)+4 y = -4 Finally, substitute 5 for y (in x = -2 y +2) and solve for x. x = -2 y + 2 -6 y+6+4 y = -4 x = -8 y=5 (-8, 5) is the solution to the system.

The Substitution Method Check the ordered pair (-8, 5) by substituting it into each equation to verify it is really the solution. x = -8 y=5 (-8, 5) is the solution to the system.

The Linear Combination Method: Multiplying One Equation Multiply the first equation by -2 -2 Add the equations together Use this value for y and substitute it into either of the equations. Solve for x. 4 x – 5(-6) = 8 3 y = -18 y = -6 The ordered pair (-11/2, -6) is the solution to this system x=-(11/2)

The Linear Combination Method: Multiplying One Equation Multiply the first equation by -2 -2 3 y = -18 Why Choose the multiplier -2? ? y = -6 The ordered pair (-11/2, -6) is the solution to this system x=-(11/2)

(1/2, 4)

Solve the system using the Linear Combination Method. (-1, 5)

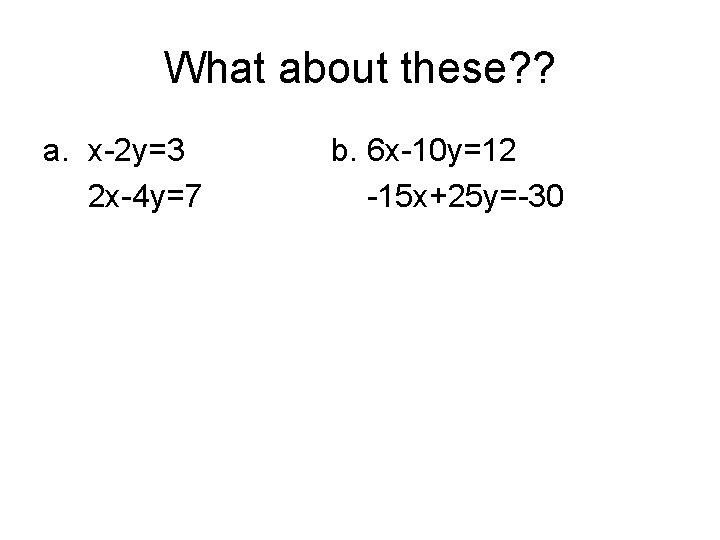
What about these? ? a. x-2 y=3 2 x-4 y=7 b. 6 x-10 y=12 -15 x+25 y=-30