3 2 Solving by Substitution or Elimination n

3. 2 Solving by Substitution or Elimination n The Substitution Method n The Elimination Method n Comparing Methods Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

The Substitution Method Algebraic (nongraphical) methods for solving systems are often superior to graphing, especially when fractions are involved. One algebraic method, the substitution method, relies on having a variable isolated. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 2

Example (substitution method) Solve the system (1) The equations (2) are numbered for reference. Solution Equation (2) says that y and x – 1 name the same number. Thus we can substitute x – 1 for y in equation (1): x+y=2 Equation (1) x + (x – 1) = 2 Substituting x – 1 for y We solve the last equation: Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 3

Solution (continued) x + (x – 1) = 2 2 x – 1 = 2 2 x = 3 Now return to the original pair of equations and substitute 3/2 for x in either equation so that we can solve for y x= . Equation (2) y = 3/2 – 1 y= Substituting 3/2 for x . Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 4

Solution (continued) We obtain the ordered pair We can plug the ordered pair into the original pair of equations to check that it is the solution. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 5

Example (substitution method) Solve the system (1) (2) Solution First, select an equation to solve for one variable. To isolate y, subtract 3 x from both sides of equation (1): (1) (3) Next, proceed as in the last example, by substituting: Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 6

Solution (continued) 2 x – 3 y = 7 2 x – 3(5 – 3 x) = 7 2 x – 15 + 9 x = 7 11 x = 22 x = 2. Equation (2) Substituting 5 – 3 x for y We can substitute 2 for x in either equation (1), (2), or (3). It is easiest to use (3) because it has already been solved for y: y = 5 – 3(2) y = – 1. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 7

Solution (continued) We obtain the ordered pair (2, – 1). We can plug the ordered pair into the original pair of equations to check that it is the solution. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 8

Example (substitution method) Solve the system (1) (2) Solution We can substitute 7 y + 2 for x in equation (1) and solve: 7 y + 2 = 7 y + 5 Substituting 7 y + 2 for x 2 = 5. Subtracting 7 y from both sides When the y terms drop out, the result is a contradiction. We state that the system has no solution. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 9

The Elimination Method The elimination method for solving systems of equations makes use of the addition principle: If a = b, then a + c = b + c. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 10

Example (elimination method) (1) Solve the system (2) Solution Note that according to equation (2), –x + y and 9 are the same number. Thus we can work vertically and add –x + y to the left side of equation (1) and 9 to the right side: x + y = 5 (1) –x + y = 9 0 x + 2 y = 14. (2) Adding Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 11

Solution (continued) This eliminates the variable x, and leaves an equation with just one variable, y for which we solve: 2 y = 14 y=7 Next, we substitute 7 for y in equation (1) and solve for x: x+7=5 Substituting. We also could have used equation (2). x = – 2 Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 12

Solution (continued) We obtain the ordered pair (– 2, 7). We can plug the ordered pair into the original pair of equations to check that it is the solution. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 13

Example (elimination method) Solve the system (1) (2) Solution To clear the fractions in equation (2), we multiply both sides of equation (2) by 12 to get equation (3): (3) Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 14

Solution (continued) Now we solve the system (1) (3) Notice that if we add equations (1) and (3), we will not eliminate any variables. If the – 2 y in equation (1) were changed to – 4 y, we would. To accomplish this change, we multiply both sides of equation (1) by 2: 2 x – 4 y = – 12 Multiply eqn. (1) by 2 3 x + 4 y = 12 (3) Adding 5 x + 0 y = 0 Solving for x x = 0. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 15

Solution (continued) Then 3(0) + 4 y = 12 y=3 Substituting 0 for x in equation (3) We obtain the ordered pair (0, 3). We can plug the ordered pair into the original pair of equations to check that it is the solution. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 16

Example (elimination method) Solve the system (1) (2) Solution 4 x – 6 y = 4 – 4 x + 6 y = – 4 0=0 Multiply equation (1) by 2 Add Note that what remains is an identity. Any pair that is a solution of equation (1) is also a solution of equation (2). The equations are dependent and the solution set is infinite: Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 17

Rules for Special Cases When solving a system of two linear equations in two variables: 1. If an identity is obtained, such as 0 = 0, then the system has an infinite number of solutions. The equations are dependent and, since a solution exists, the system is consistent. 2. If a contradiction is obtained, such as 0 = 7, then the system has no solution. The system is inconsistent. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 18

Comparing the Methods Method Strengths Graphical Solutions are displayed graphically. Can be used with any system that can be graphed. Weaknesses Inexact when solutions involve numbers that are not integers. Solution may not appear on the part of the graph drawn. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 19

Comparing the Methods Method Strengths Substitution Yields exact solutions. Easy to use when a variable is alone on one side. Weaknesses Introduces extensive computations with fractions when solving more complicated systems. Solutions are not displayed graphically. Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 20

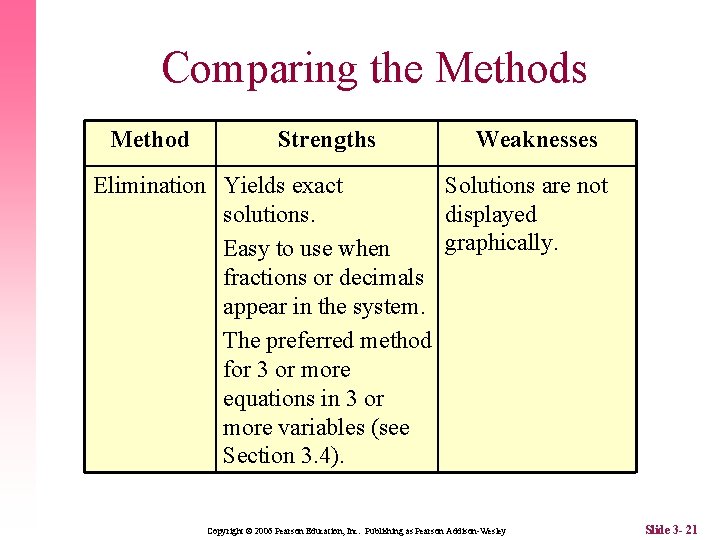
Comparing the Methods Method Strengths Weaknesses Elimination Yields exact Solutions are not solutions. displayed graphically. Easy to use when fractions or decimals appear in the system. The preferred method for 3 or more equations in 3 or more variables (see Section 3. 4). Copyright © 2006 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3 - 21