3 2 Ensimmisen asteen polynomifunktio E 2 Laske

3. 2. Ensimmäisen asteen polynomifunktio E. 2. Laske funktion f(x) = 4 x - 3 arvo, kun x = 2 f(2) = 4 · 2 - 3 = 5

3. 2. 2 Funktion määrittelyjoukko (MJ) Ne muuttujan arvot, joilla funktion arvot voidaan laskea E. 4. Mikä on funktion määrittelyjoukko, kun a) f(x) = x + 1 b) a) R b) x ≥ 0 c) x ≠ 1 c)

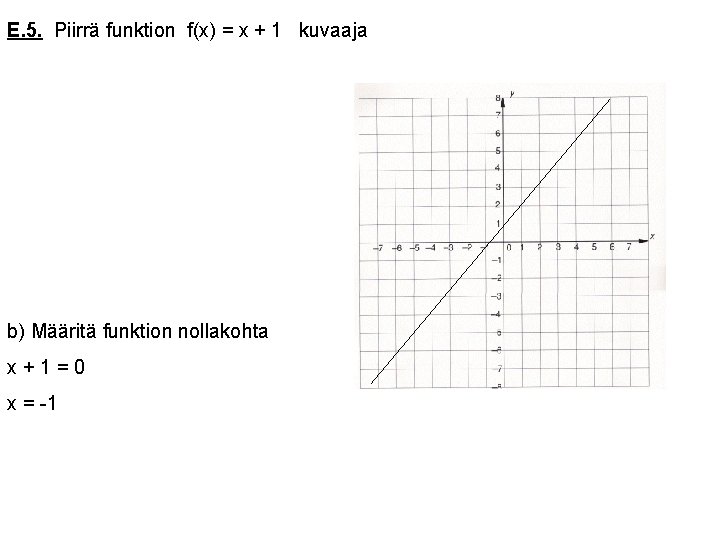
E. 5. Piirrä funktion f(x) = x + 1 kuvaaja b) Määritä funktion nollakohta x+1=0 x = -1

Lineaarinen funktio y = kx + b Kuvaaja on suora k = kulmakerroin jos k > 0, niin suora on nouseva jos k < 0, niin suora on laskeva jos k = 0, niin suora on x-akselin suuntainen ilmoittaa myös jyrkkyyden b = vakiotermi suoran ja y-akselin leikkauspisteen y-koordinaatti

E. 7. Suorien yhtälöt ovat 6 x + 2 y = 2 ja 2 x + 4 y - 4 = 0. a) Määritä suorien kulmakertoimet b) Ovatko suorat nousevia vai laskevia c) Kumpi suora on jyrkempi a) 2 y = -6 x + 2 4 y = -2 x + 4 y = -3 x + 1 y = -½ x + 1 k = -3 k = -½ b) laskevia, koska k < 0 c) y = -3 x + 1 on jyrkempi

Kirjan esimerkki 3, s. 75 Määritä pisteiden (-1, 1) ja (2, 0) kautta kulkevan suoran yhtälö. Suoran yhtälö muotoa y = kx + b Suoralla olevat pisteet toteuttavat yhtälön: 1 = -k + b 0 = 2 k + b 3 k = -1/3 sijoitus: 2*(-1/3) + b = 0 b = 2/3

E. 1. Ratkaise yhtälöpari | 3 y sijoittamalla: | (-2) 4·½ + 2 y = 7 – 2 2 y = 5 2 x = 1 y = 2½ x=½ V: x = ½, y =2½ Tarkistus: 4 ½ + 2 2½ = 7 . /. 5 ½ + 3 2½ = 10. /.

E. 2. Ratkaise yhtälöpari T 1 5 x = -5 x = -1 y sijoittamalla: y = 2 (-1) = – 2 V: x = -1, y = -2

T. 2. Ratkaistaan ensin y: 2 x – y = 0 y = 2 x Sijotetaan alempaa yhtälöön: 3 x + 2 x + 5 = 0 5 x = – 5 x = -1 y sijoittamalla: y = 2 (-1) = – 2 V: x = -1, y = -2

T. 3. Ratkaistaan ensin molemmista y: 2 x – y = 0 y = 2 x 3 x + y + 5 = 0 y = -3 x – 5 Merkitään y: n lausekkeet yhtä suuriksi: 2 x = -3 x – 5 2 x + 3 x = -5 5 x = -5 x = -1 y sijoittamalla: y = 2 (-1) = – 2 V: x = -1, y = -2

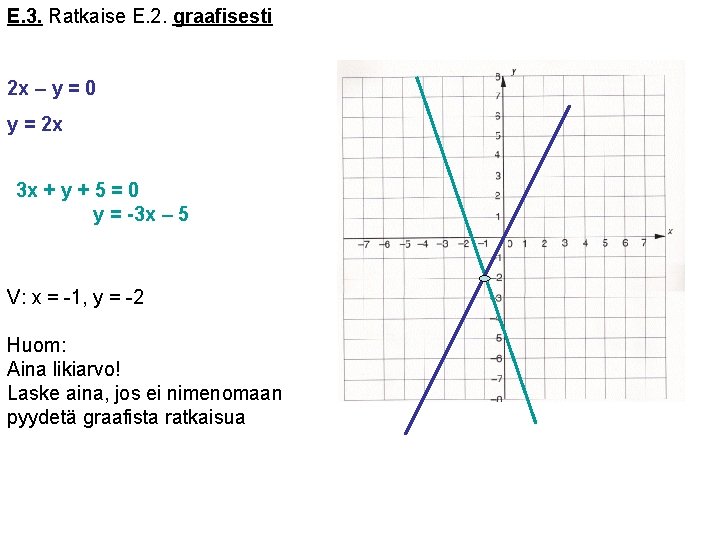
E. 3. Ratkaise E. 2. graafisesti 2 x – y = 0 y = 2 x 3 x + y + 5 = 0 y = -3 x – 5 V: x = -1, y = -2 Huom: Aina likiarvo! Laske aina, jos ei nimenomaan pyydetä graafista ratkaisua

E. 5. Ratkaise yhtälöpari | (-2) | 1 -21 = 0 epätosi V: Yhtälöllä ei ole ratkaisua

E. 6. Ratkaise yhtälöpari 0 =0 tosi V: Kaikki suoran x – 2 y + 1 = 0 pisteet

Yhtälöparin sovelluksia E. 1. Kuinka monta kanaa ja kania on miehen säkissä, kun päitä on yhteensä 8 ja jalkoja 22? x = kanojen lkm Sijoittamalla: y = kanien lkm *) x+3=8 x=8– 3 * | (-2) | 1 x=5 V: 5 kanaa ja 3 kania 2 y = 6 y=3 | : 2

Reaalilukuvälit E. 2. Esitä epäyhtälöin väli a) 1, 4 b) ]0, 3] c) [-2, [ a) 1 ≤ x ≤ 4 b) 0 < x ≤ 3 c) x ≥ -2 E. 3. Esitä hakasuluin väli a) 6 < x < 8 b) 4 x < 10 a) ]6, 8[ b) [4, 10[ c) ]- ∞, 4[ c) x < 4

EPÄYHTÄLÖN RATKAISEMINEN E. 4. Ratkaise epäyhtälö a) 3 x + 2 < x + 8 3 x – x < 8 – 2 2 x < 6 x<3 b) 2 x – 3 < 4 x + 5 2 x – 4 x < 5 + 3 -2 x < 8 x > -4 b) 2 x – 3 < 4 x + 5

E. 5. a) b) | *4 2 x < 2 x + 1 2 x -2 x < 1 0<1 tosi x R x(x – 4) < (x – 5)(x+1) x 2 – 4 x < x 2 + x – 5 x 2 – 4 x – x 2 – x + 5 x < -5 0 < -5 epätosi V: ei ratkaisua

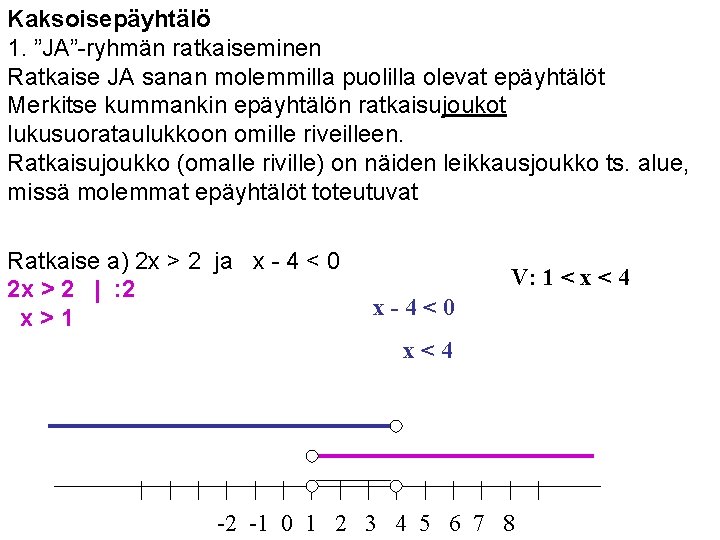
Kaksoisepäyhtälö 1. ”JA”-ryhmän ratkaiseminen Ratkaise JA sanan molemmilla puolilla olevat epäyhtälöt Merkitse kummankin epäyhtälön ratkaisujoukot lukusuorataulukkoon omille riveilleen. Ratkaisujoukko (omalle riville) on näiden leikkausjoukko ts. alue, missä molemmat epäyhtälöt toteutuvat Ratkaise a) 2 x > 2 ja x - 4 < 0 2 x > 2 | : 2 x>1 V: 1 < x < 4 x-4<0 x<4 -2 -1 0 1 2 3 4 5 6 7 8

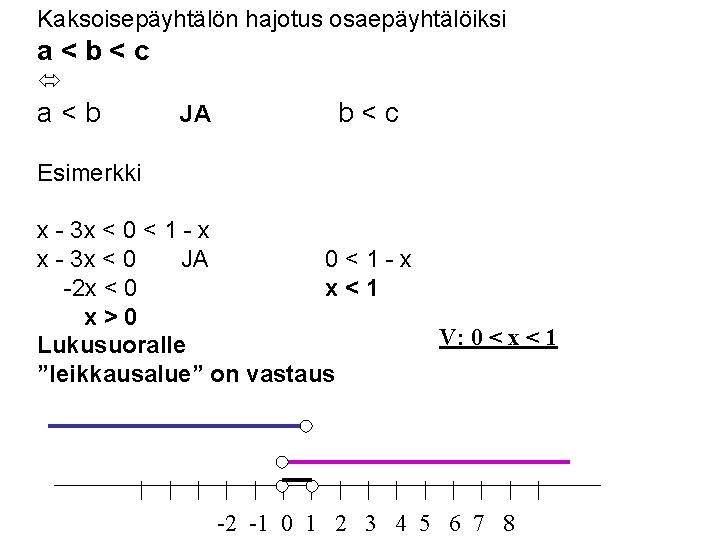
Kaksoisepäyhtälön hajotus osaepäyhtälöiksi a<b<c a<b JA b<c Esimerkki x - 3 x < 0 < 1 - x x - 3 x < 0 JA 0<1 -x -2 x < 0 x<1 x>0 Lukusuoralle ”leikkausalue” on vastaus V: 0 < x < 1 -2 -1 0 1 2 3 4 5 6 7 8

Eksponenttifunktio y = kx Kuvaaja on koko ajan x-akselin yläpuolella, kulkee pisteen (0, 1) kautta (k > 0) Määrittelyjoukko on koko R Arvojoukko on R+ eli positiivisten reaalilukujen joukko kx on kasvava, jos k > 1 ELI kantaluku on > 1 kx on vähenevä, jos 0 < k < 1 eli kantaluku välillä ]0, 1[ kx on vakiofunktio, jos k = 1

Eksponenttiyhtälöitä Yhtälö, jossa kaksi termiä ja sama kantaluku Siirrä termit eri puolelle yhtälöä kx = ky x = y Esimerkki 3 x = 9 3 x = 3 2 x=2 7 x-3 = 49 x 7 x-3 = (72)x 7 x-3 = 72 x x - 3 = 2 x x = -3

Eksponenttiepäyhtälöitä Epäyhtälö, jossa kaksi termiä ja sama ykköstä suurempi kantaluku Siirrä termit eri puolille epäyhtälöä. kx < ky x < y (kun k > 1) Epäyhtälö, jossa kaksi termiä ja sama ykköstä pienempi kantaluku Muuten samoin kuin yllä, mutta Käytä sääntöä kx < ky x > y (kun 0 < k < 1) Esimerkki 4 x-1 < 8 3 x > 81 (22)x -1 < 23 3 x > 3 4 22(x - 1) < 23 x>4 2(x - 1) < 3 2 x - 2 < 3 2 x < 5 x < 2, 5

Esimerkki Bakteerikanta kolminkertaistuu tunnissa Jos kannan suuruus nyt on 25 miljardia Kuinka paljon bakteereja on a) Neljän tunnin kuluttua b) Neljä tuntia sitten c) Puoli tuntia sitten a) 34 * 25 = 2000 (miljardia) b) 3 -4 * 25 = 0, 31 (miljardia) c) 3 -0, 5 * 25 = 14 (miljardia)

Esimerkki Radioaktiivisen aineen määrä pienenee kahdeksassa päivässä neljännekseen alkuperäisestä. Kuinka monta prosenttia aineesta hajoaa vuorokaudessa? a = alkuperäinen määrä k 8 * a = 0, 25 a k 8 = 0, 25 Vuorokaudessa aineen määrä tulee 0, 84 -kertaiseksi eli aineesta hajoaa 16%

POLYNOMIT E. 1. Mitkä ovat polynomin P(x) = 5 x 3 – 2 x + a a) termit b) termien kertoimet c) asteluku d) Onko polynomi monomi, binomi vai trinomi? a) 5 x 3, -2 x ja a (vakiotermi) b) 5, -2, a c) 3 d) trinomi

E. 2. Polynomin 2 x + 1 aste on 1 kuvaaja on suora E. 3. Polynomin x 2 – 1 aste on 2 kuvaaja on paraabeli

POLYNOMIN ARVON LASKEMINEN Sijoitetaan muuttujan paikalle se luku, jolla polynomin arvoa ollaan laskemassa E. 4. Laske P(1), P(-2) kun a) P(x) = x 2 – 2 b) P(x) = -x 2 + 2 x + a a) P(1) = 12 – 2 = -1 P(-2) = (-2)2 – 2 = 4 – 2 = 2 b) P(1) = -12 + 2· 1 + a = -1 + 2 + a = 1 + a P(-2) = -(-2)2 + 2 · (-2) + a = -4 – 4 + a = -8 + a

E. 5. a) Millä x: n arvolla P(x) = 2 x – 4 saa arvon 6 b) Ratkaise yhtälö P(x) = 0, kun P(x) = 2 x + 1 a) P(x) = 6: 2 x – 4 = 6 2 x = 10 x=5 b) P(x) = 0 2 x + 1 = 0 2 x = -1 x = -½

POLYNOMIN YHTEEN- JA VÄHENNYSLASKU E. 7. Laske a) 4 x 3 + 3 x 3 = 7 x 3 b) 7 x 3 + 3 x 2 – 2 x 2 = 7 x 3 + x 2 c) 4 x 3 – 2 x 2 + 1 + 4 x 2 – 3 x 3 – 2 = x 3 + 2 x 2 - 1

E. 8. Määritä polynomin P(x) = -x 2 – 5 x + 2 vastapolynomi -P(x) = -(-x 2 – 5 x + 2) = x 2 + 5 x - 2 E. 9. Laske polynomien p(x) = 3 x 2 – 2 x + 1 ja q(x) = -x 2 + 2 x – 1 erotus p(x) – q(x) = (3 x 2 – 2 x + 1) – (-x 2 + 2 x – 1) = 3 x 2 – 2 x + 1 + x 2 – 2 x + 1 = 4 x 2 – 4 x + 2

POLYNOMIEN KERTOLASKU E. 10. Laske a) – 3 x 2 4 x 3 = -12 x 5 b) 4 5 x - 10 x = 20 x – 10 x = 10 x c) 4(3 x – 2) =12 x - 8 d) 4 x(2 x + 2) =8 x 2 + 8 x e) (2 x – 1) (3 x + 2) =6 x 2 + 4 x – 3 x – 2 = 6 x 2 + x - 2

POLYNOMIN JAKAMINEN MONOOMILLA Jokainen polynomin termi jaetaan monomilla E. 11. Laske

Tekijöihin jako Esimerkkejä Jaa tekijöihin 6 x + 12 =6(x + 2) 4 x 2 - 12 x =4 x(x -3)

5. 2. Binomin laskusääntöjä E. 1. 5. 2. 1. Summan ja erotuksen tulo a) (x + 2) (x – 2) = x 2 – 22 (a + b)(a – b) = a 2 – b 2 = x 2 – 4 b) (y - 4) (y + 4) = y 2 – 42 = y 2 - 16 c) (3 x - 5) (3 x + 5) = (3 x)2 – 52 = 9 x 2 - 25 d) (x 2 + 3) (x 2 – 3) = (x 2)2 – 32 = x 4 - 9 e) (3 + x) (x – 3) = (x + 3)(x – 3) = x 2 - 9 f) 4(x + 1) (x – 1) = 4(x 2 – 1) = 4 x 2 - 4

a 2 – b 2 = (a+b)(a – b) E. 2. Jaa tekijöihin a) x 2 – 9 = x 2 – 32 = (x + 3)(x -3) b) 4 x 2 – 25 = (2 x)2 – 52 = (2 x – 5)(2 x + 5) c) x 4 – 4 x 2 = x 2(x 2 -4) = x 2(x + 2)(x – 2)

E. 3. Poista neliöjuuret nimittäjästä

BINOMIN NELIÖ (a + b)2 = a 2 + 2 ab + b 2 (a - b)2 = a 2 - 2 ab + b 2 E. 4. a) ( x + 3)2 = x 2 + 2 x 3 + 32 = x 2 + 6 x + 9 b) ( x - 4)2 = x 2 - 2 x 4 + 42 = x 2 - 8 x + 16 c) (3 x + 1)2 = (3 x)2 - 2 3 x 1 + 12 = 9 x 2 - 6 x + 1 d) ( - ½x + 5)2 = (5 - ½x)2 = 52 - 2 5 ½x + (½x)2 = 25 - 5 x + ¼ x 2 = ¼ x 2 – 5 x +25

a 2 + 2 ab + b 2 = (a + b)2 a 2 - 2 ab + b 2 = (a - b)2 E. 5. Jaa tekijöihin esittämällä binomin neliönä a) x 2 + 8 x + 16 = x 2 + 2 x 4 + 4 2 = (x + 4)2 b) x 2 + 20 x + 100 = x 2 + 2 x 10 + 102 = (x + 10)2 c) 4 x 2 + 12 x + 9 = (2 x)2 + 2 2 x 3 + 32 = (2 x + 3)2

Neliöjuuren määritelmän käyttöä Luvun a neliöjuuri: Osoita likiarvoja käyttämättä, että i) >0 ii) = juurrettava i) & ii) => väite

6. 1. 1. Polynomifunktion perusmuoto E. 1. p(x) = (x – 3)(3 x – 4)2(x + 3) = (x – 3) (x + 3)(3 x – 4)2 = (x 2 – 9)(9 x 2 – 24 x + 16) = 9 x 4 – 24 x 3 + 16 x 2 - 81 x 2 + 216 x -144 = 9 x 4 – 24 x 3 - 65 x 2 + 216 x -144 (perusmuoto) asteluku: 4 aste myös: 1 + 2 + 1 = 4 laskemalla yhteen tulon tekijöiden asteet

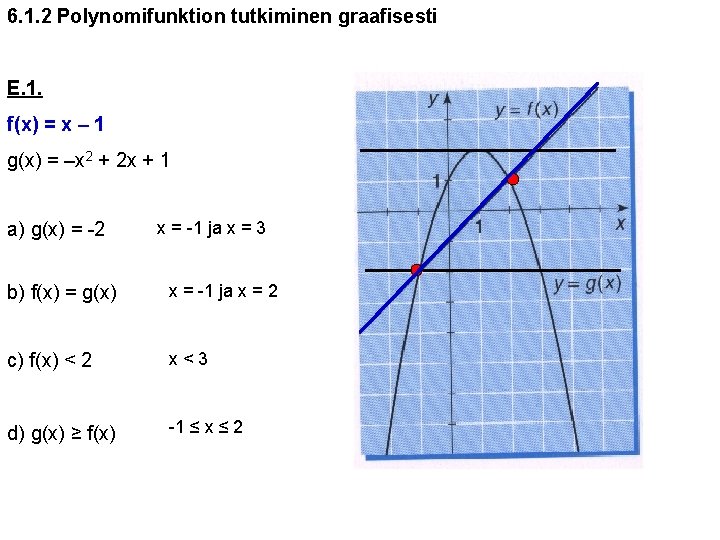
6. 1. 2 Polynomifunktion tutkiminen graafisesti E. 1. f(x) = x – 1 g(x) = –x 2 + 2 x + 1 a) g(x) = -2 x = -1 ja x = 3 b) f(x) = g(x) x = -1 ja x = 2 c) f(x) < 2 x<3 d) g(x) ≥ f(x) -1 ≤ x ≤ 2

6. 1. 3. Polynomifunktio matemaattisena mallina E. 1. Tuotteiden hinta riippuu lineaarisesti niiden hinnasta Kuukausittainen menekki astioille kuukaudessa: Yksikköhinta menekki a) f, joka ilmoittaa astioiden menekin hinnasta 10 150 f(x) = kx + b 15 110 f(10) = 150 f(15) = 110 (-1) b) Mikä on funktion määrittelyehto Hinta positiivinen => x > 0 Menekki positiivinen: 5 k = -40 10(-8) + b = 150 k = -8 b = 230 -8 x + 230 > 0 -8 x > -230 x < 28, 75 f(x) = -8 x + 230 0 < x < 28, 75

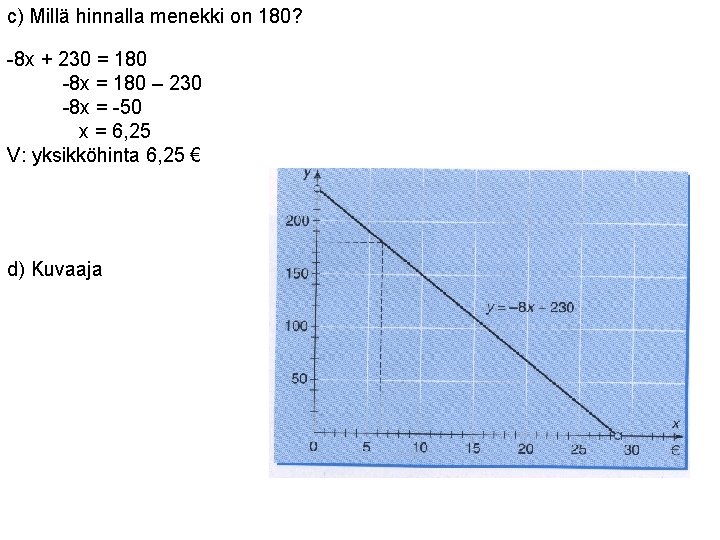
c) Millä hinnalla menekki on 180? -8 x + 230 = 180 -8 x = 180 – 230 -8 x = -50 x = 6, 25 V: yksikköhinta 6, 25 € d) Kuvaaja