3 2 Correlation Linear relations are important because

3. 2 Correlation Linear relations are important because, when we discuss the relationship between two quantitative variables, a straight line is a simple pattern that is quite common. A strong linear relationship has points that lie close to a straight line. A weak linear relationship has points that are widely scattered about a line.

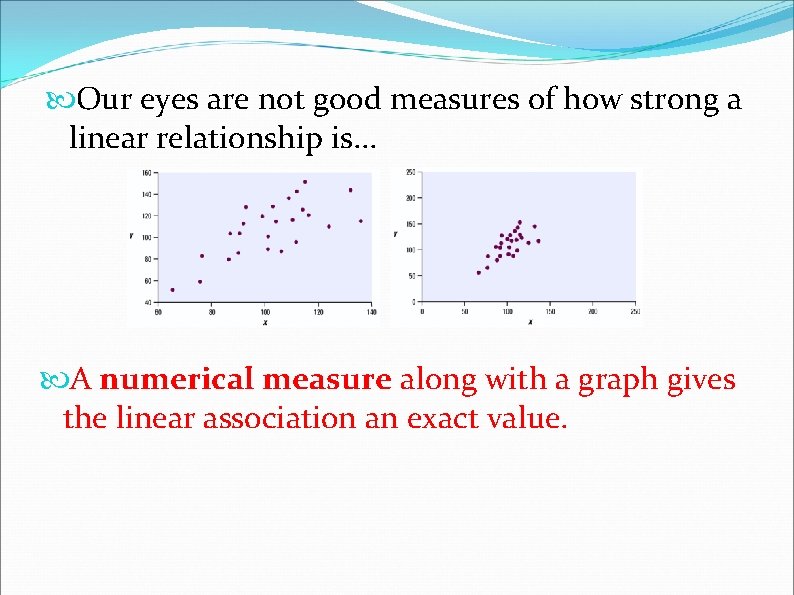
Our eyes are not good measures of how strong a linear relationship is. . . A numerical measure along with a graph gives the linear association an exact value.

In words, standardize each value, multiply corresponding standardized values, add them together, and divide by n-1

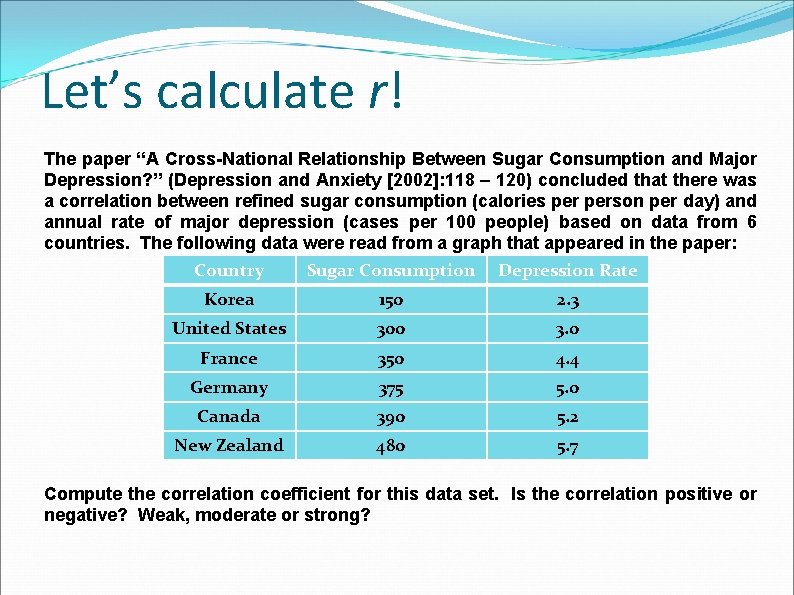
Let’s calculate r! The paper “A Cross-National Relationship Between Sugar Consumption and Major Depression? ” (Depression and Anxiety [2002]: 118 – 120) concluded that there was a correlation between refined sugar consumption (calories person per day) and annual rate of major depression (cases per 100 people) based on data from 6 countries. The following data were read from a graph that appeared in the paper: Country Sugar Consumption Depression Rate Korea 150 2. 3 United States 300 3. 0 France 350 4. 4 Germany 375 5. 0 Canada 390 5. 2 New Zealand 480 5. 7 Compute the correlation coefficient for this data set. Is the correlation positive or negative? Weak, moderate or strong?

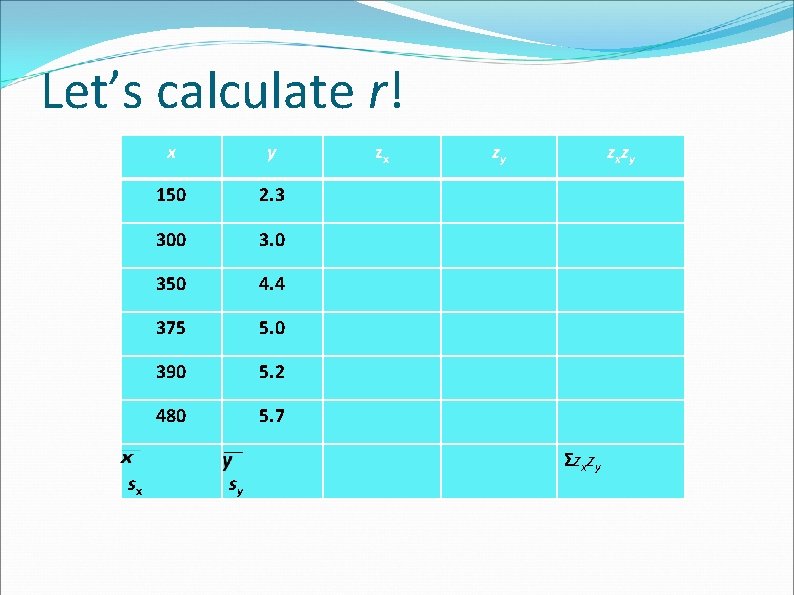
Let’s calculate r! sx x y 150 2. 3 300 3. 0 350 4. 4 375 5. 0 390 5. 2 480 5. 7 sy zx zy Σzxzy

Facts about Correlation makes no distinction between explanatory and response variables. Correlation requires that both variables be quantitative. r doesn't change when we change the units of measurement of x, y, or both. r is positive when the association is positive and is negative when the association is negative. The correlation r is always a number between -1 and 1. Values of r near 0 indicate a very weak linear relationship. The strength of the linear relationship increases as r moves away from 0 toward either -1 or 1. Correlation measures strength of linear relationships only. Like mean and standard deviation, the correlation is not resistant. Correlation is not a complete summary of two-variable data. You should give the means and standard deviations of both x and y along with the correlation.

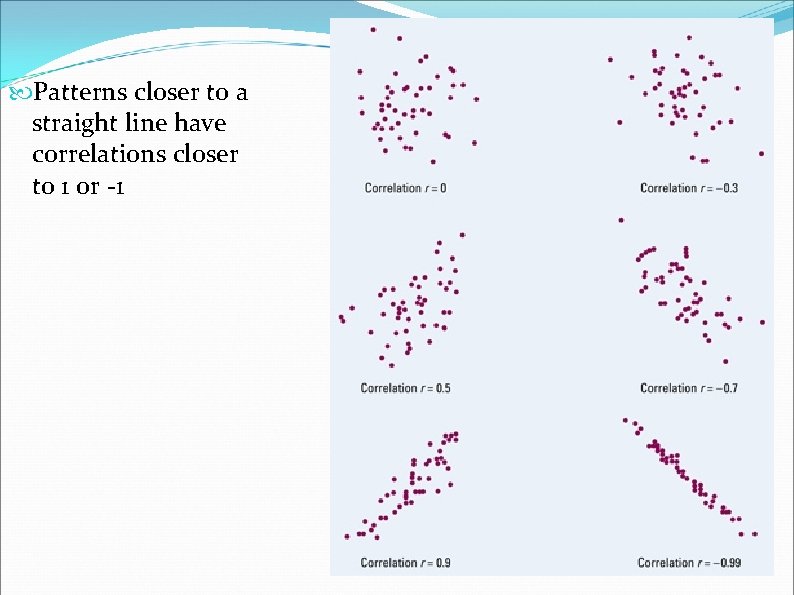
Patterns closer to a straight line have correlations closer to 1 or -1