3 2 Algoritmo di Moore per la minimizzazione

3. 2 Algoritmo di Moore per la minimizzazione dei lavori in ritardo

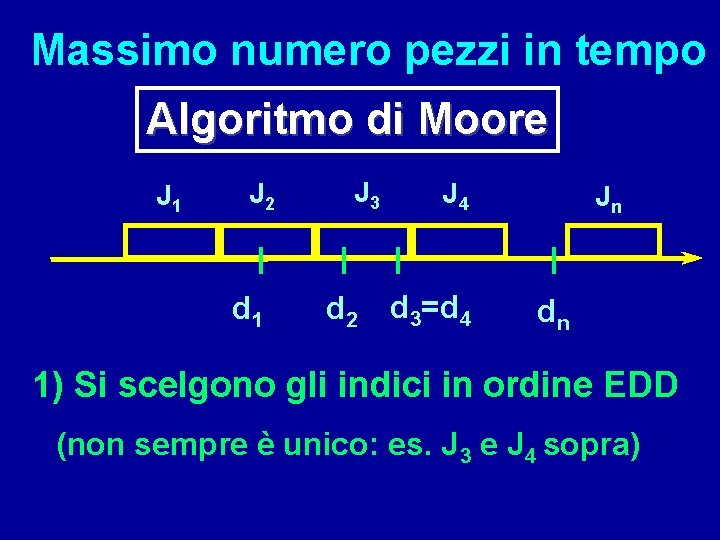
Massimo numero pezzi in tempo Algoritmo di Moore J 1 J 2 d 1 J 3 d 2 J 4 d 3=d 4 Jn dn 1) Si scelgono gli indici in ordine EDD (non sempre è unico: es. J 3 e J 4 sopra)

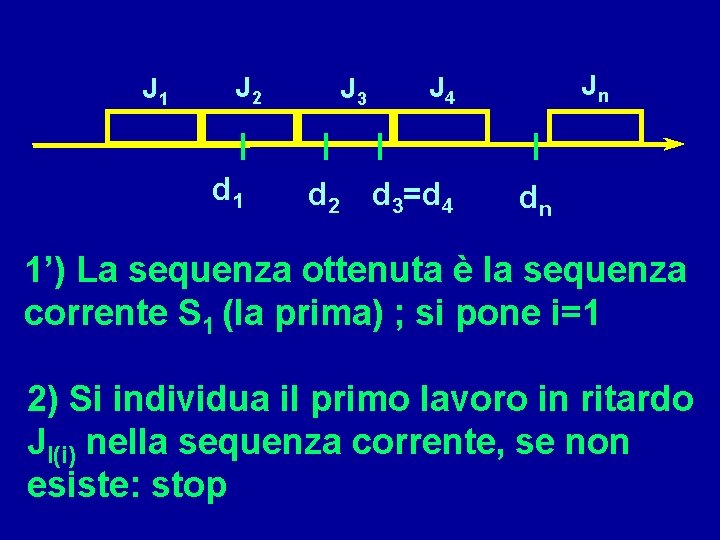
J 1 J 2 d 1 J 3 d 2 Jn J 4 d 3=d 4 dn 1’) La sequenza ottenuta è la sequenza corrente S 1 (la prima) ; si pone i=1 2) Si individua il primo lavoro in ritardo Jl(i) nella sequenza corrente, se non esiste: stop

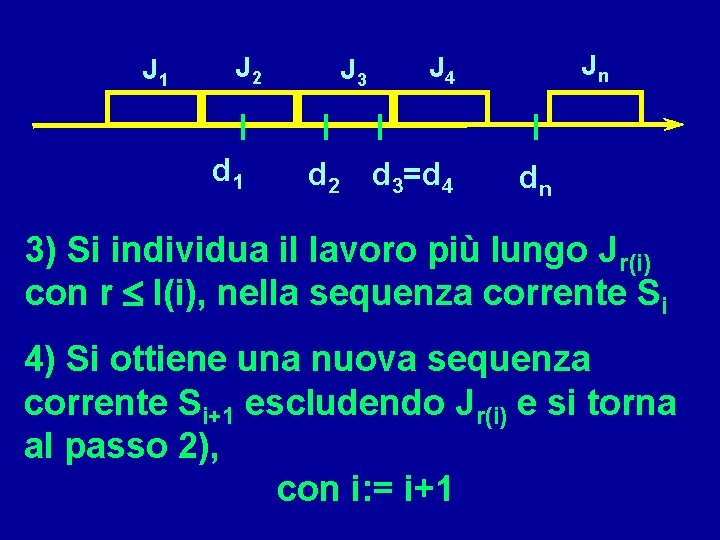
J 1 J 2 d 1 J 3 d 2 Jn J 4 d 3=d 4 dn 3) Si individua il lavoro più lungo Jr(i) con r l(i), nella sequenza corrente Si 4) Si ottiene una nuova sequenza corrente Si+1 escludendo Jr(i) e si torna al passo 2), con i: = i+1

Traduzione logica dell’intuizione Moore costruisce una sequenza con il massimo numero di lavori terminati in tempo e con il minimo tempo totale di processamento Sn Moore e’ ottima. s. K : = { i 1… ik } indici di una generica sequenza dei primi k lavori Nk : = massimo numero di lavori in tempo, rispetto a tutte le possibili Sk IP d 1 d 2 … dn ( i lavori sono ordinati secondo EDD )

Sk di Moore e’ tale che: - il numero di lavori processati in tempo e’ pari ad Nk - il tempo di processamento totale e’ minimo Praticamente Moore trova l’ottimo per i primi k lavori Dimostriamo per INDUZIONE che Sn e’ ottima • S 1 e’ banalmente ottima. • Sk assumiamola ottima. • Sk+1 e’ ottima?

• Sk+1 e’ ottima? Costruiamo la sequenza Sk+1 a partire da Sk - se jk+1 e’ processato in tempo ottengo ancora una sequenza ottima, in cui i lavori che arrivano in tempo sono ( Nk + 1 ). - se jk+1 non e’ processato in tempo, elimino il lavoro con tempo di processamento più lungo, fra gli ( Nk + 1 ). Ottengo una sequenza di k+1 lavori, di cui Nk+1 = Nk arrivano in tempo, con tempo di processamento totale minimo.

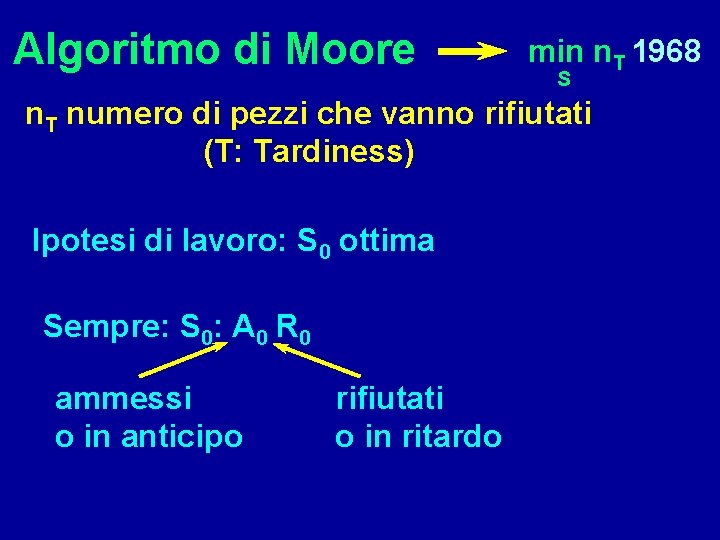
Algoritmo di Moore min n. T 1968 S n. T numero di pezzi che vanno rifiutati (T: Tardiness) Ipotesi di lavoro: S 0 ottima Sempre: S 0: A 0 R 0 ammessi o in anticipo rifiutati o in ritardo

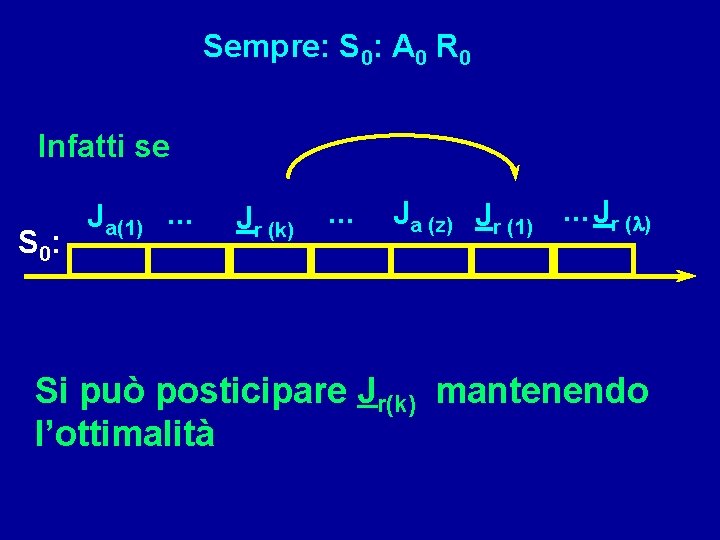
Sempre: S 0: A 0 R 0 Infatti se S 0: Ja(1). . . Jr (k) . . . Ja (z) Jr (1). . . Jr (l) Si può posticipare Jr(k) mantenendo l’ottimalità

S 0 : A 0 R 0 scelti gli indici dei lavori secondo una qualsiasi S EDD i<j di dj Si può sempre riordinare A 0 come la EDD scelta: h<k a(h) < a(k) Infatti in A 0: Lmax 0, inoltre: EDD Il riordino può essere necessario solo se $ di = dj min Lmax S

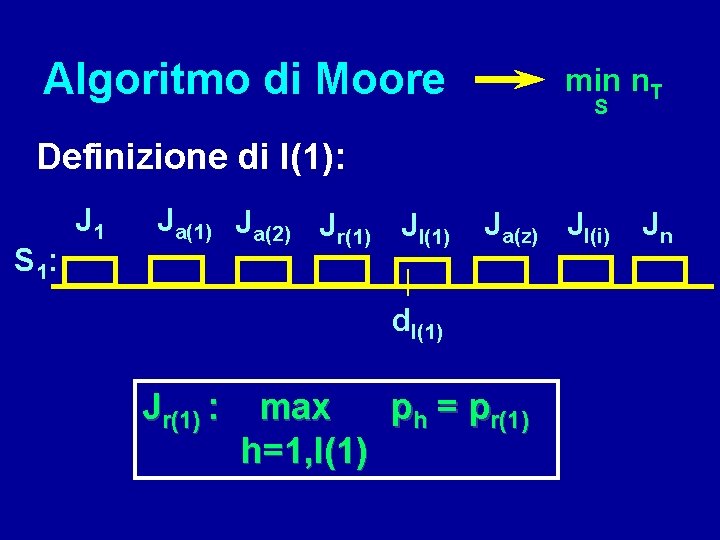
Algoritmo di Moore min n. T S Definizione di l(1): S 1: J 1 Ja(1) Ja(2) Jr(1) Jl(1) Ja(z) Jl(i) Jn dl(1) Jr(1) : max ph = pr(1) h=1, l(1)

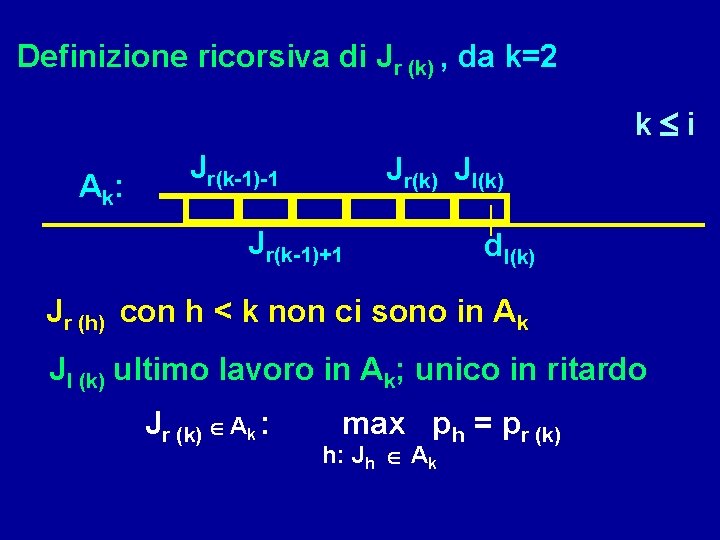
Definizione ricorsiva di Jr (k) , da k=2 k i A k: Jr(k-1)-1 Jr(k) Jl(k) Jr(k-1)+1 dl(k) Jr (h) con h < k non ci sono in Ak Jl (k) ultimo lavoro in Ak; unico in ritardo Jr (k) Ak : max ph = pr (k) h: Jh Ak

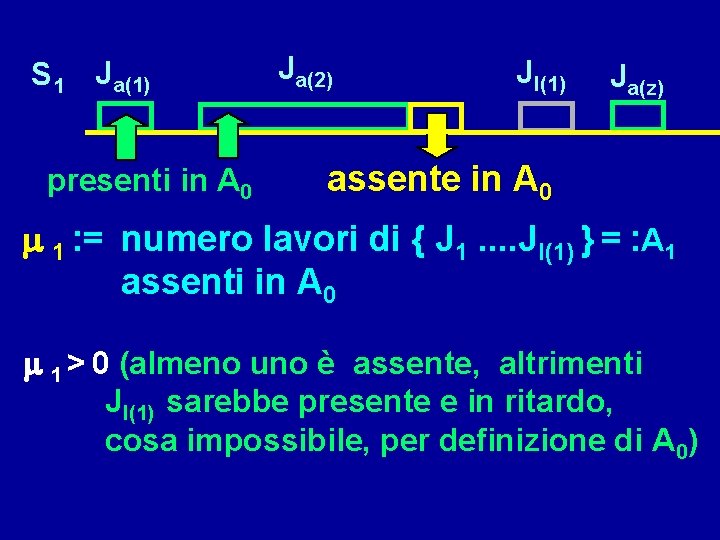
S 1 Ja(1) presenti in A 0 Ja(2) Jl(1) Ja(z) assente in A 0 m 1 : = numero lavori di { J 1. . Jl(1) } = : A 1 assenti in A 0 m 1 > 0 (almeno uno è assente, altrimenti Jl(1) sarebbe presente e in ritardo, cosa impossibile, per definizione di A 0)

Algoritmo di Moore Jq(1) : max q(1) l(1) S ph = pq (1) h=1, l(1) h ¹ a (·) l(1) pq(1) pr(1) q(1) può coincidere con r(1) min n. T Lavoro di peso massimo fra quelli in J 1. . Jl(1) assenti in A 0

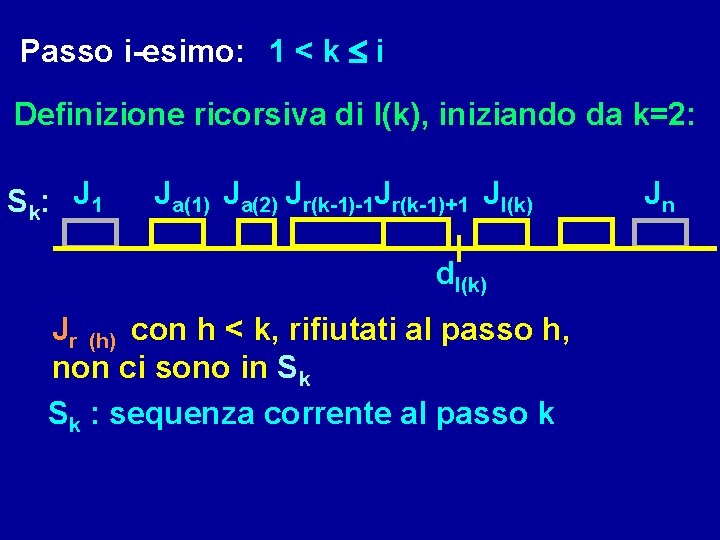
Passo i-esimo: 1 < k i Definizione ricorsiva di l(k), iniziando da k=2: S k: J 1 Ja(1) Ja(2) Jr(k-1)-1 Jr(k-1)+1 Jl(k) dl(k) Jr (h) con h < k, rifiutati al passo h, non ci sono in Sk Sk : sequenza corrente al passo k Jn

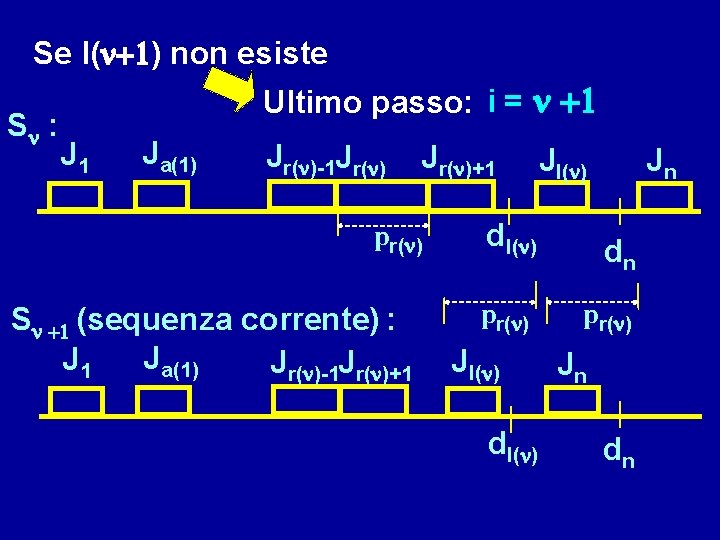
Se l(n+1) non esiste Sn : Ultimo passo: i = n +1 J 1 Ja(1) Jr(n)-1 Jr(n)+1 pr(n) Sn +1 (sequenza corrente) : Ja(1) J 1 Jr(n)-1 Jr(n)+1 Jl(n) dl(n) pr(n) Jl(n) dl(n) Jn dn pr(n) Jn dn

mk : numero lavori in J 1. . Jl(k) assenti in A 0 Jq(k) è un lavoro di peso massimo tra i mk in J 1 … Jl(k) fuori da A 0 , non già abbinati J. . J 1 l(k) Jq(k) A 0

Definizione ricorsiva di Jq(k) : Bk Jq(k) J 1. . Jl(k) => h l(k) Ï A 0 Jq(k) => A 0 È {Jq(1). . . Jq(k-1)} {Jq(1). . . Jq(k-1) } Jq(k) : pq(k) = max q(k) l(k) h l(k) Jh Bk abbinato a Jr(k) ph

Algoritmo di Moore min n. T S Passo i-esimo: a) mi ³ i Ipotesi: b) $ Jq(1). . . Jq(i) : pq(k) pr(k) Tesi: A) mi+1 ³ i +1 B) $ Jq(i+1) : pq (i+1) pr (i+1)

A) mi+1 ³ i +1 Tesi: B) $ J q(i+1) : pq (i+1) pr (i+1) Se la tesi è dimostrata, m 1 ³ 1 mn ³ n dimostra che l’algoritmo dà un ottimo

Se mi >i mi+1 ³ mi ³ i +1 Se mi = i i Jq(1). . . Jq(i), abbinati a Jr (1). . . Jr(i) q (k) l (k) pq(k) pr(k) k = 1, …, i sono esattamente tutti i lavori assenti in A 0 tra J 1. . . Jl(i)

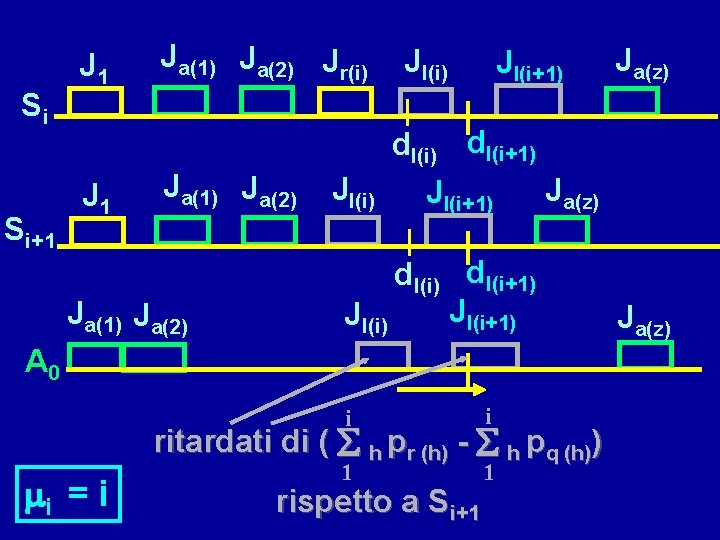
Si Si+1 J 1 Ja(1) Ja(2) Jr(i) Ja(1) Ja(2) Jl(i) Jl(i+1) dl(i+1) Ja(z) Jl(i+1) dl(i+1) Jl(i) A 0 i i 1 1 ritardati di ( å h pr (h) - å h pq (h)) mi = i Ja(z) rispetto a Si+1 Ja(z)

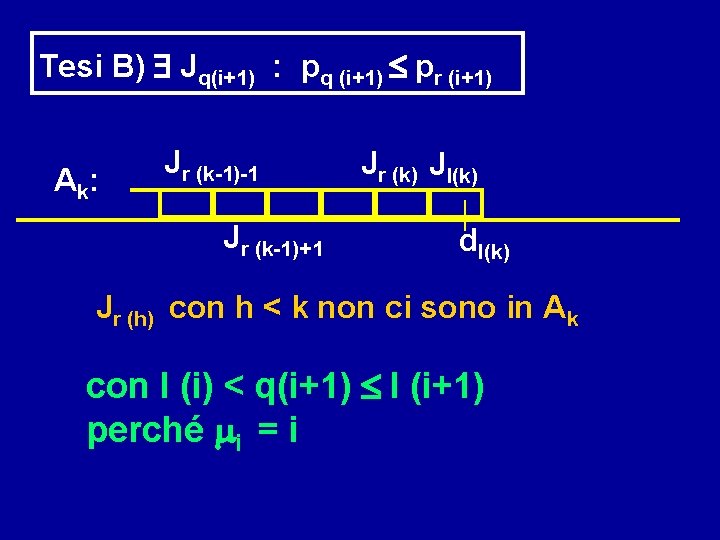
Tesi B) $ Jq(i+1) : pq (i+1) pr (i+1) A k: Jr (k-1)-1 Jr (k-1)+1 Jr (k) Jl(k) dl(k) Jr (h) con h < k non ci sono in Ak con l (i) < q(i+1) l (i+1) perché mi = i

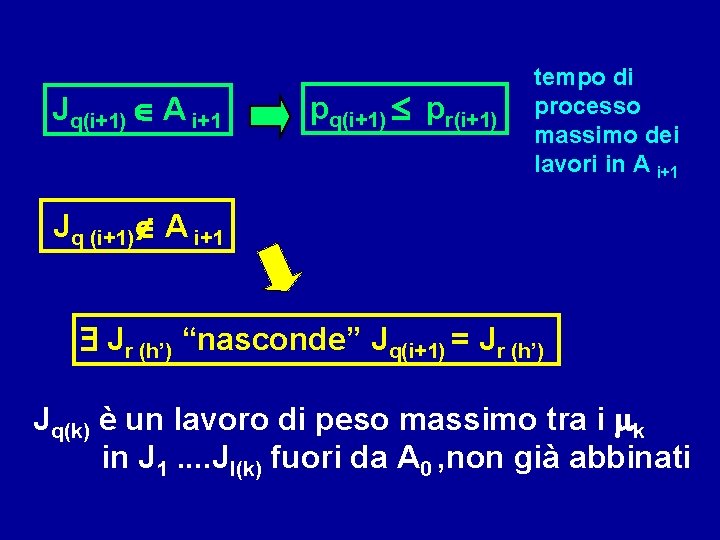
Jq(i+1) A i+1 pq(i+1) pr(i+1) tempo di processo massimo dei lavori in A i+1 Jq (i+1) A i+1 $ Jr (h’) “nasconde” Jq(i+1) = Jr (h’) Jq(k) è un lavoro di peso massimo tra i mk in J 1. . Jl(k) fuori da A 0 , non già abbinati

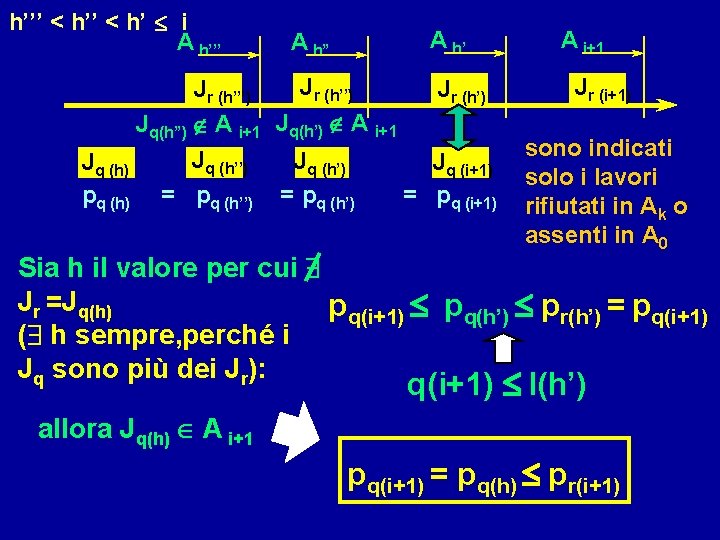
h’’’ < h’ i A h’’’ A h” Jr (h’’) Jr (h’’’) Jq(h”) A i+1 Jq(h’) A i+1 Jq (h) pq (h) Jq (h’’) = pq (h’’) Jq (h’) = pq (h’) Jr (h’) Jq (i+1) = pq (i+1) A i+1 Jr (i+1) sono indicati solo i lavori rifiutati in Ak o assenti in A 0 Sia h il valore per cui $ Jr =Jq(h) pq(i+1) pq(h’) pr(h’) = pq(i+1) ($ h sempre, perché i Jq sono più dei Jr): q(i+1) l(h’) allora Jq(h) A i+1 pq(i+1) = pq(h) pr(i+1)