3 2 1 LOADING STATISTIKA DESKRIPTIF KEMIRINGAN KERUNCINGAN

3

2

1

LOADING

STATISTIKA DESKRIPTIF KEMIRINGAN, KERUNCINGAN DISTRIBUSI DATA (UKURAN PENYEBARAN DATA)

Profil Materi Grafik Evaluasi Kemiringan Dan Keruncingan Distribusi Data Stay Logout

Wassalamualaikum Wr. Wb

Sefta Layli Uhdia Fishaum 11 7 0 4 1 1 NIM: 1 22 : n com e. s s b s A e. r o p N rd o w. f a i d Seftaly a y n u p h uda s u a l a ada “k , t a i n a n d a a d , , n s a u u r te tuj a h a s u ai r p e m b a , s d a h tek alla a h s n i at g n a m e s ”

KESIMPULAN Ada 3 jenis grafik yang dapat digunakan dalam menganalisa kemiringan atau keruncingan distribusi data. Derajat kemiringan angka 0 menunjukkan puncak normal, sedangkan derajat keruncingan angka 3 menunjukkan puncak normal.

KEMIRINGAN DISTRIBUSI DATA Merupakan derajat atau ukuran dari ketidsksimetrian (Asimetri) suatu distribusi data. Kemiringan distribusi data terdapat 3 jenis : 1. Simetris : menunjukkan letak nilai rat-rata hitung, median dan modus berhimpit(berkisar disatu titik) 2. Miring kekanan : mempunyai nilai modus paling kecil dan rata-rata hitung paling besar 3. Miring kekiri : mempunyai nilai modus paling besar dan rata-rata hitung paling kecil

Grafik Distribusi Kemiringan Simetri Miring Kekanan

Grafik Distribusi Kemiringan Miring Ke Kiri

Rumus Kemiringan derajat distribusi data(α 3) =

Question Data : 6, 7, 8, 5, 8, 88 5, 6, 7, 8, 8, 8 Diperoleh: = 1/6(5+6+7+8+8+8)=42/6=7 Median Modus • Med=1/2(7+8)=7, 5 • Mod=8

= Standar Deviasi diperoleh dari variansinya yaitu STANDAR DEVIASINYA = 1, 2

Rumus Pearson Karna α bertanda negatif maka distribusi data miring ke kiri

Rumus Momen Karna α bertanda negatif maka distribusi data, miring ke kiri

Rumus Bowley

Data : 10, 15, 20, 25, 30, 35 N=6 Q 2 = Q 1=X 1+0, 75 (X 2 -X 1) Q 2=X 3+0, 5 (X 4 -X 3) Q 1= 10+0, 75(15 -10)=53, 75 Q 2= 20+0, 5(25 -20)=102, 5 Q 3 = Q 3=X 5+0, 25 (X 6 -X 5) Q 3=30+0, 25(35 -30)=151, 25

Karena α bertanda positif, maka distribusi data miring kekanan

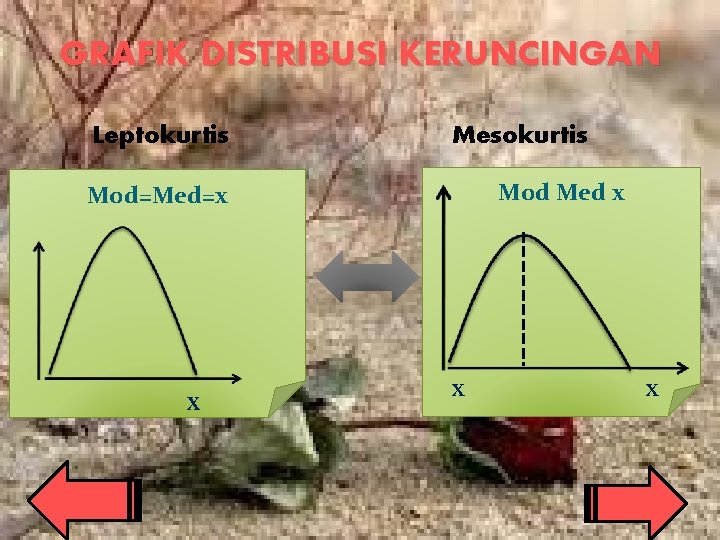
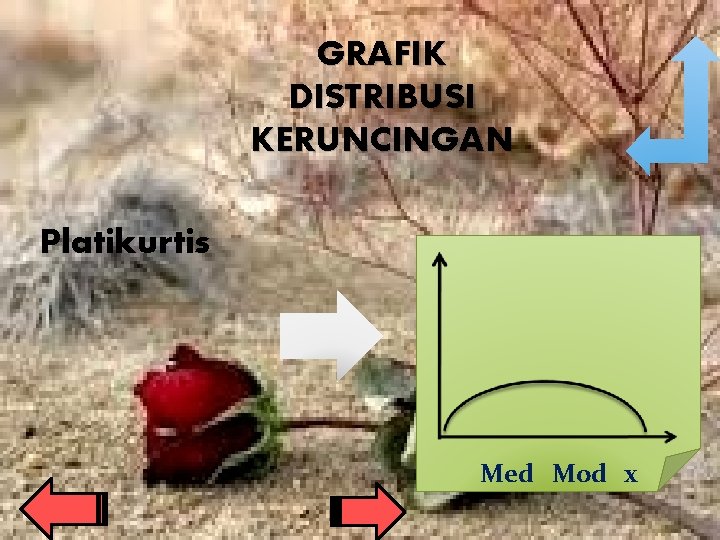
KERUNCINGAN DISTRIBUSI DATA Merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Disebut juga Kurtosis. Ada 3 jenis keruncingan data, yaitu: 1. Leptokurtis: Distribusi data yg puncaknya relatif tinggi. 2. Mesokurtis: Distribusi data yg puncaknya normal. 3. Platikurtis: Distribusi data yg puncaknya terlalu rendah atau mendatar.

GRAFIK DISTRIBUSI KERUNCINGAN Leptokurtis Mesokurtis Mod Med x Mod=Med=x X X X

GRAFIK DISTRIBUSI KERUNCINGAN Platikurtis Med Mod x

Rumus Derajat keruncingan � Data Berkelompok