3 2 1 Augmenting path algorithm Two theorems





- Slides: 23

3. 2. 1. Augmenting path algorithm Two theorems to recall: Theorem 3. 1. 10 (Berge). A matching M in a graph G is a maximum matching in G iff G has no M-augmenting path. Theorem 3. 1. 16 (König, Egerváry) If G is bipartite, then a maximum matching and a minimum vertex cover of G have the same size ( ’(G)= (G)). Augmenting path algorithm for maximum bipartite matching Input: X, Y-bigraph. Output: M, Q with |M|=|Q| Use modified breadth-first search to find augmenting paths. Initialize with empty matching and iteratively increase by 1. Produce a vertex cover of same size to certify the output. 1

3. 2. 1. Augmenting path algorithm Algorithm (Augmenting path algorithm) Input An X, Y-bigraph G, a (partial matching) M, and the set U of M-unsaturated vertices of X Idea Explore augmenting paths to all possible vertices, marking explored vertices and their predecessors, and tracking reached vertices SµX and TµY Initialization S=U and T=; Iteration If S is all marked, stop and output M and Q=T[(X-S). Otherwise, explore from an unmarked x 2 S. For any edge xy 2 E(G)-M: (1) mark y and put y in T. (2) For any edge yw 2 M, mark w and put w in S. Stop if an unsaturated y is found; report an M-augmenting path. Otherwise continue exploring in this fashion. 2

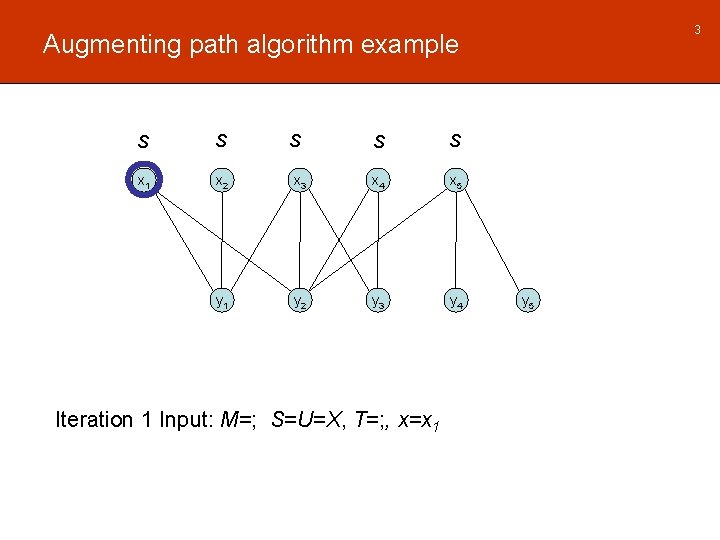
3 Augmenting path algorithm example S S x 1 x 2 y 1 S S S x 3 x 4 x 5 y 2 y 3 y 4 Iteration 1 Input: M=; S=U=X, T=; , x=x 1 y 5

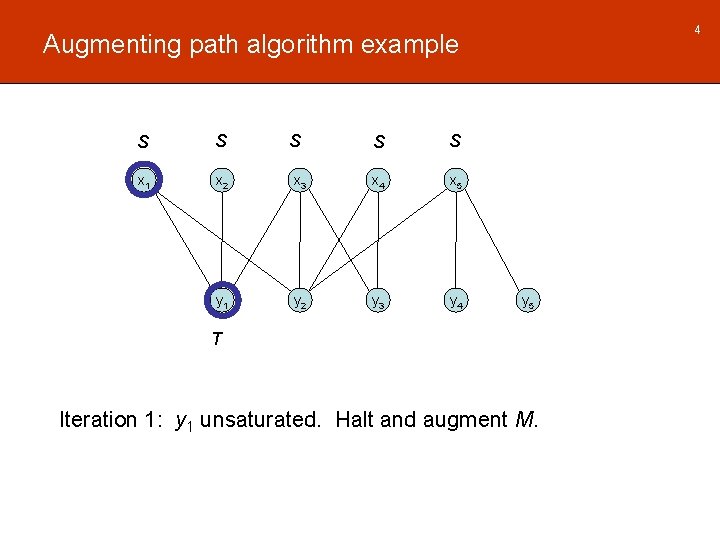
4 Augmenting path algorithm example S S x 1 x 2 y 1 S S S x 3 x 4 x 5 y 2 y 3 y 4 y 5 T Iteration 1: y 1 unsaturated. Halt and augment M.

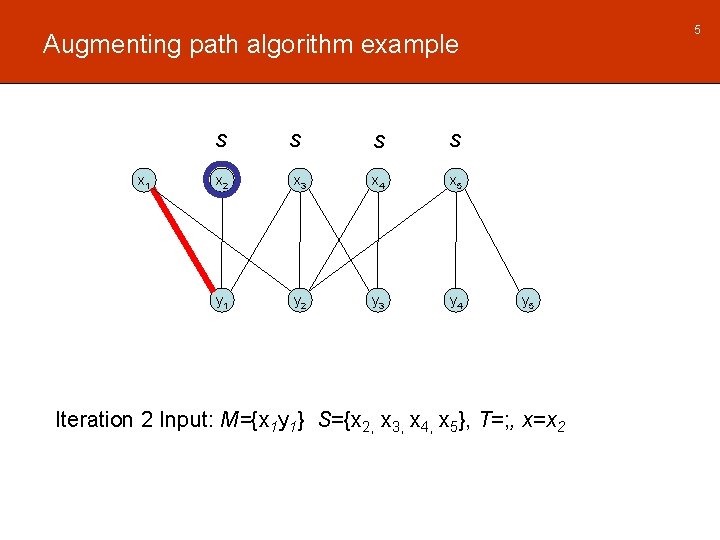
5 Augmenting path algorithm example S x 1 S S S x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 y 5 Iteration 2 Input: M={x 1 y 1} S={x 2, x 3, x 4, x 5}, T=; , x=x 2

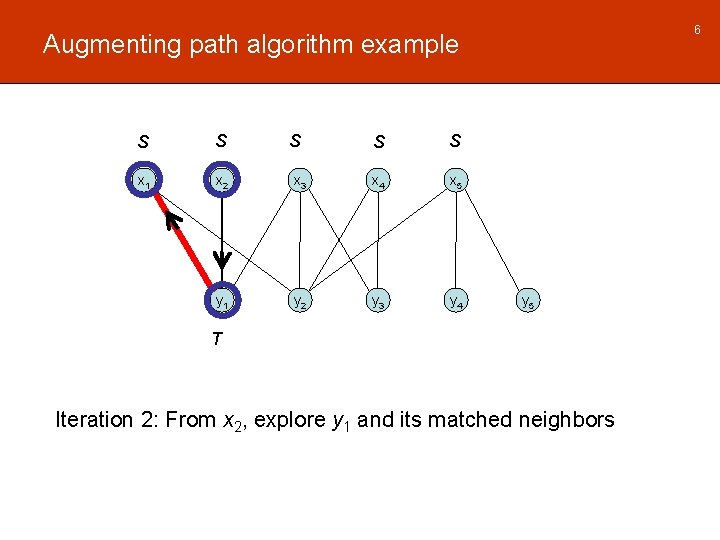
6 Augmenting path algorithm example S S x 1 x 2 y 1 S S S x 3 x 4 x 5 y 2 y 3 y 4 y 5 T Iteration 2: From x 2, explore y 1 and its matched neighbors

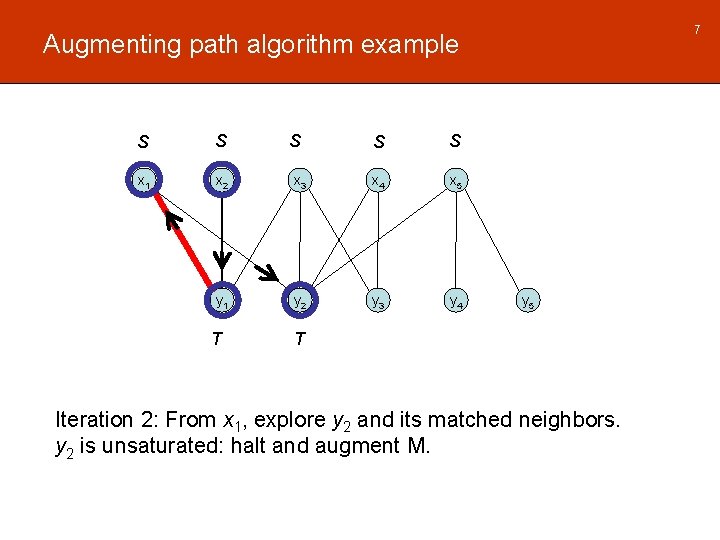
7 Augmenting path algorithm example S S x 1 x 2 y 1 T S S S x 3 x 4 x 5 y 2 y 3 y 4 y 5 T Iteration 2: From x 1, explore y 2 and its matched neighbors. y 2 is unsaturated: halt and augment M.

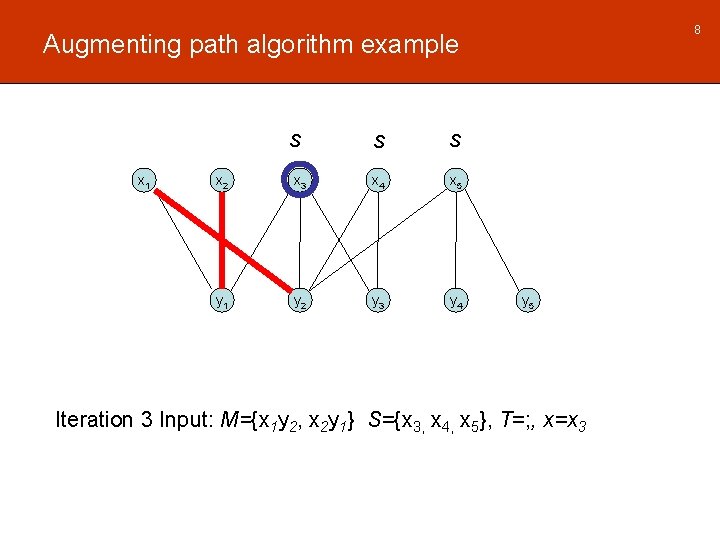
8 Augmenting path algorithm example S x 1 S S x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 y 5 Iteration 3 Input: M={x 1 y 2, x 2 y 1} S={x 3, x 4, x 5}, T=; , x=x 3

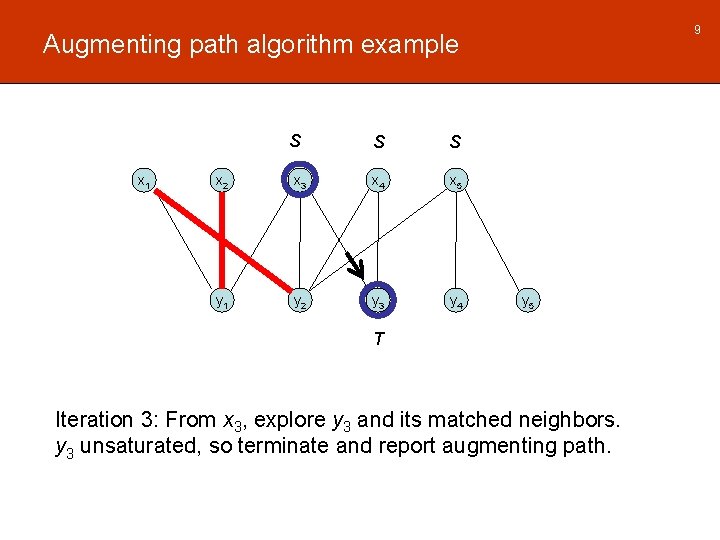
9 Augmenting path algorithm example S x 1 S S x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 y 5 T Iteration 3: From x 3, explore y 3 and its matched neighbors. y 3 unsaturated, so terminate and report augmenting path.

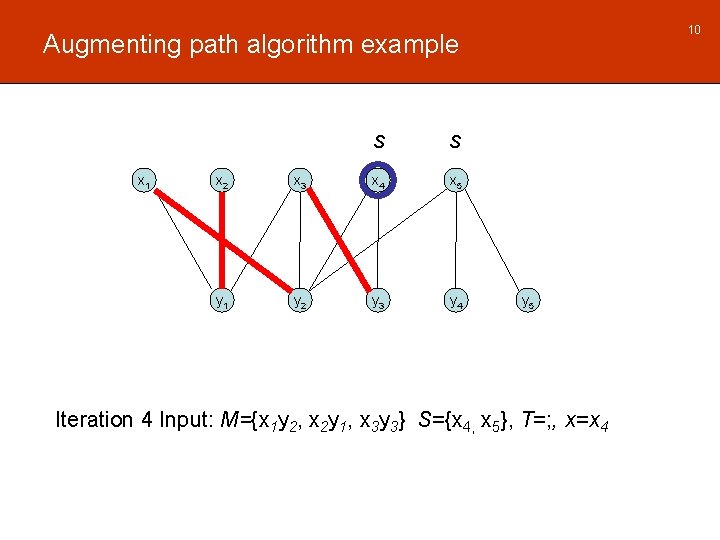
10 Augmenting path algorithm example x 1 S S x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 y 5 Iteration 4 Input: M={x 1 y 2, x 2 y 1, x 3 y 3} S={x 4, x 5}, T=; , x=x 4

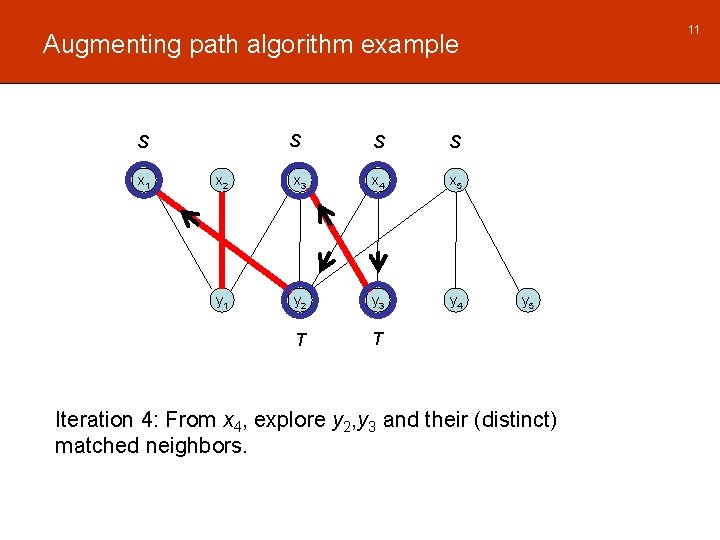
11 Augmenting path algorithm example S S x 1 S S x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 T T y 5 Iteration 4: From x 4, explore y 2, y 3 and their (distinct) matched neighbors.

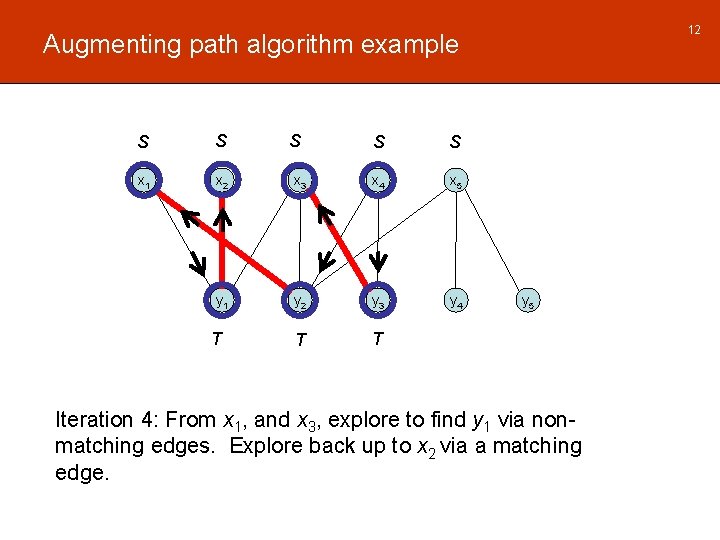
12 Augmenting path algorithm example S S x 1 x 2 y 1 T S S S x 3 x 4 x 5 y 2 y 3 y 4 T T y 5 Iteration 4: From x 1, and x 3, explore to find y 1 via nonmatching edges. Explore back up to x 2 via a matching edge.

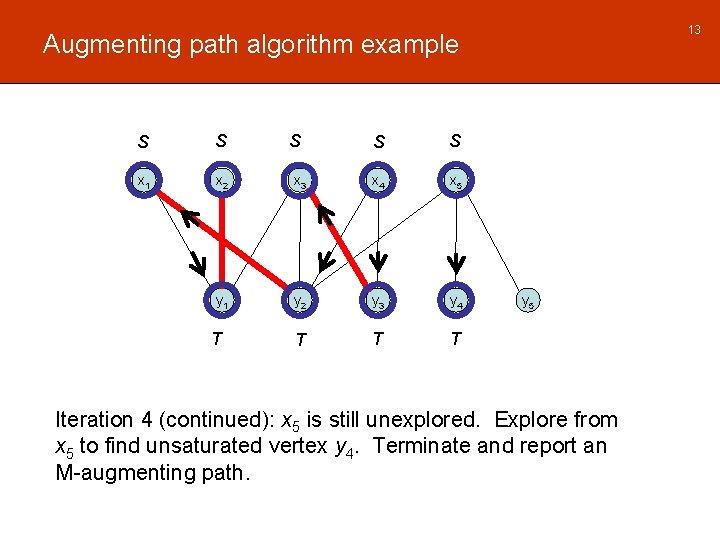
13 Augmenting path algorithm example S S x 1 x 2 y 1 T S S S x 3 x 4 x 5 y 2 y 3 y 4 T T T y 5 Iteration 4 (continued): x 5 is still unexplored. Explore from x 5 to find unsaturated vertex y 4. Terminate and report an M-augmenting path.

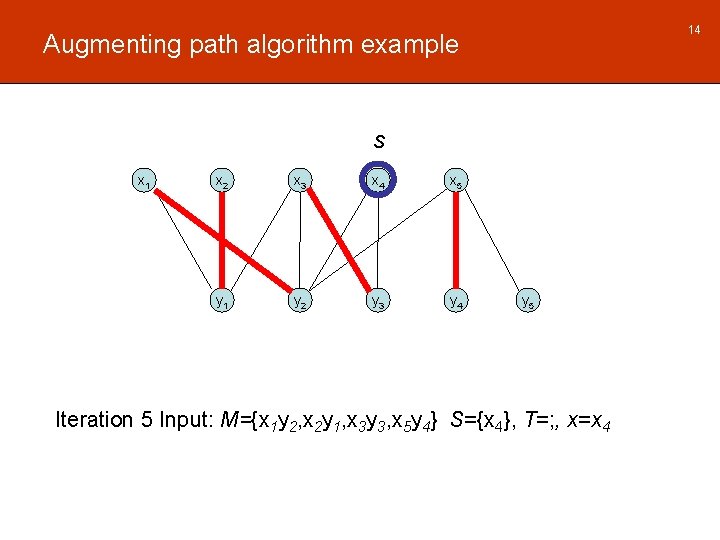
14 Augmenting path algorithm example S x 1 x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 y 5 Iteration 5 Input: M={x 1 y 2, x 2 y 1, x 3 y 3, x 5 y 4} S={x 4}, T=; , x=x 4

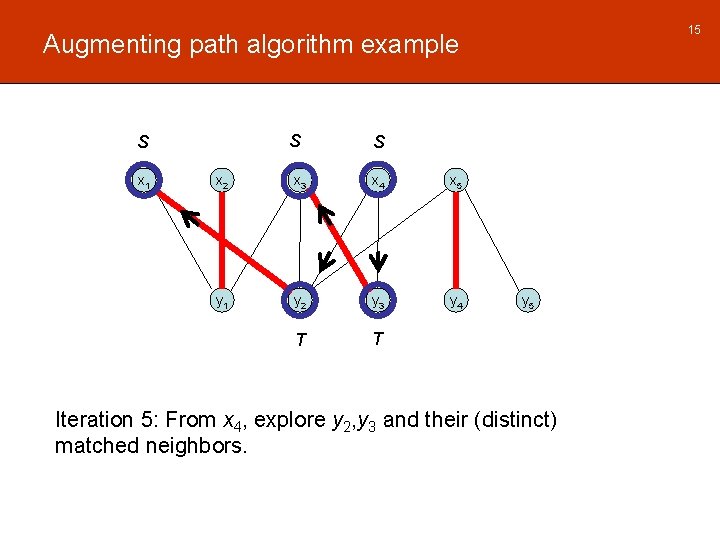
15 Augmenting path algorithm example S S x 1 S x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 T T y 5 Iteration 5: From x 4, explore y 2, y 3 and their (distinct) matched neighbors.

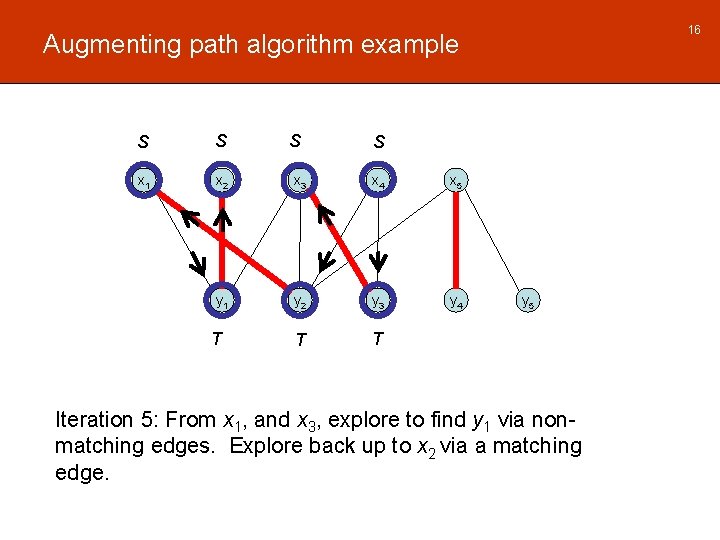
16 Augmenting path algorithm example S S x 1 x 2 x 3 x 4 x 5 y 1 y 2 y 3 y 4 T T T S S y 5 Iteration 5: From x 1, and x 3, explore to find y 1 via nonmatching edges. Explore back up to x 2 via a matching edge.

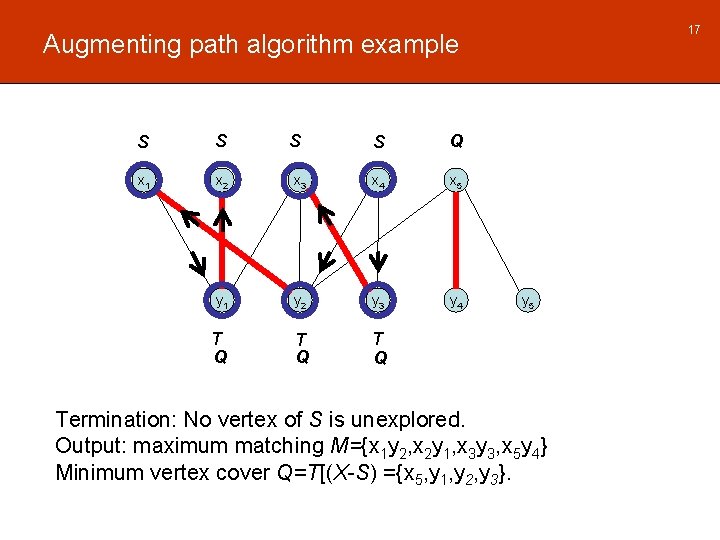
17 Augmenting path algorithm example S S x 1 x 2 S S Q x 3 x 4 x 5 y 1 y 2 y 3 y 4 T Q T Q y 5 Termination: No vertex of S is unexplored. Output: maximum matching M={x 1 y 2, x 2 y 1, x 3 y 3, x 5 y 4} Minimum vertex cover Q=T[(X-S) ={x 5, y 1, y 2, y 3}.

Maximum Weighted Transversal: A set M of n entries of an n£n, matrix, no two in the same column or row. Its weight is the sum of the entries. Cover: A pair of vectors (u, v)=(u 1, …, un; v 1, …, vn) such that every entry wi, j of the matrix satisfies wi, j · ui+vj. v u 0 0 0 6 4 4 4 3 6 4 1 1 4 3 4 5 1 4 5 3 5 9 5 6 4 7 9 8 5 3 6 8 3 w(u, v)=32 w(M)=23

3. 2. 7. Maximum Transversal = Minimum Cover 3. 2. 7. Lemma. (Duality of weighted matching and weighted cover problems) For a perfect matching M and a weighted cover (u, v) in a weighted bipartite graph G, c(u, v)¸w(M). Also, c(u, v)=w(M) iff M consists of edges xiyj such that ui+vj=wi, j. In this case, M and (u, v) are optimal. v u 0 1 2 4 4 2 1 1 4 3 1 4 5 w(u, v)=12 w(M)=12

3. 2. 9. Hungarian Algorithm (Maximum Weighted Matching/Minimum Weighted Cover) Algorithm (Hungarian Algorithm) Input An n£n matrix of nonnegative edge weights of Kn, n Idea Iteratively adjust the cover (u, v) until the equality subgraph Gu, v has a perfect matching Initialization Any cover (u, v), such as ui=maxi wi, j and vj=0 Iteration Find a maximum matching M in Gu, v. If M is a perfect matching, stop and output M and (u, v) as a maximum weight matching and minimum weight cover. Otherwise: Let = smallest excess in Gu, v of an edge from X-R to Y-T. Replace uià ui- for all xi 2 X-R. Replace vjà vj+ for all yj 2 Y-T. Form the new equality subgraph Gu, v and repeat. 20

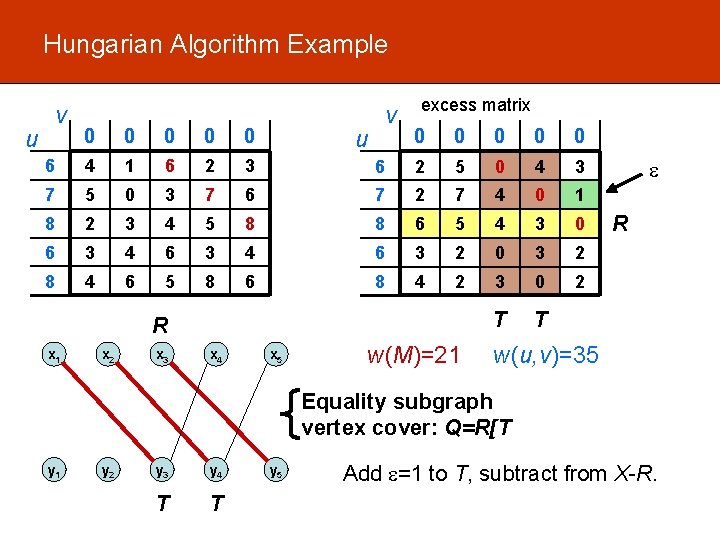
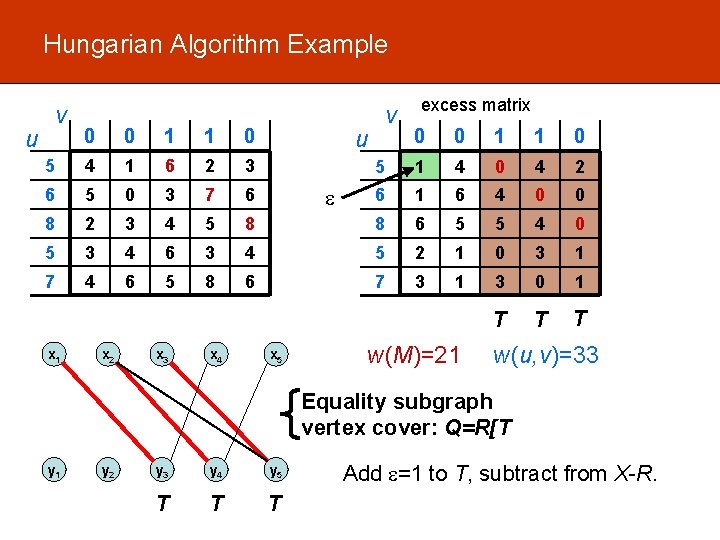
Hungarian Algorithm Example v 0 0 0 6 4 1 6 2 3 7 5 0 3 7 8 2 3 4 6 3 4 8 4 6 u v excess matrix 0 0 0 6 2 5 0 4 3 6 7 2 7 4 0 1 5 8 8 6 5 4 3 0 6 3 4 6 3 2 0 3 2 5 8 6 8 4 2 3 0 2 T T u R x 1 x 2 x 3 x 4 x 5 w(M)=21 R w(u, v)=35 Equality subgraph vertex cover: Q=R[T y 1 y 2 y 3 y 4 T T y 5 Add =1 to T, subtract from X-R.

Hungarian Algorithm Example v 0 0 1 1 0 5 4 1 6 2 3 6 5 0 3 7 6 8 2 3 4 5 5 3 4 6 7 4 6 5 u x 1 x 2 x 3 v excess matrix 0 0 1 1 0 5 1 4 0 4 2 6 1 6 4 0 0 8 8 6 5 5 4 0 3 4 5 2 1 0 3 1 8 6 7 3 1 3 0 1 T T T x 4 u x 5 w(M)=21 w(u, v)=33 Equality subgraph vertex cover: Q=R[T y 1 y 2 y 3 y 4 y 5 T T T Add =1 to T, subtract from X-R.

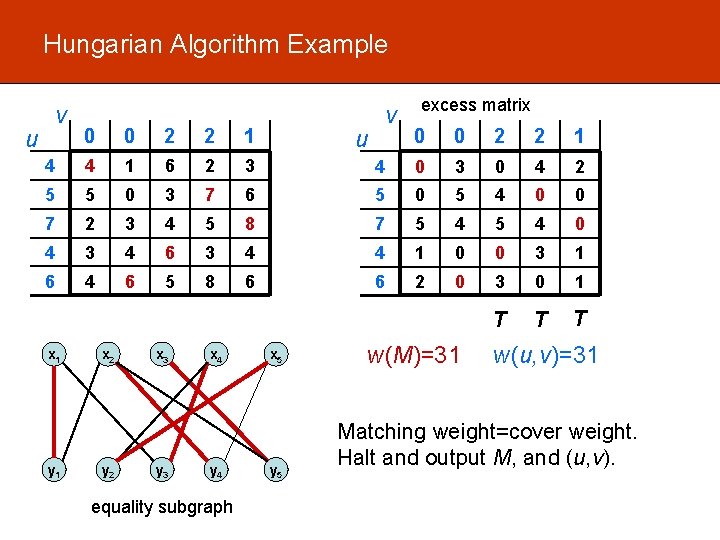
Hungarian Algorithm Example v 0 0 2 2 1 4 4 1 6 2 3 5 5 0 3 7 7 2 3 4 4 3 4 6 u x 1 y 1 x 2 y 2 v excess matrix 0 0 2 2 1 4 0 3 0 4 2 6 5 0 5 4 0 0 5 8 7 5 4 0 6 3 4 4 1 0 0 3 1 5 8 6 6 2 0 3 0 1 T T T x 3 y 3 x 4 y 4 equality subgraph u x 5 y 5 w(M)=31 w(u, v)=31 Matching weight=cover weight. Halt and output M, and (u, v).