3 1 Symmetry Symmetry All Around Us Symmetry

  • Slides: 21
Download presentation
3 -1 Symmetry

3 -1 Symmetry

Symmetry All Around Us Symmetry at the Beach Line Symmetry & Rotational Symmetry -

Symmetry All Around Us Symmetry at the Beach Line Symmetry & Rotational Symmetry - All you need to Know + Symmetry in the World, Symmetry Games, symmetry of the face, Symmetry Quiz and Worksheets

Point Symmetry Two distinct points P and P’ are symmetric with respect to a

Point Symmetry Two distinct points P and P’ are symmetric with respect to a point, M, if and only if M is the midpoint of PP’. Point M is symmetric with respect to itself. A figure with point symmetry can be turned about a center point and, in less than a full turn, the image coincides with the original figure.

Examples

Examples

Symmetry with Respect to the Origin The graph of a relation S is symmetric

Symmetry with Respect to the Origin The graph of a relation S is symmetric with respect to the origin iff (a, b) Є S implies that ( -a, -b) Є S. A function f(x) has a graph that is symmetric with respect to the origin iff f(-x) = -f(x).

Example of Symmetry with Respect to the Origin

Example of Symmetry with Respect to the Origin

Example: Determine whether the graph of f(x) = -7 x 5 + 8 x

Example: Determine whether the graph of f(x) = -7 x 5 + 8 x is symmetric with respect to the origin.

Example: Determine whether the graph of f(x) = x 2 - 2 x -

Example: Determine whether the graph of f(x) = x 2 - 2 x - 1 is symmetric with respect to the origin.

Line of Symmetry Two distinct points P and P’ are symmetric with respect to

Line of Symmetry Two distinct points P and P’ are symmetric with respect to a line ℓ iff ℓ is the perpendicular bisector of PP’. A point P is symmetric to itself with respect to the line ℓ iff P is on ℓ.

Examples of Line Symmetry

Examples of Line Symmetry

Symmetry with Respect to … the x-axis (a, -b) Є S iff (a, b)

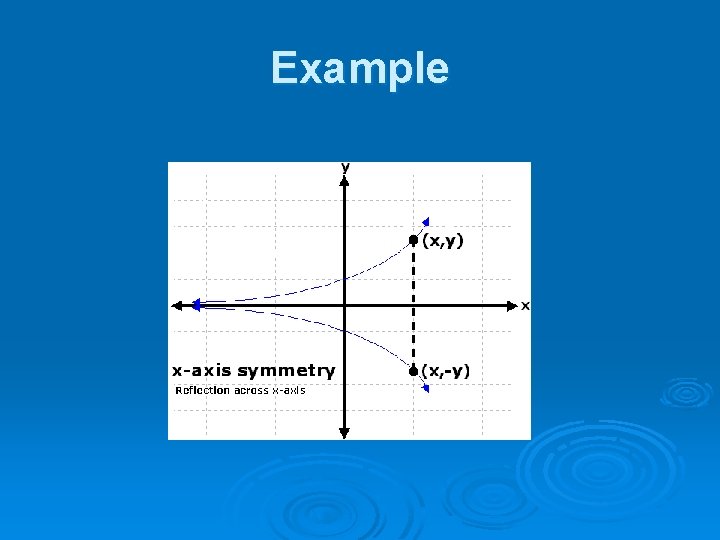
Symmetry with Respect to … the x-axis (a, -b) Є S iff (a, b) Є S The graph of x = y 2 – 4 (0, 2) and (0, -2) are on the graph

Example

Example

Symmetry with Respect to … the y-axis (-a, b) Є S iff (a, b)

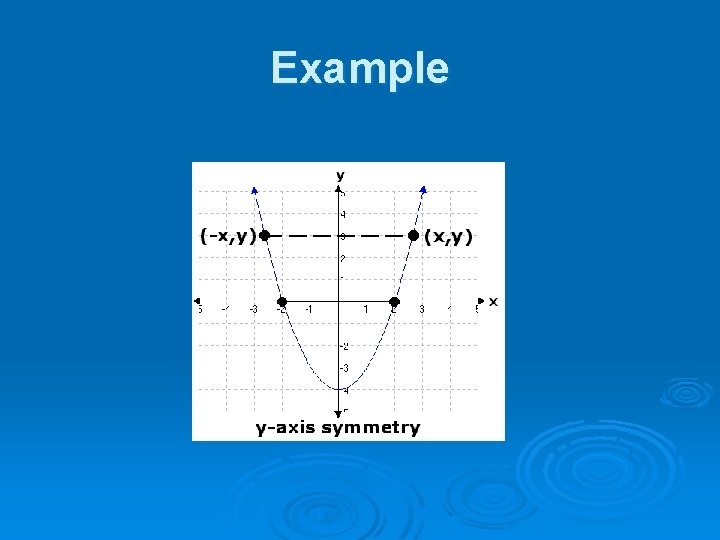
Symmetry with Respect to … the y-axis (-a, b) Є S iff (a, b) Є S The graph of y = x 2 - 4 (2, 0) and (-2, 0) are on the graph

Example

Example

Symmetry with Respect to … the line y = x (b, a) Є S

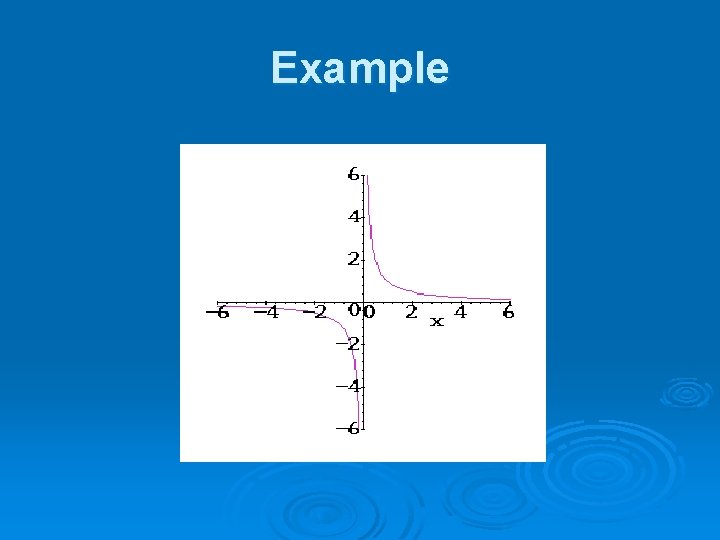
Symmetry with Respect to … the line y = x (b, a) Є S iff (a, b) Є S The graph of xy = 6 (2, 3) and (3, 2) are on the graph

Example

Example

Symmetry with Respect to … the line y = -x (-b, -a) Є S

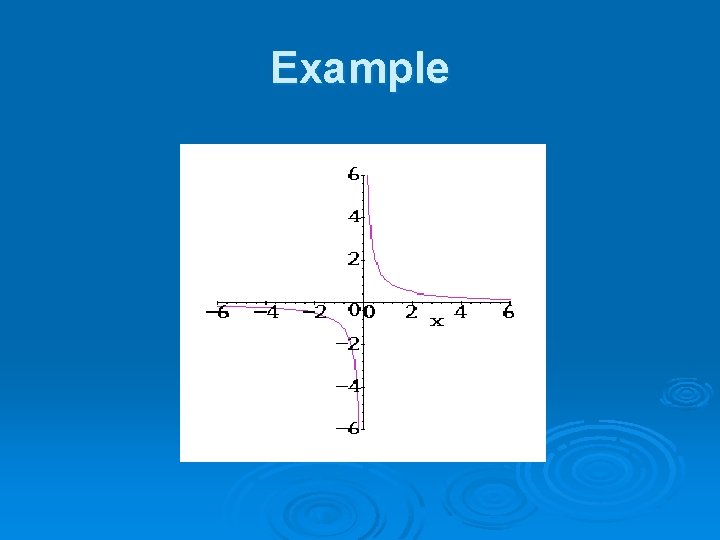
Symmetry with Respect to … the line y = -x (-b, -a) Є S iff (a, b) Є S The graph of xy = 6 (3, 2) and (-2, -3) are on the graph

Example

Example

Even Functions that are symmetric with respect to the y-axis are even. All exponents

Even Functions that are symmetric with respect to the y-axis are even. All exponents are even.

Odd Functions that are symmetric with respect to the origin are odd functions. All

Odd Functions that are symmetric with respect to the origin are odd functions. All exponents are odd.

Determine whether the graph of x + y 2 = 1 is symmetric with

Determine whether the graph of x + y 2 = 1 is symmetric with respect to the x-axis, y-axis, the line y = x, the line y = -x, or none of these.

Symmetry Ahhhh Isnt symmetry wonderful Symmetry is allSymmetry Ahhhh Isnt symmetry wonderful Symmetry is all
Symmetry Line Symmetry n Shape has line symmetrySymmetry Line Symmetry n Shape has line symmetry
Plane Symmetry Plane Symmetry A plane of symmetryPlane Symmetry Plane Symmetry A plane of symmetry
Symmetry Monarch butterfly bilateral symmetry mirror symmetry WheneverSymmetry Monarch butterfly bilateral symmetry mirror symmetry Whenever
Symmetry Concept 39 symmetry line of symmetry rotationalSymmetry Concept 39 symmetry line of symmetry rotational
Symmetry Monarch butterfly bilateral symmetry mirror symmetry 153Symmetry Monarch butterfly bilateral symmetry mirror symmetry 153
symmetry line of symmetry rotational symmetry center ofsymmetry line of symmetry rotational symmetry center of
SYMMETRY LINE SYMMETRY A line symmetry occurs inSYMMETRY LINE SYMMETRY A line symmetry occurs in
Symmetry Line Symmetry A figure has line symmetrySymmetry Line Symmetry A figure has line symmetry
All Around the Kitchen All around the kitchenAll Around the Kitchen All around the kitchen
Formulae All Around Us Formulae are all aroundFormulae All Around Us Formulae are all around
Symmetry in Nature Symmetry Can Be Found AllSymmetry in Nature Symmetry Can Be Found All
Puppets around the world All around the worldPuppets around the world All around the world
Puppets around the world All around the worldPuppets around the world All around the world
New Years Day Around the World All aroundNew Years Day Around the World All around
Symmetry Elements II 3 D Symmetry We nowSymmetry Elements II 3 D Symmetry We now
Cnidarians By Lauren Lorenzo Body Symmetry Radial SymmetryCnidarians By Lauren Lorenzo Body Symmetry Radial Symmetry
The PlanarReflective Symmetry Transform Princeton University Motivation SymmetryThe PlanarReflective Symmetry Transform Princeton University Motivation Symmetry
Symmetry Elements Lecture 5 Symmetry Motif the fundamentalSymmetry Elements Lecture 5 Symmetry Motif the fundamental
Crystalline state Symmetry in nature Symmetry in artsCrystalline state Symmetry in nature Symmetry in arts