3 1 Solving Systems of Equations by Graphing

3. 1 Solving Systems of Equations by Graphing Goals: ~Solve systems of equations by graphing ~Determine whether a system is consistent and independent, consistent and dependent, or inconsistent

Terms n System of Equations: Two or more equations with the same variables l Consistent: Has at least 1 solution n n l Independent: Exactly one solution Dependent: Infinite number of solutions Inconsistent: No solution

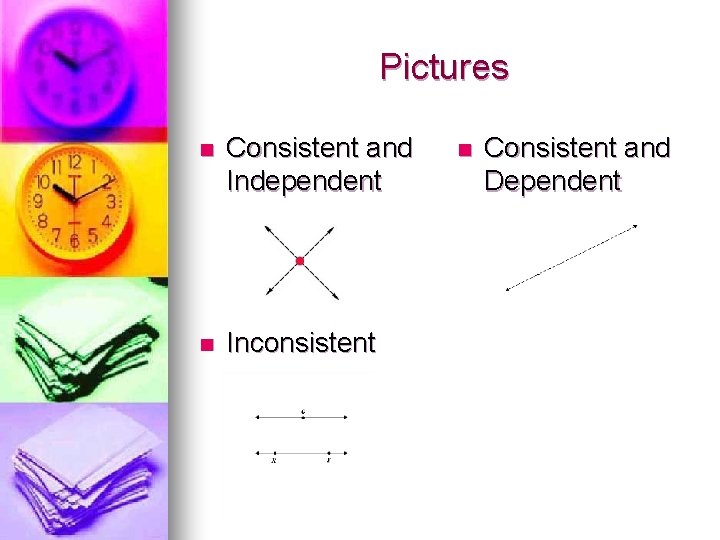
Pictures n Consistent and Independent n Inconsistent n Consistent and Dependent

Example 1: Solve by graphing n 2 x+y = 5 x–y=1 l Answer: Write each equation in slope-intercept form. n 2 x+y=5 --> y=-2 x+5 n x- y = 1 --> -y=-x+1 --> y=x-1 l Graph. (Graph y-int then follow the slope[rise/run] to get the next point) n The point where they cross is the solution

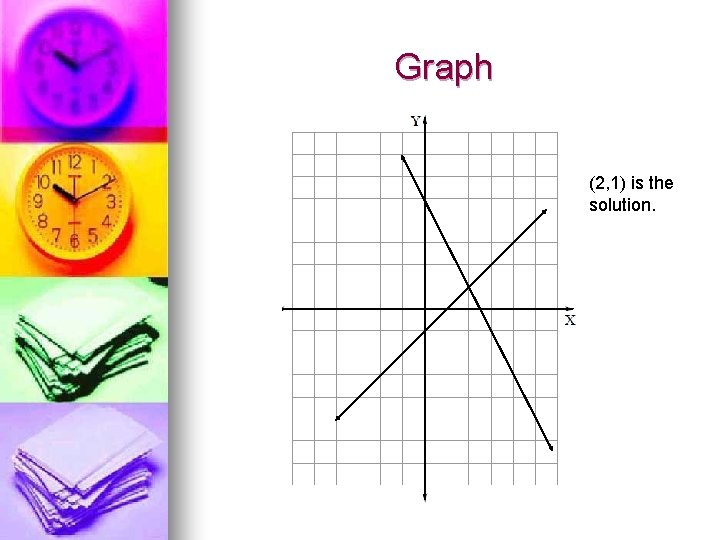
Graph (2, 1) is the solution.

Example 2: Solve by graphing and describe as consistent and independent, cons. and dependent, or inconsistent n

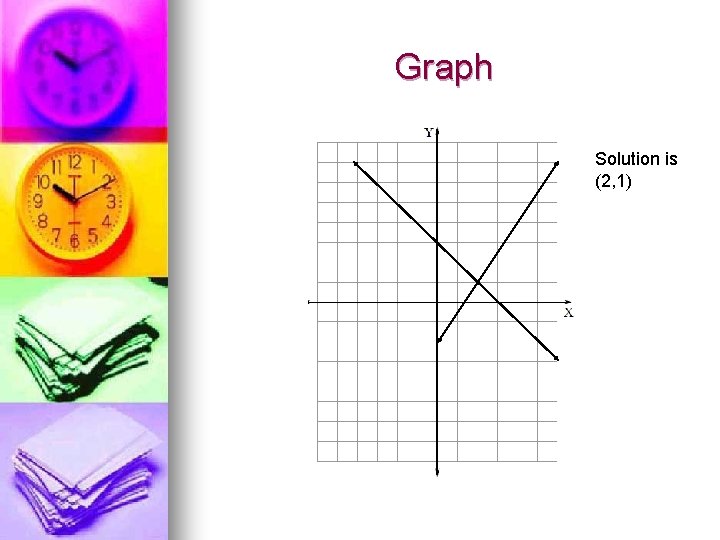
Graph Solution is (2, 1)

Answer: n They cross only once, so the graphs are consistent and independent

Example 2 a: Without graphing, describe as consistent and independent, cons. and dependent, or inconsistent n n n y = -x + 3 2 y = -2 x + 6 Solution : Put in slopeintercept form l Graph using y-int and slope l n n y = -x + 3

Answer n They both make the same graph, so they are consistent and dependent!!!

Without graphing, describe as consistent and independent, cons. and dependent, or inconsistent n 2 a. y = 3 x + 2 y = 3 x -5 n 2 b y = ½ x -6 y = 4 x + 10

Mr. Frazer bought 2 lbs of cheddar cheese and 3 lbs of turkey. He paid $26. 35. Mrs. Cooper paid $18. 35 for 1. 5 lbs of cheese and 2 lbs of turkey. What was the price per pound of each item? n