3 1 Numeration Systems Students will be able

3 -1 Numeration Systems Students will be able to understand explain • Numbers, their origin, and their representation in numerals and models. • Different numeration systems including the Hindu. Arabic system. • Place value and counting in base ten and other bases. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 1

Definition Numerals: written symbols to represent cardinal numbers. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 2

Numeration System Numeration system: a collection of properties and symbols agreed upon to represent numbers systematically. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 3

Tally Numeration System Uses single strokes (tally marks) to represent each object that is counted. = 13 ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 4

Egyptian Numeration System ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 5

Babylonian Numeration System ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 6

Mayan Numeration System ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 7

Roman Numeration System ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 8

Roman Numeration System ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 9

Hindu-Arabic Numeration System 1. All numerals are constructed from the 10 digits — 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. 2. Place value is based on powers of 10, the number base of the system. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 10

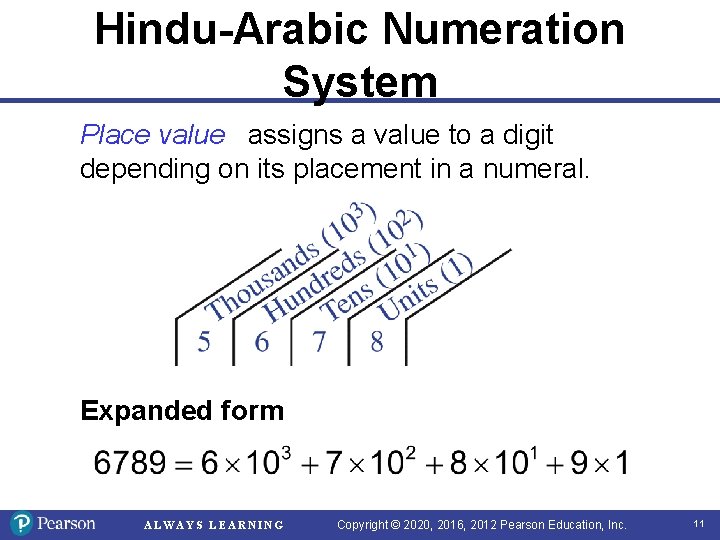
Hindu-Arabic Numeration System Place value assigns a value to a digit depending on its placement in a numeral. Expanded form ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 11

Definition of an If a is any number and n is any natural number, then n factors If a ≠ 0, then a 0 = 1. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 12

Base-ten blocks 1 long → 101 = 1 row of 10 units 1 flat → 102 = 1 row of 10 longs, or 100 units 1 block→ 103 = 1 row of 10 flats, or 100 longs, or 1000 units ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 13

Example 1 Trade 1 flats, 17 longs, and 16 units to obtain the fewest blocks possible. 11 flats 17 longs 1 long 18 longs ALWAYS LEARNING 16 units (16 units = 1 long 6 units and 6 units) 6 units (after the first trade) Copyright © 2020, 2016, 2012 Pearson Education, Inc. 14

Example 1 (continued) 11 flats 1 flat 12 flats 18 longs 6 units (18 longs = 1 flat and 8 longs 6 units (after the second trade) (12 flats = 1 block and 2 flats) 12 flats 8 longs 6 units 1 block 2 flats 8 longs 6 units As a result of the trading, we obtain 1 block, 2 flats, 8 longs, and 6 units. This trade yields the fewest number of pieces, 1 + 2 + 8 + 6 = 17 ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 15

Other Number Base Systems Quinary (basefive) system ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 16

Example 3 Convert 11244 five to base 10. 54 = 625 1 53 = 125 1 ALWAYS LEARNING 52 = 25 2 51 = 5 4 50 = 1 4 Copyright © 2020, 2016, 2012 Pearson Education, Inc. 17

Base Two Binary system – only two digits Base two is especially important because of its use in computers. One of the two digits is represented by the presence of an electrical signal and the other by the absence of an electrical signal. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 18

Example 4 a Convert 10111 two to base ten. 24 = 16 1 23 = 8 0 ALWAYS LEARNING 22 = 4 1 21 = 2 1 20 = 1 1 Copyright © 2020, 2016, 2012 Pearson Education, Inc. 19

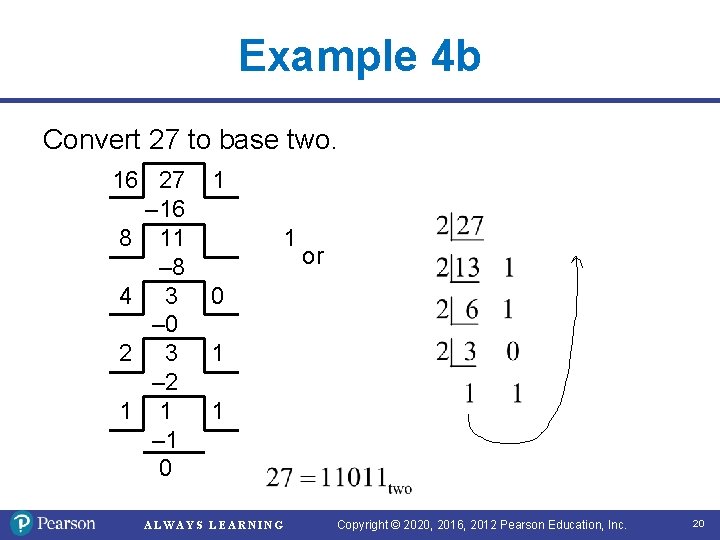
Example 4 b Convert 27 to base two. 16 27 – 16 8 11 – 8 4 3 – 0 2 3 – 2 1 1 – 1 0 1 1 or 0 1 1 ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 20

Base Twelve Duodecimal system – twelve digits Use T to represent a group of 10. Use E to represent a group of 11. The base-twelve digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, T, and E. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 21

Example 5 a Convert E 2 Ttwelve to base ten. ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 22

Example 5 b Convert 1277 to base twelve. 144 1277 – 1152 12 125 – 120 1 5 – 5 0 ALWAYS LEARNING 8 T 5 1277 ten = 8 T 5 twelve Copyright © 2020, 2016, 2012 Pearson Education, Inc. 23

Example 6 Rob used base twelve to write the following: g 36 twelve = 1050 ten What is the value of g? ALWAYS LEARNING Copyright © 2020, 2016, 2012 Pearson Education, Inc. 24