3 1 Lines and Angles StandardObjectives Identify relationships

3. 1 Lines and Angles

Standard/Objectives: • Identify relationships between lines. • Identify angles formed by transversals.

Definitions • Parallel lines – Two lines are parallel lines if they are coplanar and do not intersect. • Skew lines—Lines that do not intersect and are not coplanar. • Parallel planes—two planes that do not intersect.

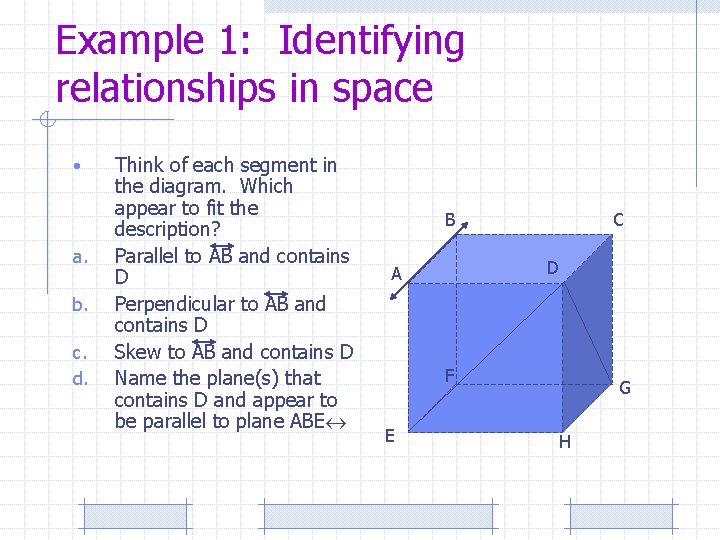
Example 1: Identifying relationships in space • a. b. c. d. Think of each segment in the diagram. Which appear to fit the description? Parallel to AB and contains D Perpendicular to AB and contains D Skew to AB and contains D Name the plane(s) that contains D and appear to be parallel to plane ABE B C D A F E G H

Solution CD, GH and EF are all parallel to AB, but only CD passes through D and is parallel to AB. b. BC, AD, AE and BF are all perpendicular to AB, but only AD passes through D and is perpendicular to AB c. DG, DH, and DE all pass through D and are skew to AB. d. Only plane DCH contains D and is parallel to plane ABE a.

Postulate 13: Parallel Postulate • If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line. P l

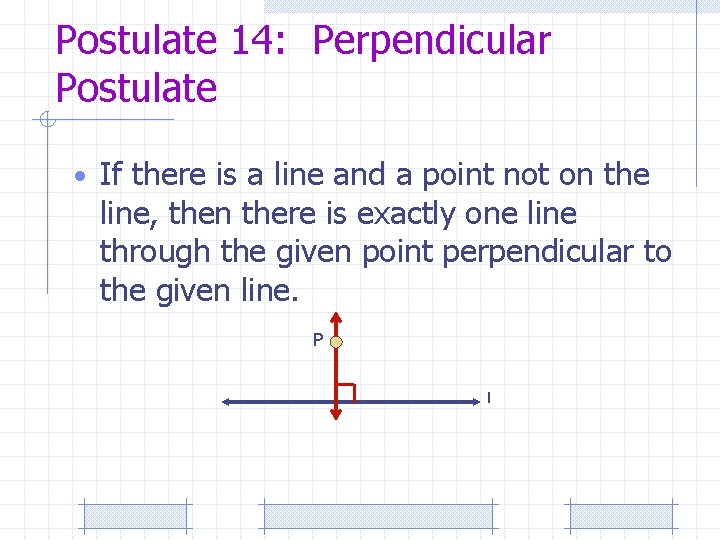
Postulate 14: Perpendicular Postulate • If there is a line and a point not on the line, then there is exactly one line through the given point perpendicular to the given line. P l

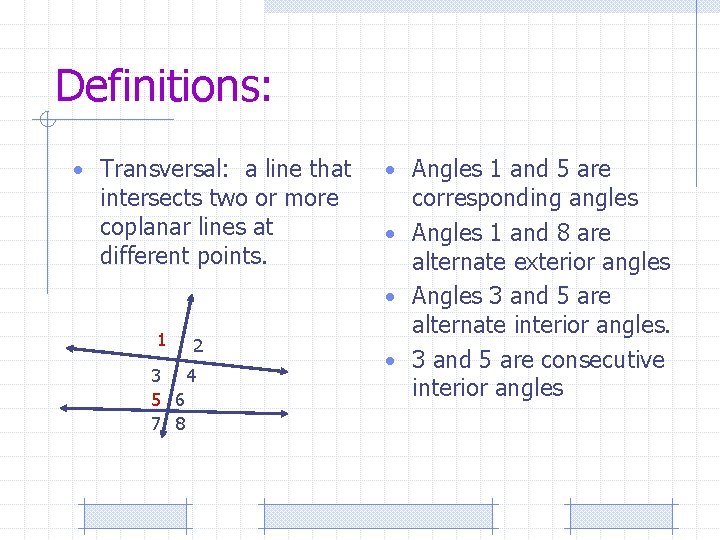
Definitions: • Transversal: a line that intersects two or more coplanar lines at different points. 1 2 3 4 5 6 7 8 • Angles 1 and 5 are corresponding angles • Angles 1 and 8 are alternate exterior angles • Angles 3 and 5 are alternate interior angles. • 3 and 5 are consecutive interior angles

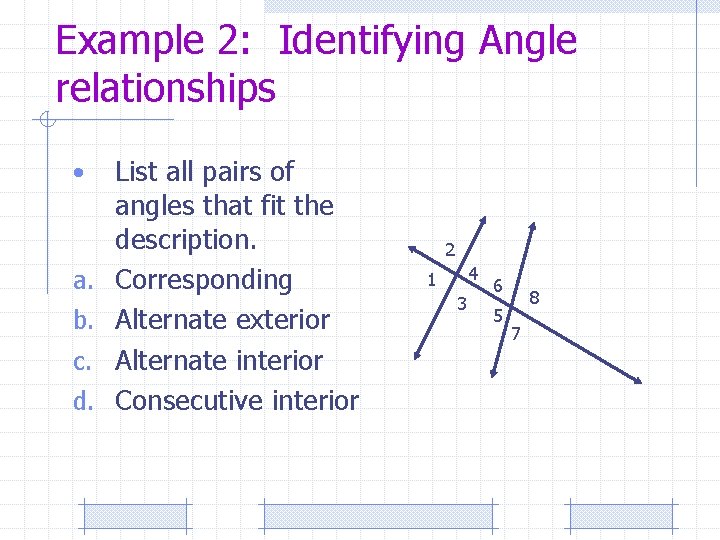
Example 2: Identifying Angle relationships • a. b. c. d. List all pairs of angles that fit the description. Corresponding Alternate exterior Alternate interior Consecutive interior 2 4 1 3 6 5 8 7

Solution: a. 1 and 5; 2 and 6; 3 and 7, 4 b. 1 c. 3 d. 3 and and 8 8, 2 and 7 6, 4 and 5 5, 4 and 6