3 1 CHAPTER Activity Cost Behavior 3 2

3 -1 CHAPTER Activity Cost Behavior

3 -2 Objectives 1. Define cost behavior fixed, After studying this variable, and mixed costs. chapter, you should 2. Explain the role be of the usage model ableresource to: in understanding cost behavior. 3. Separate mixed costs into their fixed and variable components using the high-low method, the scatterplot method, and the method of least squares. continued

3 -3 Objectives 4. Evaluate the reliability of a cost equation. 5. Discuss the role of multiple regression in assessing cost behavior. 6. Describe the use of managerial judgment in determining cost behavior.

3 -4 Fixed Costs A cost that stays the same as output changes is a fixed cost.

3 -5 Fixed Costs Cutting machines are leased for $60, 000 per year and have the capacity to produce up to 240, 000 units a year.

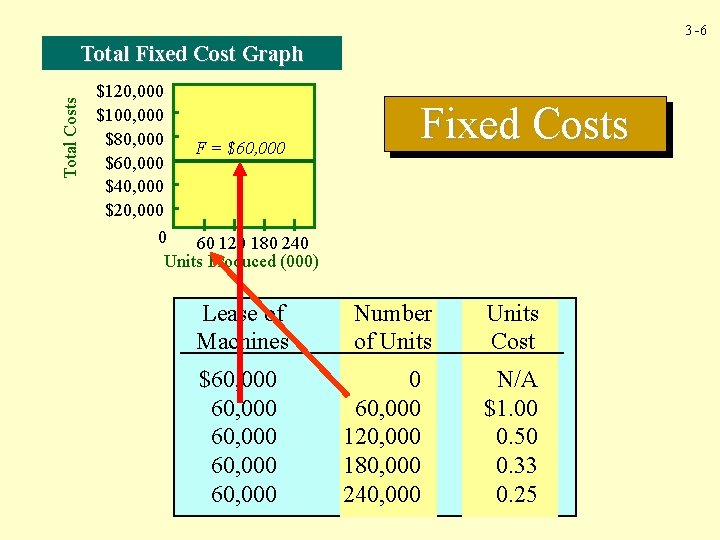
3 -6 Total Costs Total Fixed Cost Graph $120, 000 $100, 000 $80, 000 F = $60, 000 $40, 000 $20, 000 0 60 120 180 240 Units Produced (000) Lease of Machines $60, 000 60, 000 Fixed Costs Number of Units 0 60, 000 120, 000 180, 000 240, 000 Units Cost N/A $1. 00 0. 50 0. 33 0. 25

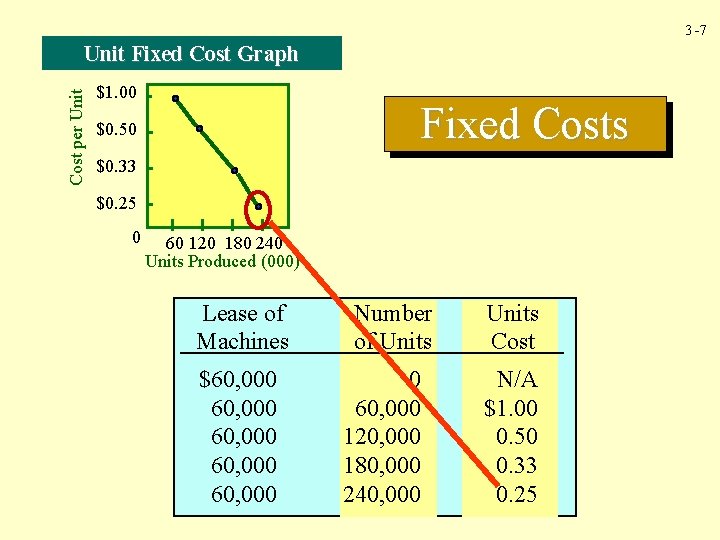
3 -7 Cost per Unit Fixed Cost Graph $1. 00 Fixed Costs $0. 50 $0. 33 $0. 25 0 60 120 180 240 Units Produced (000) Lease of Machines $60, 000 60, 000 Number of Units 0 60, 000 120, 000 180, 000 240, 000 Units Cost N/A $1. 00 0. 50 0. 33 0. 25

3 -8 A variable cost is a cost that, in total, varies in direct proportion to changes in output. Variable Cost

Variable Cost As the cutting machines cut each unit, they use 0. 1 kilowatt-hour at $2. 00 per kilowatt hour. Thus, the cost of each unit is $0. 20 ($2 x 0. 1). 3 -9

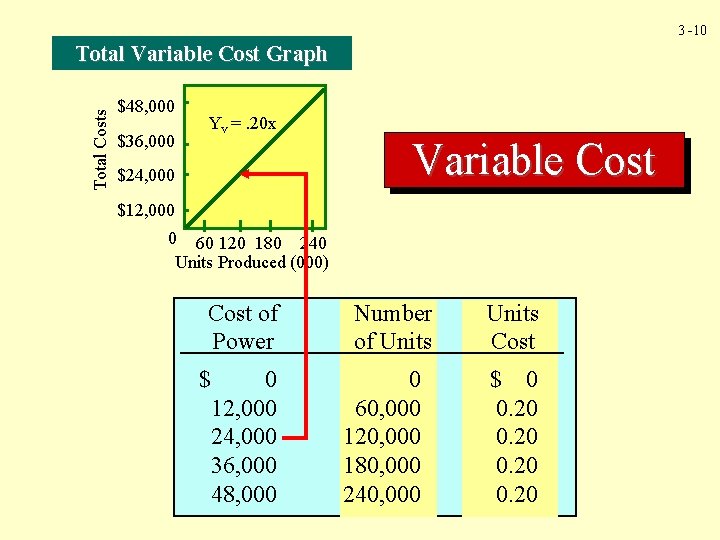
3 -10 Total Costs Total Variable Cost Graph $48, 000 $36, 000 Yv =. 20 x $24, 000 Variable Cost $12, 000 0 60 120 180 240 Units Produced (000) Cost of Power $ 0 12, 000 24, 000 36, 000 48, 000 Number of Units 0 60, 000 120, 000 180, 000 240, 000 Units Cost $ 0 0. 20

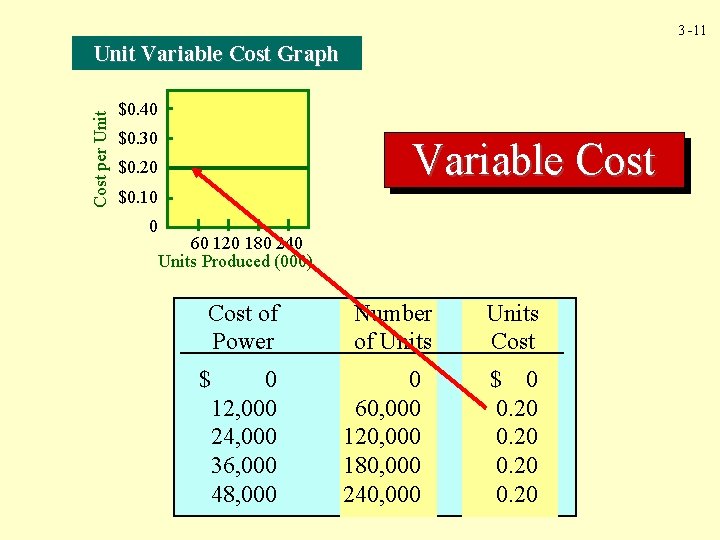
3 -11 Cost per Unit Variable Cost Graph $0. 40 $0. 30 Variable Cost $0. 20 $0. 10 0 60 120 180 240 Units Produced (000) Cost of Power $ 0 12, 000 24, 000 36, 000 48, 000 Number of Units 0 60, 000 120, 000 180, 000 240, 000 Units Cost $ 0 0. 20

3 -12 A mixed cost is a cost that has both a fixed and a variable component.

3 -13 Sales representatives often are paid a salary plus a commission on sales.

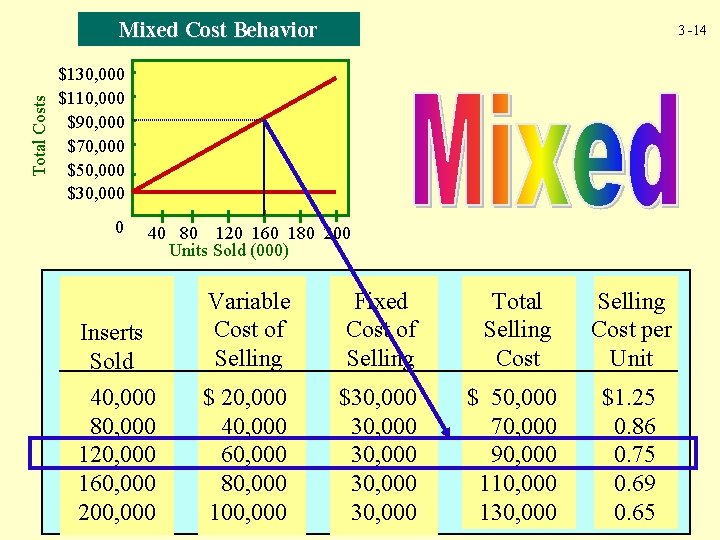
Total Costs Mixed Cost Behavior 3 -14 $130, 000 $110, 000 $90, 000 $70, 000 $50, 000 $30, 000 0 40 80 120 160 180 200 Units Sold (000) Inserts Sold 40, 000 80, 000 120, 000 160, 000 200, 000 Variable Cost of Selling Fixed Cost of Selling Total Selling Cost per Unit $ 20, 000 40, 000 60, 000 80, 000 100, 000 $30, 000 30, 000 $ 50, 000 70, 000 90, 000 110, 000 130, 000 $1. 25 0. 86 0. 75 0. 69 0. 65

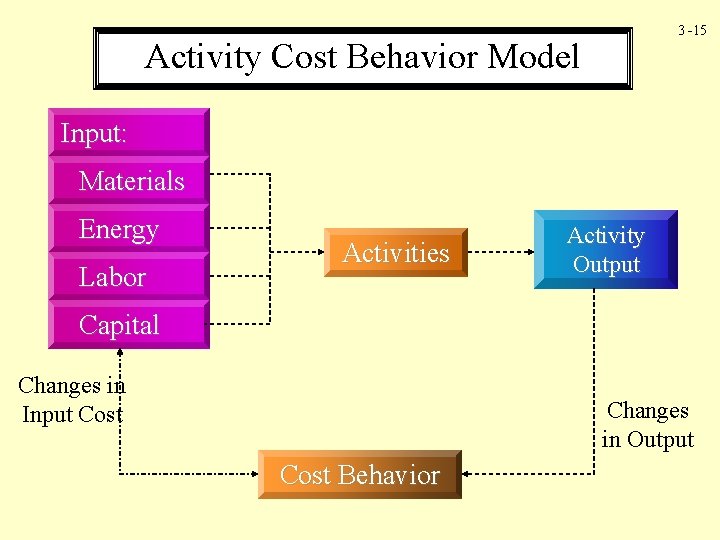
3 -15 Activity Cost Behavior Model Input: Materials Energy Labor Activities Activity Output Capital Changes in Input Cost Changes in Output Cost Behavior

3 -16 Flexible resources are resources acquired as used and needed. Materials and energy are examples.

3 -17 Committed resources are supplied in advance of usage. Buying or leasing a building is an example of this form of advance resource acquisition.

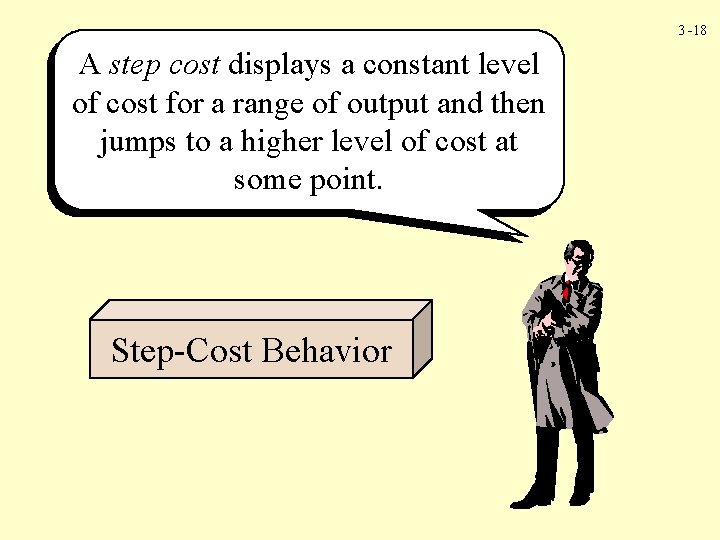
3 -18 A step cost displays a constant level of cost for a range of output and then jumps to a higher level of cost at some point. Step-Cost Behavior

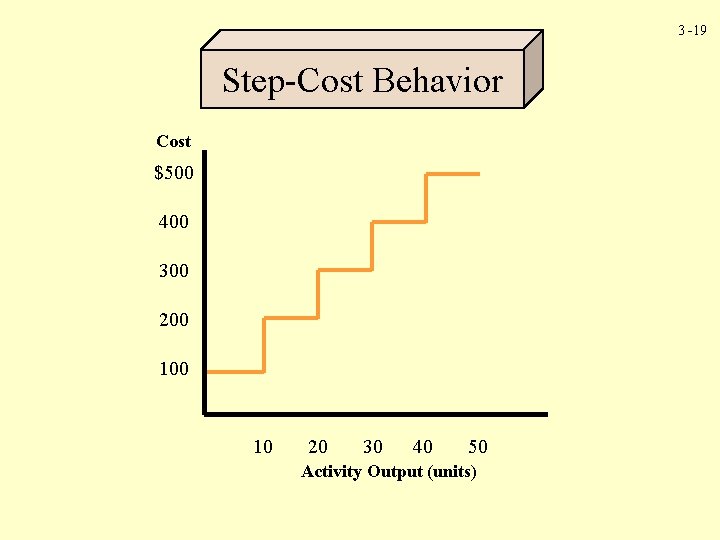
3 -19 Step-Cost Behavior Cost $500 400 300 200 10 20 30 40 50 Activity Output (units)

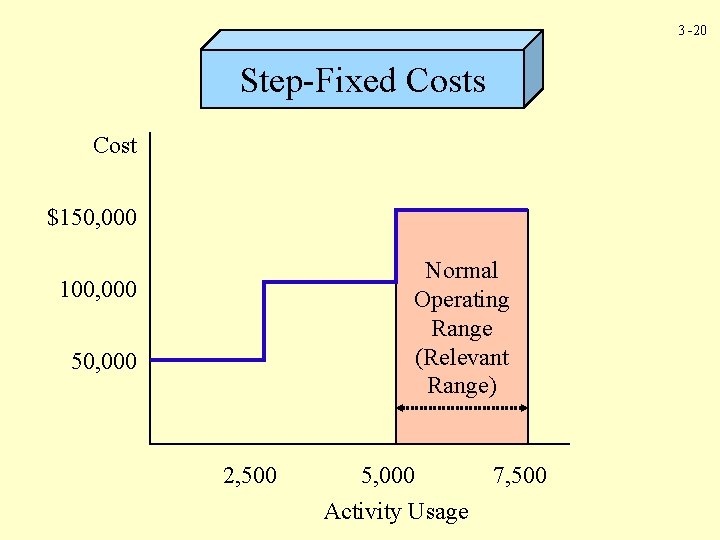
3 -20 Step-Fixed Costs Cost $150, 000 Normal Operating Range (Relevant Range) 100, 000 50, 000 2, 500 5, 000 Activity Usage 7, 500

3 -21 Step-Cost Behavior ü Three engineers hired at $50, 000 each ü Each engineer is capable of processing 2, 500 change orders ü $90, 000 was spent on supplies for the engineering activity ü There were 6, 000 orders processed ü The company could process as many as 7, 500 orders

3 -22 Step-Cost Behavior Available orders = Orders used + Orders unused 7, 500 orders = 6, 000 orders + 1, 500 orders Fixed engineering rate = $150, 000/7, 500 = $20 per change order Variable engineering rate = $90, 000/6, 000 = $15 per change order

3 -23 Step-Cost Behavior The relationship between resources supplied and resources used is expressed by the following equation: Resources available = Resources used + Unused capacity

3 -24 Step-Cost Behavior Cost of orders supplied = Cost of orders used + Cost of unused orders = [($20 + $15) x 6, 000] + ($20 x 1, 500) = $240, 000 The $30, 000 of excess engineering capacity means that a new product could be Equal to the $150, 000 spent on introducedengineers without and increasing current the $90, 000 spending on engineering. spent on supplies.

3 -25 Methods for Separating Mixed Costs The High-Low Method The Scatterplot Method The Method of Least Squares Variable Component Fixed Component

3 -26 The linearity assumption assumes that variable costs increase in direct proportion to the number of units produced (or activity units used).

3 -27 Methods for Separating Mixed Costs Y = a + bx Total Fixed Number of Total Cost Variable Cost. Units per Unit

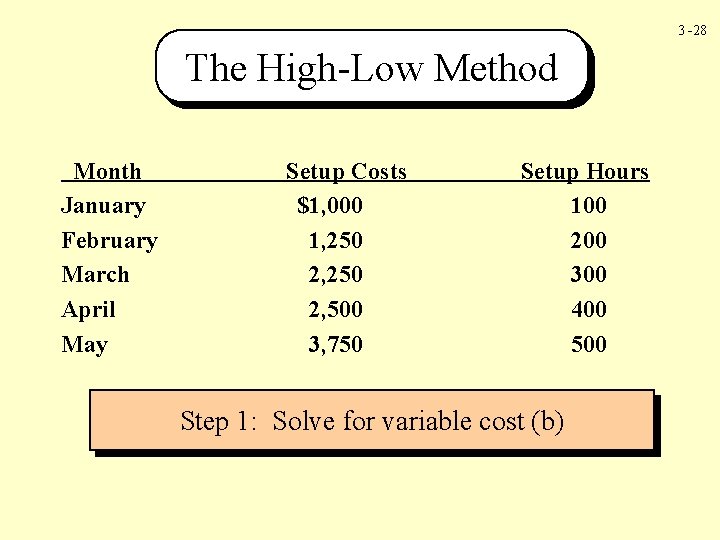
3 -28 The High-Low Method Month January February March April May Setup Costs $1, 000 1, 250 2, 500 3, 750 Setup Hours 100 200 300 400 500 Step 1: Solve for variable cost (b)

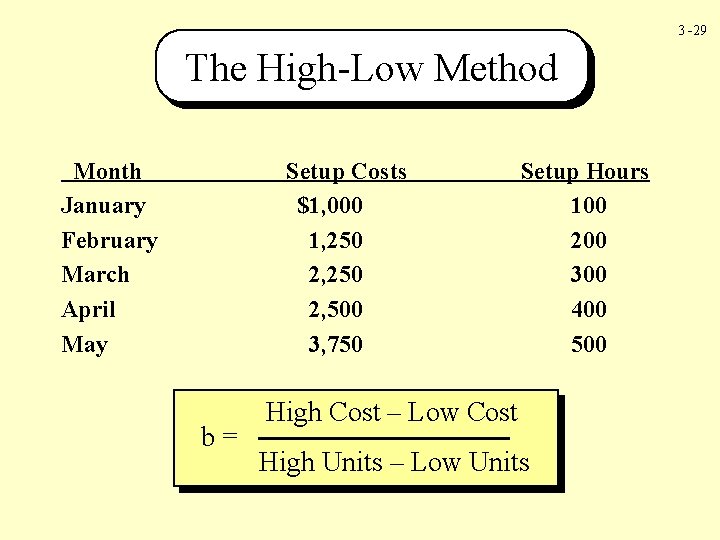
3 -29 The High-Low Method Month January February March April May Setup Costs $1, 000 1, 250 2, 500 3, 750 b= Setup Hours 100 200 300 400 500 High Cost – Low Cost High Units – Low Units

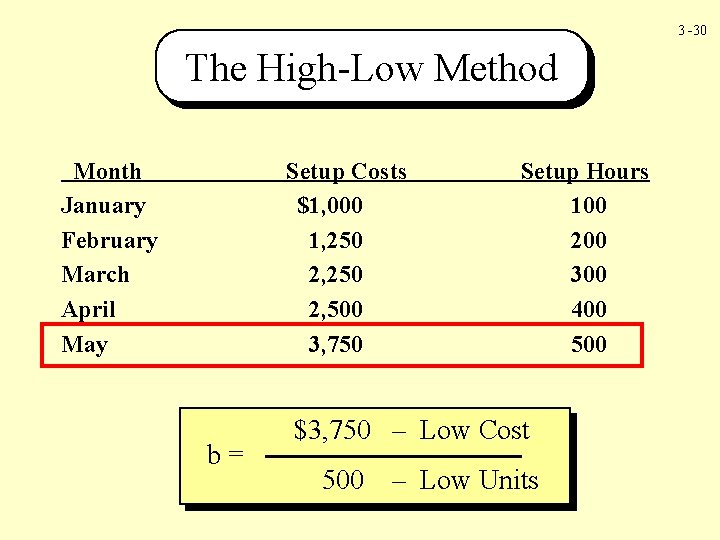
3 -30 The High-Low Method Month January February March April May Setup Costs $1, 000 1, 250 2, 500 3, 750 b= Setup Hours 100 200 300 400 500 High $3, 750 Cost – Low Cost High 500 Units –– Low Units

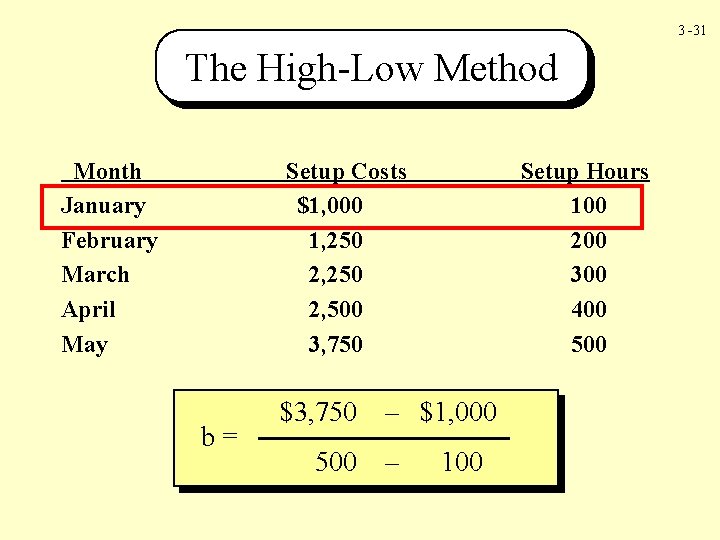
3 -31 The High-Low Method Month January February March April May Setup Costs $1, 000 1, 250 2, 500 3, 750 b= $3, 750 500 Setup Hours 100 200 300 400 500 – Low $1, 000 Cost – Low 100 Units

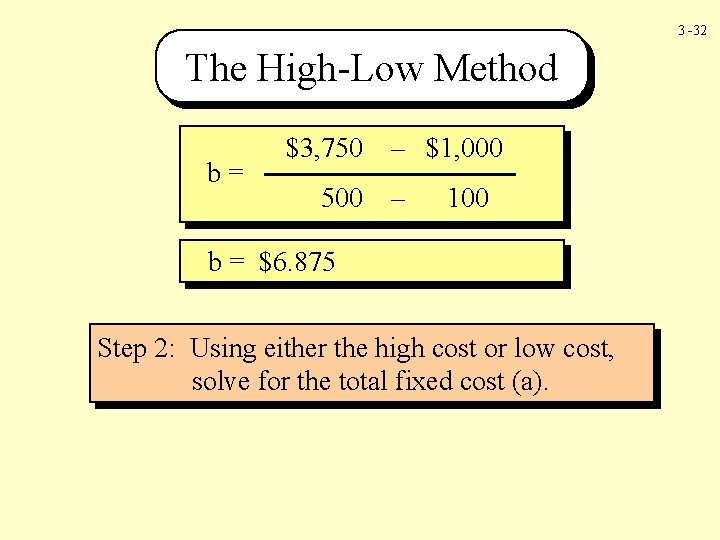
3 -32 The High-Low Method b= $3, 750 500 – $1, 000 – 100 b = $6. 875 Step 2: Using either the high cost or low cost, solve for the total fixed cost (a).

3 -33 The High-Low Method Y = $3, 750 = $312. 50 = a + b (x) a + $6. 875(500) a High End Y = $1, 000 = $312. 50 = a + b (x) a + $6. 875(100) a Low End The cost formula using the high-low method is: Total cost = $312. 50 + ($6. 875 x Setup hours)

3 -34 The Scatterplot Method

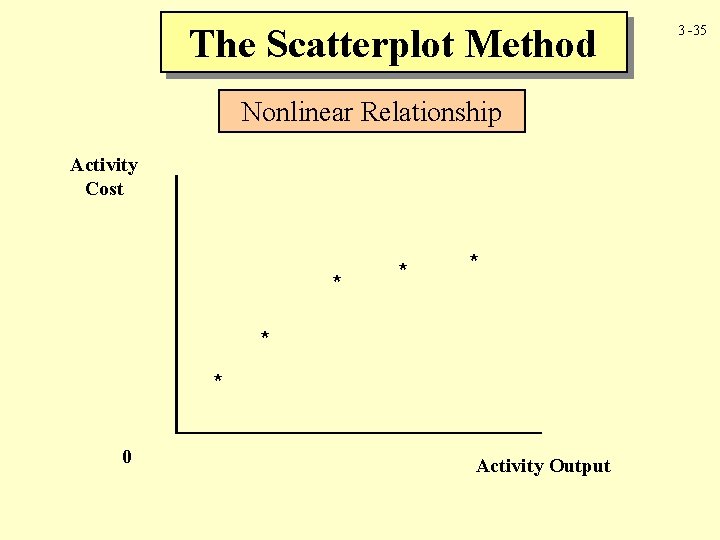
The Scatterplot Method Nonlinear Relationship Activity Cost * * * 0 Activity Output 3 -35

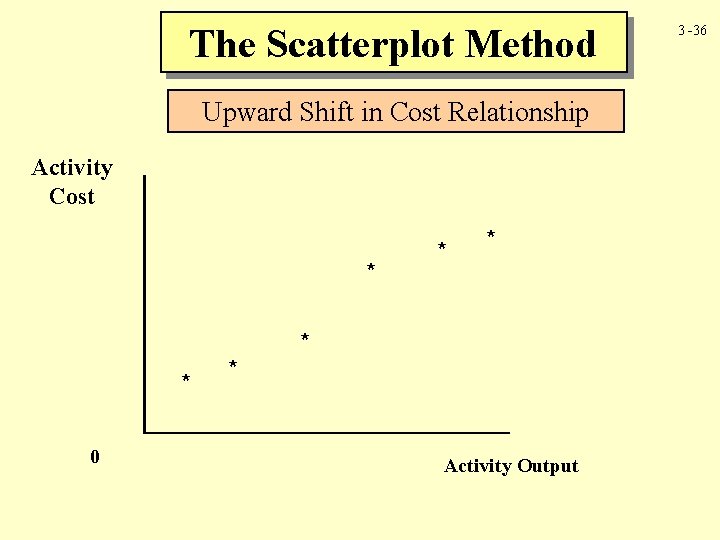
The Scatterplot Method Upward Shift in Cost Relationship Activity Cost * * * 0 * Activity Output 3 -36

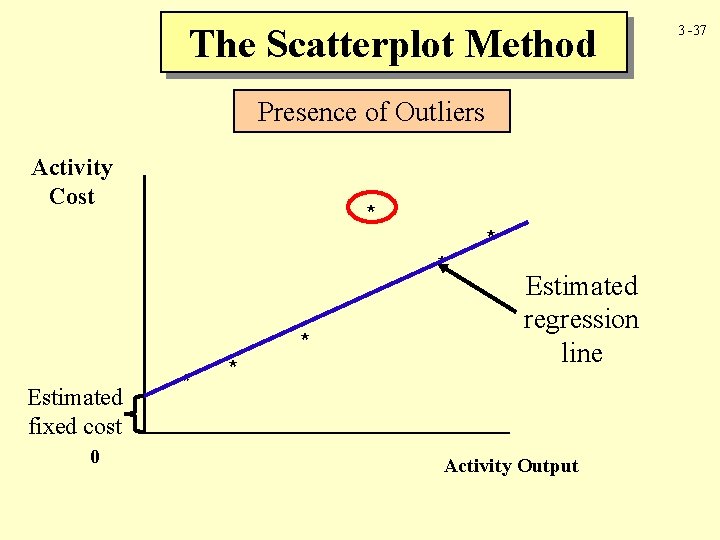
The Scatterplot Method Presence of Outliers Activity Cost * * * Estimated fixed cost 0 * * * Estimated regression line Activity Output 3 -37

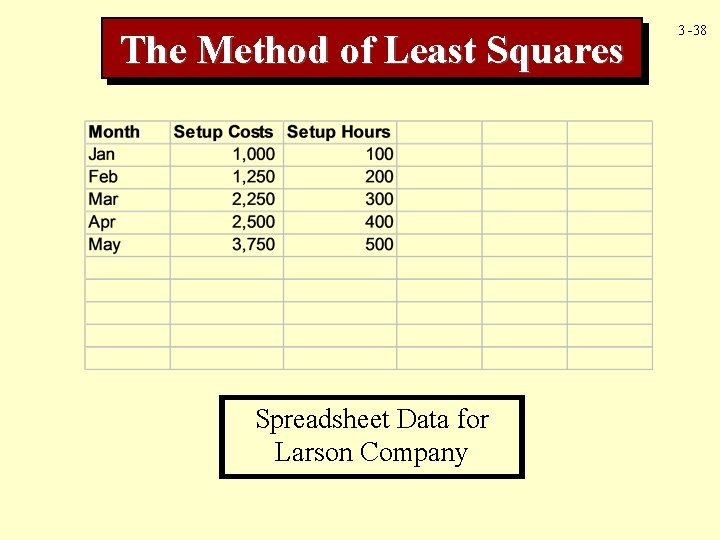
The Method of Least Squares Spreadsheet Data for Larson Company 3 -38

The Method of Least Squares Regression Output for Larson Company 3 -39

The Method of Least Squares The results give rise to the following equation: Setup costs = $125 + ($6. 75 x Setup hours) R 2 =. 944, or 94. 4 percent of the variation in setup costs is explained by the number of setup hours variable. 3 -40

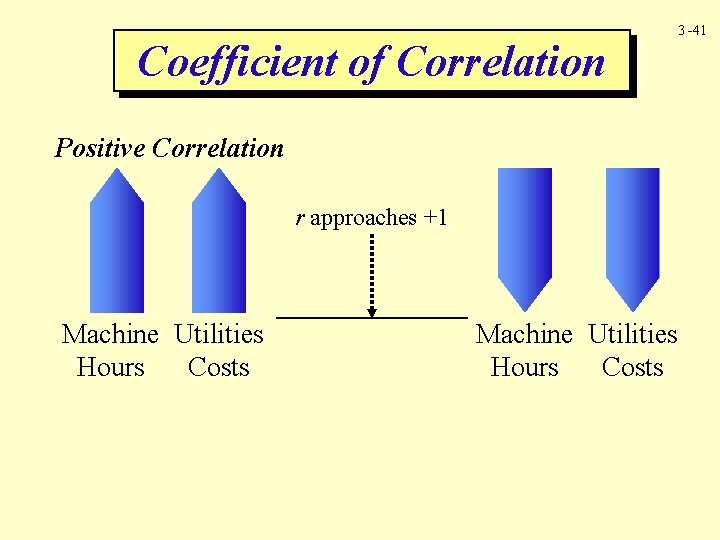
Coefficient of Correlation 3 -41 Positive Correlation r approaches +1 Machine Utilities Hours Costs

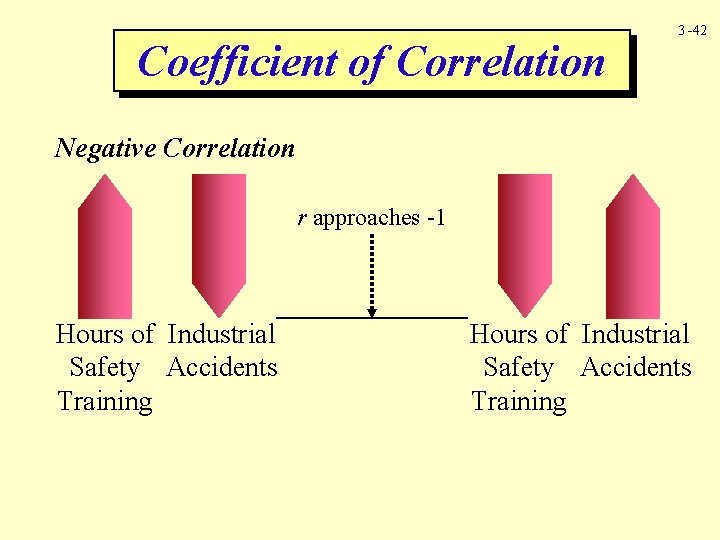
Coefficient of Correlation 3 -42 Negative Correlation r approaches -1 Hours of Industrial Safety Accidents Training

Coefficient of Correlation 3 -43 No Correlation r~0 Hair Accounting Length Grade

3 -44 Multiple Regression TC = b 0 + ( b 1 X 1) + (b 2 X 2) +. . . b 0 = the fixed cost or intercept b 1 = the variable rate for the first independent variable X 1 = the first independent variable b 2 = the variable rate for the second independent variable X 2 = the second independent variable

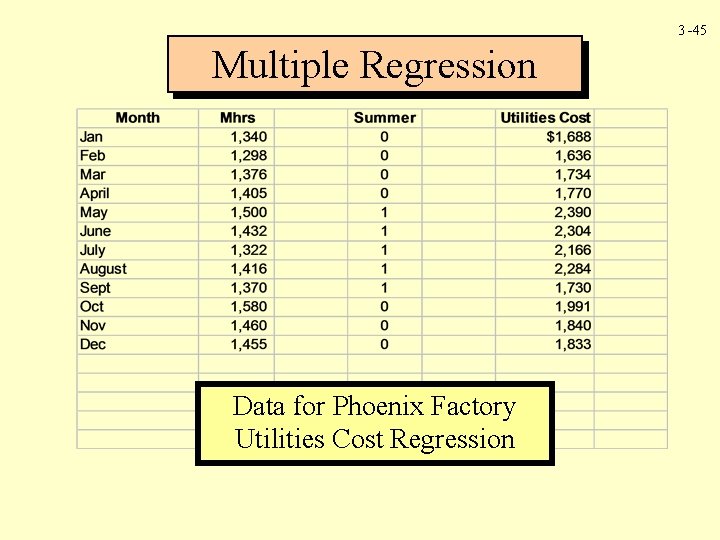
3 -45 Multiple Regression Data for Phoenix Factory Utilities Cost Regression

3 -46 Multiple Regression for Phoenix Factory Utilities Cost

3 -47 Multiple Regression The results gives rise to the following equation: Utilities cost = $243. 11 + $1. 097(Machine hours) + ($510. 49 x Summer) R 2 =. 967, or 96. 7 percent of the variation in utilities cost is explained by the machine hours and summer variables.

3 -48 Managerial Judgment Managerial judgment is critically important in determining cost behavior, and it is by far the most widely used method in practice.

3 -49 Chapter Three The End

3 -50