2s Complement Another system that lets us represent




















- Slides: 21

2’s Complement • • Another system that lets us represent negative numbers MSB is STILL the sign bit, but there is no negative zero Negative numbers count backwards and wrap around Calculating 2’s complement (Pos Neg) 1. Flip the bits ( 0 1 and 1 0 ) 2. Add 1

Example ( Pos Neg ) 110 00012 -110 11112 1. Flip bits: 1110 2. Add 1: 1110 +0001 1111

Another Example ( Pos Neg ) 2510 000110012 -2510 11100111 2 1. Flip bits: 11100110 2. Add 1: 11100110 +00000001 11100111

Your Turn • Assuming an 8 -bit restriction, what is -2110 in 2’s complement? 1. Flip bits 2. Add 1 Answer: 111010112

Your Turn • Assuming an 8 -bit restriction, what is -3010 in 2’s complement? 1. Flip bits 2. Add 1 Answer: 111000102

Example ( Neg Pos ) -410 11002 410 01002 1. Flip bits: 0011 2. Add 1: 0011 +0001 0100

Another Example ( Neg Pos ) -2910 111000112 2910 000111012 1. Flip bits: 00011100 2. Add 1: 00011100 +000000011101

Your Turn • Assuming 2’s complement, what is the decimal value of 111110012? 1. Flip bits 2. Add 1 Answer: -710

Your Turn • Assuming 2’s complement, what is the decimal value of 111010102? 1. Flip bits 2. Add 1 Answer: 22

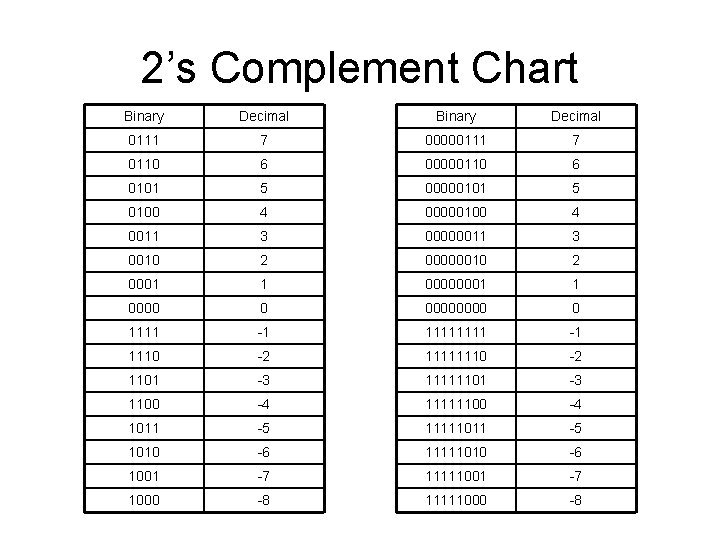
2’s Complement Chart Binary Decimal 0111 7 00000111 7 0110 6 00000110 6 0101 5 00000101 5 0100 4 00000100 4 0011 3 00000011 3 0010 2 00000010 2 0001 1 0000 0 1111 -1 1110 -2 11111110 -2 1101 -3 11111101 -3 1100 -4 11111100 -4 1011 -5 11111011 -5 1010 -6 11111010 -6 1001 -7 11111001 -7 1000 -8 11111000 -8

SHORTCUT! 1. Find the 1 on the farthest right 2. Flip all the bits to the left of the 1 (DO NOT FLIP THE 1) Example: 4210 001010102 -4210 110101102

Awesomeness of 2’s Complement • No more negative zero • Lower minimum value: -(2 N-1) • So what’s the big deal? – Everything is addition – No need for special hardware to do subtraction

2’s Complement Addition • Just like normal positive binary addition • You MUST restrict the number of bits • IGNORE any overflow bits – maintain bit-size restriction

Positive Addition Example 1210 + 410 = 1610 Assuming 2’s complement 000010102 +000000102 000011002 1210 + 410 1610

Negative Addition Example -1210 + -410 = -1610 111101002 +111111002 111100002 NOTE: -1210 + -410 -1610 We ignored the last overflow bit on the left!

Your Turn • Show the binary addition of -14 + -3 = -17

Subtraction Example 1610 – 410 = 1610 + -410 = 1210 000100002 +111111002 000011002 NOTE: We ignored the last overflow bit on the left!

Your Turn • Show the binary subtraction of 23 – 10 = 13

Overflow / Underflow Problem • Addition and bit-size restriction allow for possible overflow / underflow • Overflow – when the addition of two binary numbers yields a result that is greater than the maximum possible value • Underflow – when the addition/subtraction of two binary numbers yields a result that is less than the minimum possible value

Overflow Example • Assume 4 -bit restriction and 2’s complement • Maximum possible value: 24 -1 – 1 = 7 610 + 310 = 910 01102 +00112 10012 610 +310 -710 not good!

Underflow Example • Assume 4 -bit restriction and 2’s complement • Minimum possible value: -(24 -1) = -8 -510 + -510 = -1010 10112 +10112 01102 -510 +-510 610 not good!