290 N The Unknown Component Problem Lecture 24

290 N: The Unknown Component Problem Lecture 24 FSM Decomposition using Partitions on States

Outline Ø Ø Ø Ø Once upon a time… Motivating example Terminology Definition of SP-partitions Decomposition using SP-partitions Computation of SP-partitions Extensions for ND FSMs

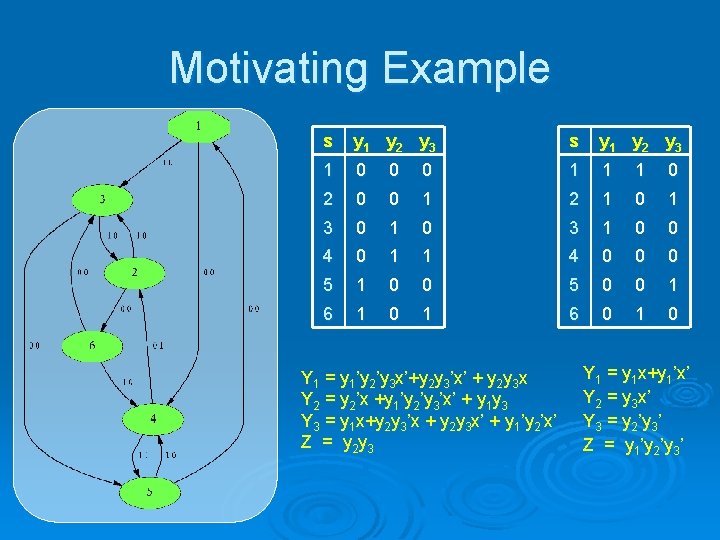
Motivating Example s y 1 y 2 y 3 1 0 0 0 1 1 1 0 2 0 0 1 2 1 0 1 3 0 1 0 3 1 0 0 4 0 1 1 4 0 0 0 5 1 0 0 5 0 0 1 6 1 0 1 6 0 1 0 Y 1 = y 1’y 2’y 3 x’+y 2 y 3’x’ + y 2 y 3 x Y 2 = y 2’x +y 1’y 2’y 3’x’ + y 1 y 3 Y 3 = y 1 x+y 2 y 3’x + y 2 y 3 x’ + y 1’y 2’x’ Z = y 2 y 3 Y 1 = y 1 x+y 1’x’ Y 2 = y 3 x’ Y 3 = y 2’y 3’ Z = y 1’y 2’y 3’

Terminology FSM is {I, O, S, , } Ø A partition on S is a set of disjoint subsets of states, whose set-union is S, i. e. Ø = {Bk}; Bi Bj = , i j; Ui Bi = S Ø Notations l l l Subsets Bk are called blocks B (s) denotes the block containing state s s t iff s and t are in the same block, i. e. B (s) = B (t)

Partitions and Equivalence Relations Ø Relation R on sets S and T is a subset of pairs l Ø Equivalence relation R l l l Ø R = { (s, t) | s R t } Reflexive: for all s, s R s Symmetric: if s R t, then t R s Transitive: if s R t and t R u, then s R u Proposition. If R is an equivalence relation on S, then the set of equivalence classes is a partition on S, and conversely, every partition on S is an equivalence relation R

Operations on Partitions Ø Definition. Product of partitions, 1 and 2, is a partition 1 2 on S such that s 1 2 t iff s 1 t and s 2 t Ø Definition. Sum of partitions, 1 and 2, is a partition 1+ 2 on S such that s 1+ 2 t iff there exist a sequence of states in S, s=s 0, s 1, …, sn, for which si 1 si+1 or si 2 si+1 Ø Definition. Partition 2 is larger or equal to partition 1, 1 2, if and only if 1 2 = 1 (equivalently, 1 + 2 = 2)

Partitions as a Lattice Ø Definition. Let (S, ) be a partially ordered set, and T be a subset of S. Then s S is the least upper bound (l. u. b. ) of T iff l s t for all t in T l s’ t for all t in T implies that s’ s Definition. A lattice is partially ordered set, L = (S, ), which has a l. u. b. and a g. l. b. Ø Definition. If L is a finite lattice, then it has a l. u. b. and g. l. b. for the set of all elements in L, denoted by 1 and 0. Element 1 is called identity, and 0 is called zero. Ø Theorem. Partitions form a lattice. Ø

Example Ø Lattice of subsets of S={1, 2, 3} Ø Lattice of partitions on S={1, 2, 3} {1, 2} {1, 3} {1, 2, 3} {1, 2 | 3} {1} {2} {1, 3|2} {1 | 2, 3} {1 | 2 | 3}

SP-Partitions Ø Definition. A partition on the set of states S of the machine M = (S, I, O, , ) has the substitution property (is SP-partition) iff the states in any block, under all inputs, transit into another block, i. e. x [ s t ] [ (s, x) (t, x) ]

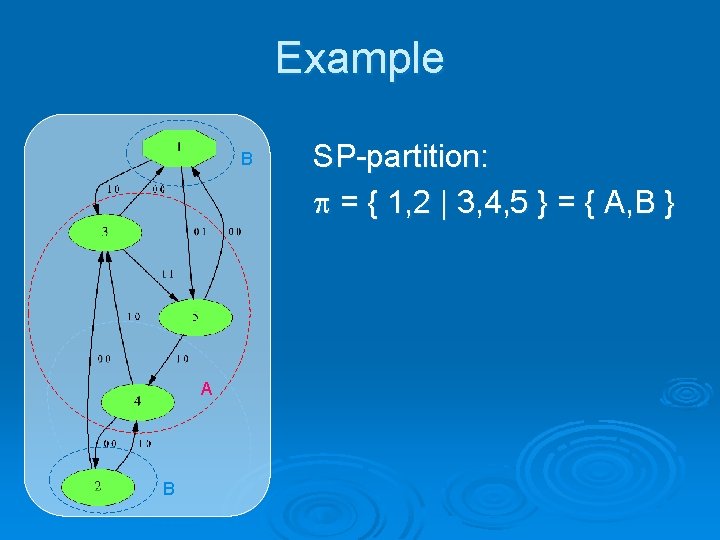
Example B A B SP-partition: = { 1, 2 | 3, 4, 5 } = { A, B }

-Image of FSM Ø Definition. Let be an SP-partition on the set of states S of the machine M = (S, I, O, , ). Then, the -image of M is the machine M = ({B }, I, ) with (B , x) = B ’ iff (B , x) B ’.

Example B A B SP-partition: = { 1, 2 | 3, 4, 5 } = { A, B }

Observations Observation 1. Machine M performs only part of the computation of machine M, because it only keeps track of which block of contains the given state. Ø Observation 2. If is an SP-partition, and we know the block of , which contains the given state of M, then we can compute the block of , to which this state of M is transformed by any input sequence. Machine M performs this computation. On the other hand, if is not an SP-partition, then it is not possible to predict where the given state will go under some input sequences. In other words, an SP-partition defines an uncertainty about the states of M, which does not spread as the machine operates. Ø

SP-Partitions as a Sub-Lattice Ø Lemma. SP-partitions are closed under product and sum operations. Ø Theorem. SP-partitions form a sub-lattice of the lattice of all partitions

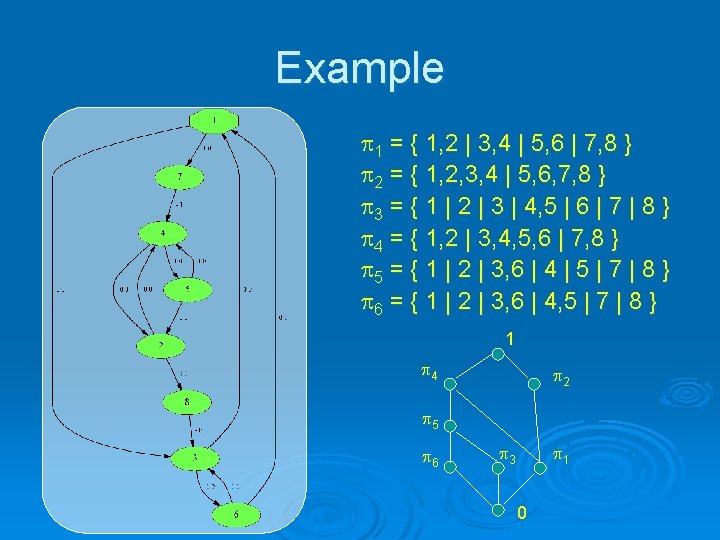
Observations Ø Lattice of SP-partitions shows all non-trivial parallel-serial decompositions of the FSM l Ø The lattice is a picture of FSM structure Algebraic properties of the lattice are reflected in the machine properties, and vice versa l FSMs can be classified according to their lattices

Decomposition of FSMs Definition. Machine M is decomposable into two machines, M 1 and M 2, if the set of i/o strings produced by M is equal to the set of i/o strings produced by the composition of M 1 and M 2. Ø Definition. Decomposition of M into two machines, M 1 and M 2, is non-trivial if M 1 and M 2 have fewer states than M. Ø

Parallel Composition Ø Definition. Given the state machines M 1 = (S 1, I, 1) and M 2 = (S 2, I, 2), and the output function : S 1 S 2 I O, the parallel composition of M 1 and M 2 is the machine M = (S 1 S 2, I, O, , ), where ((s 1, s 2), (x 1, x 2)) = ( 1(s 1, x 1), 2(s 2, x 2)). M I 1 M 2 S 1 O S 2

Serial Composition Ø Definition. Given the state machines M 1 = (S 1, I 1, 1) and M 2 = (S 2, I 2, 2) with I 2 = S 1 I 1, a set of output symbols O, and an output function : S 1 S 2 I 1 O, then the serial composition of M 1 and M 2 with the output function is the machine M = (S 1 S 2, I 1, O, , ), where ((s, t), x) = ( 1(s, x), 2(t, (s, x))). I 1 M M 1 S 1 M 2 S 2 O

Theory Ø Theorem 1. Machine M has a non-trivial parallel decomposition iff there exist two non-trivial SP-partitions 1 and 2 on the states of M, such that 1 2 = 0. Ø Theorem 2. Machine M has a non-trivial serial decomposition iff there exist a nontrivial SP-partition on the states of M.

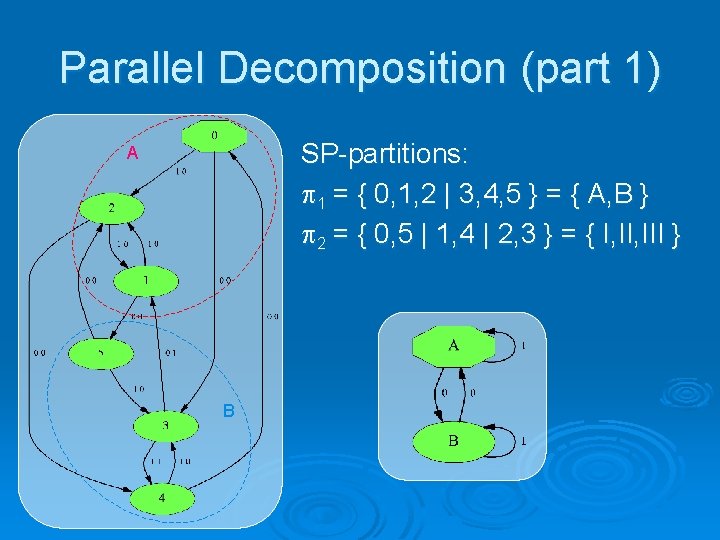
Parallel Decomposition (part 1) SP-partitions: 1 = { 0, 1, 2 | 3, 4, 5 } = { A, B } 2 = { 0, 5 | 1, 4 | 2, 3 } = { I, III } A B

Parallel Decomposition (part 2) M M 1 I M 2 M 1 M S 1 S 2 M 2

Serial Decomposition (part 1) B A B SP-partition: = { 1, 2 | 3, 4, 5 } = { A, B }

Serial Decomposition (part 2) a c b Another partition: = { 1, 3 | 2, 4 | 5 } = { a, b, c }

Serial Decomposition (part 3) M M M 1 M 2

Computation of All SP-partitions Ø For every pair of states, s and t, compute the SP -partition containing these states in one block. l Ø The resulting non-trivial partitions are the smallest partitions of the lattice of SP-partitions Find all possible sums of the above partitions l The resulting non-trivial partitions are the remaining partitions of the lattice of SP-partitions