28 December 2021 Compound angle identities LO To

28 December 2021 Compound angle identities LO: To derive and use the double angle identities. www. mathssupport. org

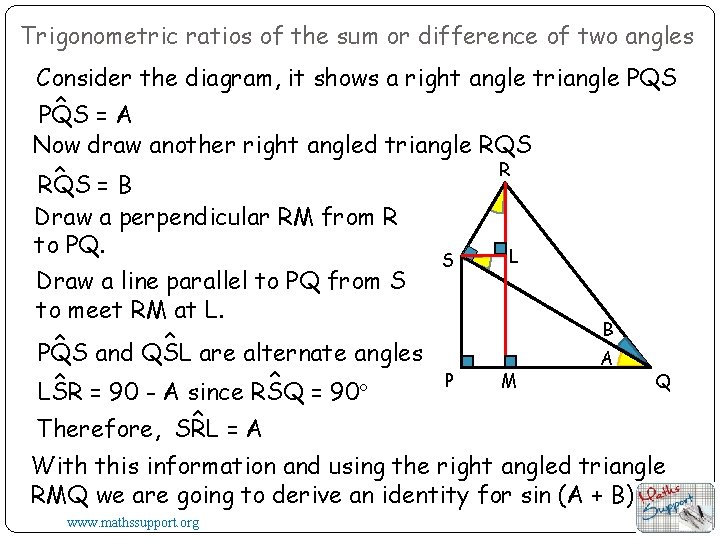
Trigonometric ratios of the sum or difference of two angles Consider the diagram, it shows a right angle triangle PQS ^ =A PQS Now draw another right angled triangle RQS R ^ RQS = B Draw a perpendicular RM from R to PQ. Draw a line parallel to PQ from S to meet RM at L. ^ are alternate angles ^ and QSL PQS ^ = 90º ^ = 90 - A since RSQ LSR ^ =A Therefore, SRL S L B P M A Q With this information and using the right angled triangle RMQ we are going to derive an identity for sin (A + B) www. mathssupport. org

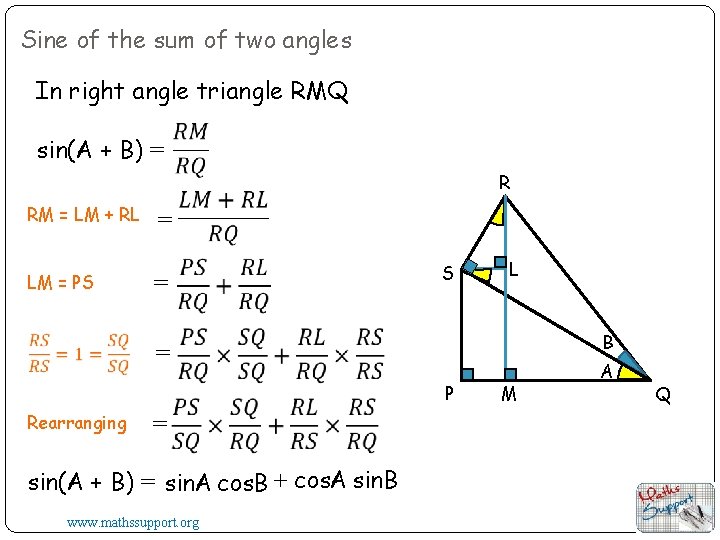
Sine of the sum of two angles In right angle triangle RMQ sin(A + B) = R RM = LM + RL LM = PS = = S L B = P Rearranging = sin(A + B) = sin. A cos. B + cos. A sin. B www. mathssupport. org M A Q

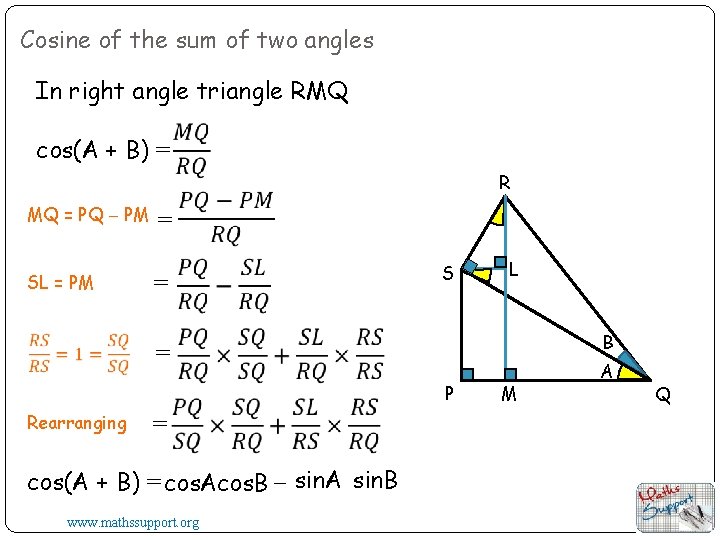
Cosine of the sum of two angles In right angle triangle RMQ cos(A + B) = R MQ = PQ PM SL = PM = = S L B = P Rearranging = cos(A + B) = cos. Acos. B sin. A sin. B www. mathssupport. org M A Q

Tangent of the sum of two angles We know the tangent identity tanq = tan(A + B) = Expand using the identities for the sine and cosine of the sum of two angles. Divide both the numerator and denominator by cos. Acos. B Simplify sin. A cos. B + cos. A sin. B cos. Acos. B = cos. Acos. B sin. A sin. B cos. Acos. B sin. A cos. B + cos. A sin. B = cos. Acos. B sin. A sin. B sin. A cos. B + cos. A sin. B cos. Acos. B = cos. Acos. B sin. A sin. B cos. Acos. B sin. A + sin. B cos. A cos. B = sin. A sin. B 1 cos. A cos. B tan(A + B) = www. mathssupport. org

Sine of the difference of two angles We already know that sin(A + B) = sin. A cos. B + cos. A sin. B To find sin(A B) we just consider the sum of a negative angle sin(A B) = Sin(A + ( B)) Using the identity for the sine of the sum of two angles sin(A + ( B)) = sin. A Cos( B) + cos. A Sin( B) We already know that cos( B) = cos. B sin( B) = sin. B Therefore sin(A B) = sin. A cos. B cos. A sin. B www. mathssupport. org

Cosine of the difference of two angles We already know that cos(A + B) = cos. Acos. B sin. A sin. B To find cos(A B) we just consider the sum of a negative angle cos(A B) = cos(A + ( B)) Using the identity for the cosine of the sum of two angles cos(A + ( B)) = cos. ACos( B) sin. A Sin( B) We already know that cos( B) = cos. B sin( B) = sin. B Therefore cos(A + B) = cos. Acos. B + sin. A sin. B www. mathssupport. org

Tangent of the difference of two angles We already know that tan(A + B) = To find tan(A B) we just consider the sum of a negative angle tan(A B) = tan(A + ( B)) Using the identity for the tangent of the sum of two angles tan. A + tan( B) tan(A + ( B)) = 1 tan. Atan( B) We already know that tan( B) = tan. B Therefore tan. A tan. B tan(A B) = 1 + tan. Atan. B www. mathssupport. org

Compound angle identities Show that sin(A + B) sin(A B) = sin 2 A sin 2 B Using the identities for the sum and difference of the sine of two angles. (sin. A cos. B + cos. A sin. B) (sin. A cos. B cos. A sin. B) Difference of two squares. sin 2 A cos 2 B cos 2 A sin 2 B Using the Pythagorean identity for cos 2 A sin 2 A cos 2 B sin 2 B (1 - sin 2 A) Expanding. sin 2 A cos 2 B sin 2 B + sin 2 Asin 2 B Reordering. sin 2 A cos 2 B + sin 2 Asin 2 B Common factor of the first two terms. sin 2 A (cos 2 B + sin 2 B) sin 2 B Using the Pythagorean identity. Therefore sin 2 A sin 2 B sin(A + B) sin(A B) = sin 2 A sin 2 B www. mathssupport. org

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org www. mathssupport. org