28 Alternating Current Circuits 1 2 3 4













- Slides: 34

28. Alternating Current Circuits 1. 2. 3. 4. 5. 6. Alternating Current Elements in AC Circuits LC Circuits Driven RLC Circuits & Resonance Power in AC Circuits Transformers & Power Supplies

Why does alternating current facilitate the transmission and distribution of electric power? EM induction allows voltage transformation.

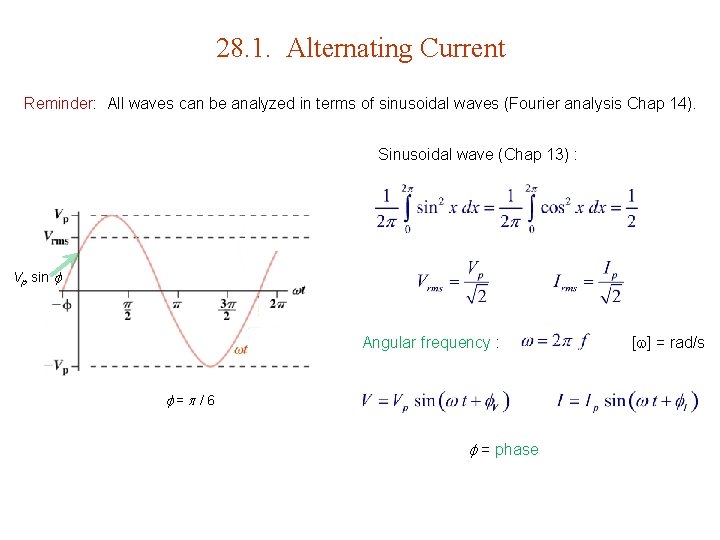
28. 1. Alternating Current Reminder: All waves can be analyzed in terms of sinusoidal waves (Fourier analysis Chap 14). Sinusoidal wave (Chap 13) : Vp sin Angular frequency : = /6 = phase [ ] = rad/s

Example 28. 1. Characterizing Household Voltage Standard household wiring supplies 110 V rms at 60 Hz. Express this mathematically, assuming the voltage is rising through 0 at t = 0.

28. 2. Current Elements in AC Circuits l Resistors l Capacitors l Inductors l Phasor Diagrams l Capacitors & Inductors: A Comparison

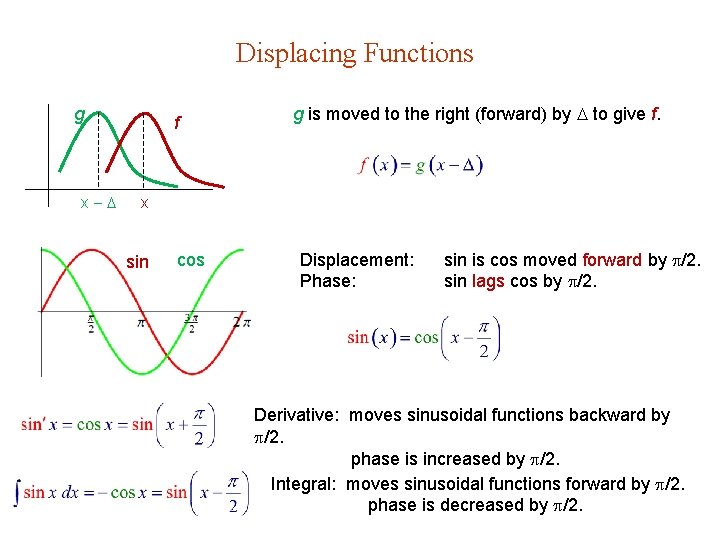
Displacing Functions g x f g is moved to the right (forward) by to give f. x sin cos Displacement: Phase: sin is cos moved forward by /2. sin lags cos by /2. Derivative: moves sinusoidal functions backward by /2. phase is increased by /2. Integral: moves sinusoidal functions forward by /2. phase is decreased by /2.

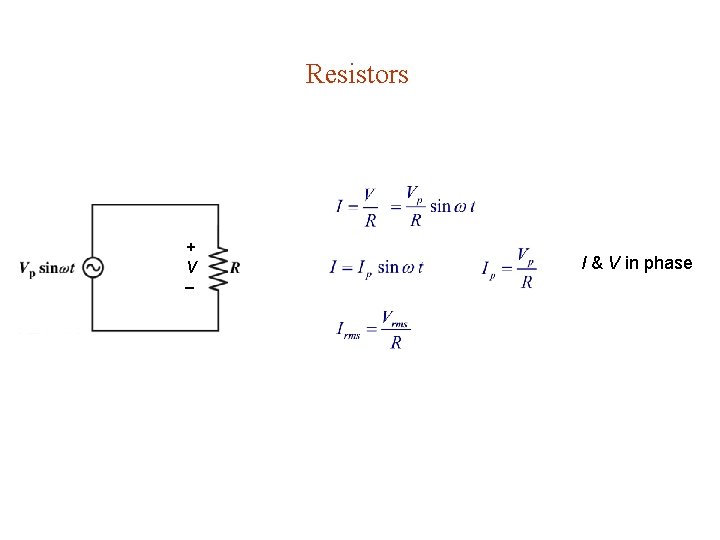
Resistors + V I & V in phase

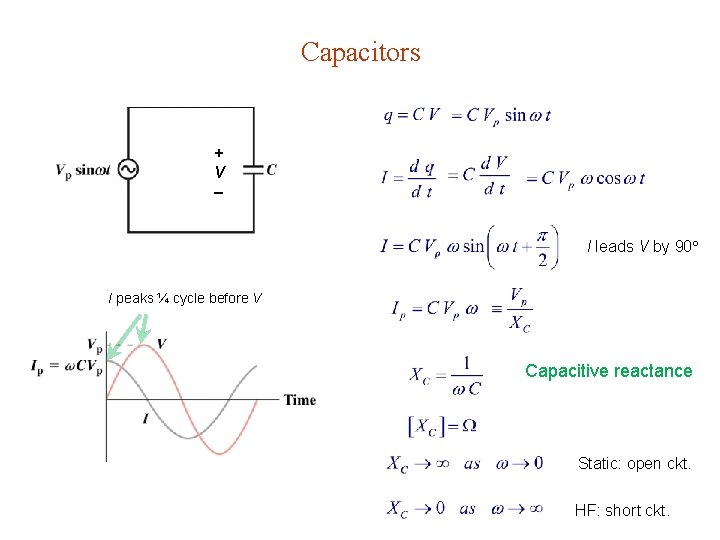
Capacitors + V I leads V by 90 I peaks ¼ cycle before V Capacitive reactance Static: open ckt. HF: short ckt.

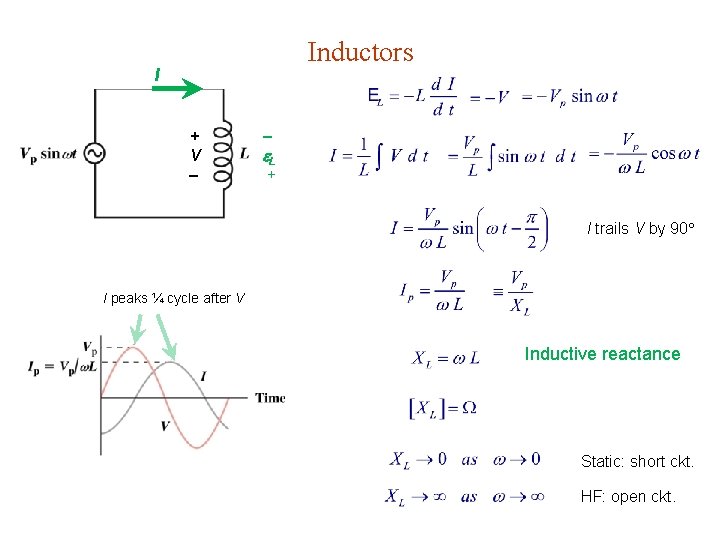
Inductors I + V L + I trails V by 90 I peaks ¼ cycle after V Inductive reactance Static: short ckt. HF: open ckt.

Table 28. 1. Amplitude & Phase in Circuit Elements Circuit Element Peak Current vs Voltage Phase Relation Resistor V & I in phase Capacitor V lags I 90 Inductor V leads I 90

GOT IT? 28. 1. A capacitor and an inductor are connected across separate but identical electric generators, and the same current flows in each. If the frequency of the generators is doubled, which will carry more current? Ans. is capacitor

Example 28. 2. Equal Currents? A capacitor is connected across a 60 -Hz, 120 -V rms power line, and an rms current of 200 m. A flows. (a) Find the capacitance. (b) What inductance, connected across the same powerline, would result in the same current? (c) How would the phases of the inductor & capacitor currents compare? (a) (b) (c) Capacitor: IC leads V by 90. Inductor: V leads IL by 90. IC leads IL by 180.

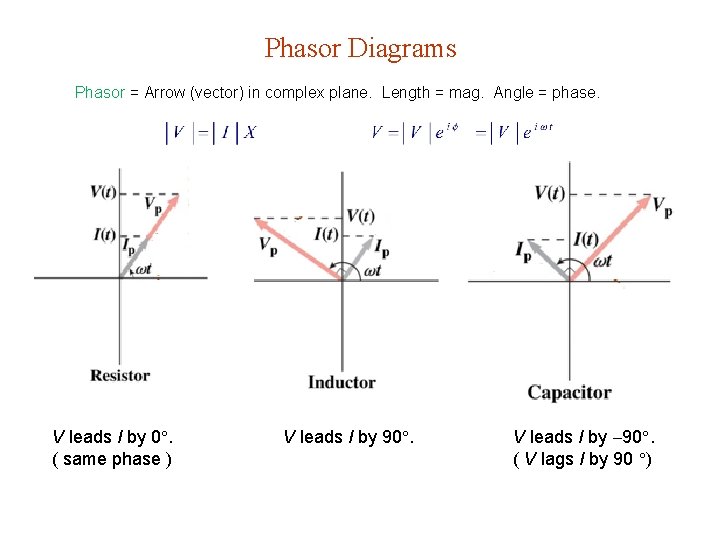
Phasor Diagrams Phasor = Arrow (vector) in complex plane. Length = mag. Angle = phase. V leads I by 0. ( same phase ) V leads I by 90. ( V lags I by 90 )

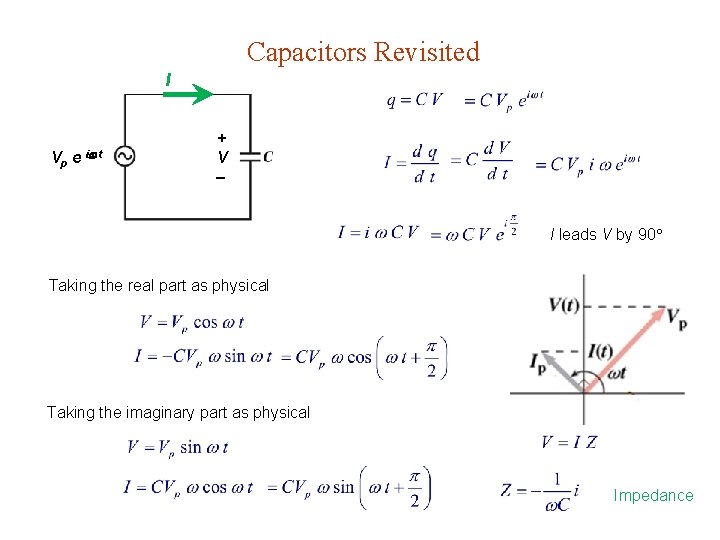
Capacitors Revisited I Vp e i t + V I leads V by 90 Taking the real part as physical Taking the imaginary part as physical Impedance

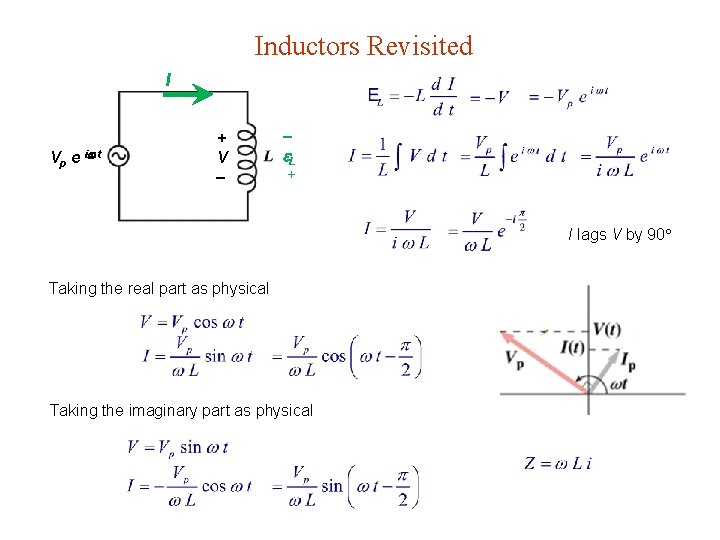
Inductors Revisited I Vp e i t + V L + I lags V by 90 Taking the real part as physical Taking the imaginary part as physical

Capacitors & Inductors: A Comparison C L translator: E B q B V I Z Y

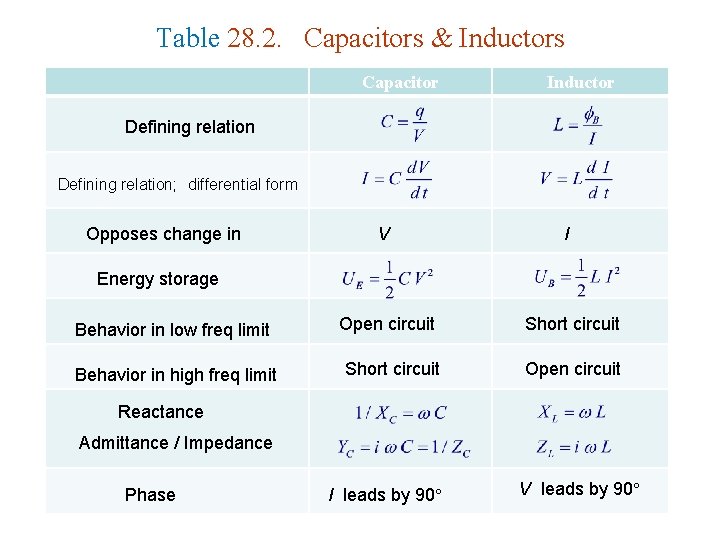
Table 28. 2. Capacitors & Inductors Capacitor Inductor Defining relation; differential form Opposes change in V I Energy storage Behavior in low freq limit Open circuit Short circuit Behavior in high freq limit Short circuit Open circuit Reactance Admittance / Impedance Phase I leads by 90 V leads by 90

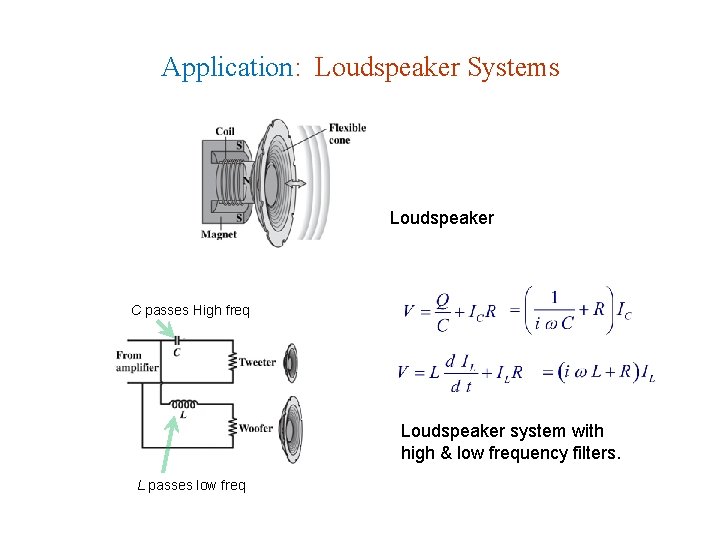
Application: Loudspeaker Systems Loudspeaker C passes High freq Loudspeaker system with high & low frequency filters. L passes low freq

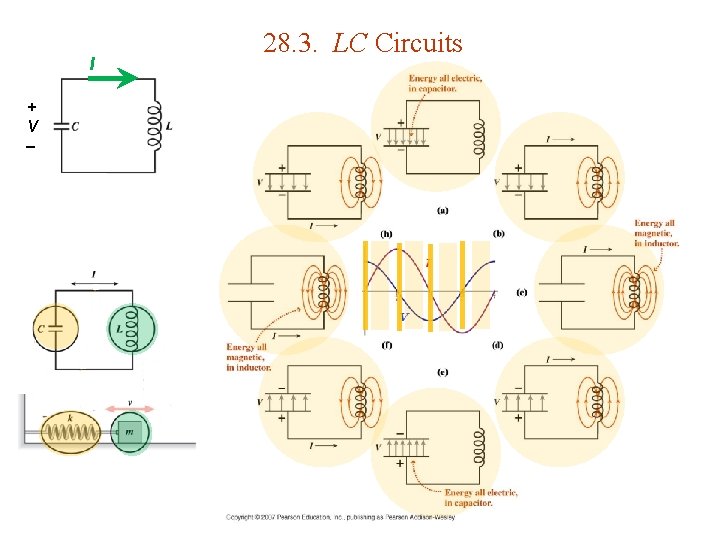
I + V 28. 3. LC Circuits

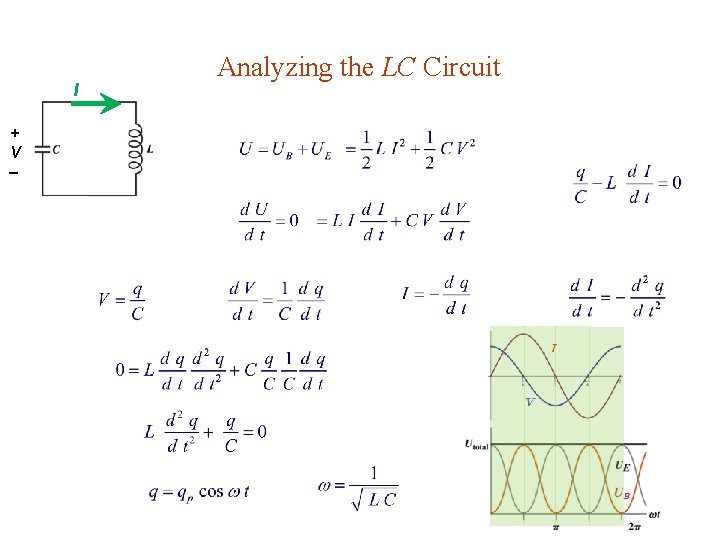
I + V Analyzing the LC Circuit

GOT IT? 28. 2 You have an LC circuit that oscillates at a typical AM radio frequency of 1 MHz. You want to change the capacitor so it oscillates at a typical FM frequency , 100 MHz. Should you make the capacitor (a) larger or (b) smaller ? By what factor ? 10 4

Example 28. 3. Tuning a Piano You wish to make an LC circuit oscillate at 440 Hz ( A above middle C ) to use in tuning pianos. You have a 20 -m. H inductor. (a) What value of capacitance should you use ? (b) If you charge the capacitor to 5. 0 V, what will be the peak current in the circuit ? (a) (b)

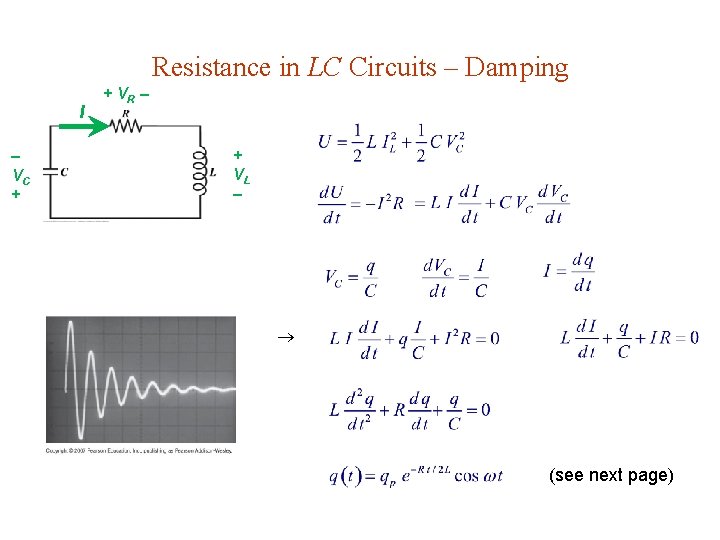
Resistance in LC Circuits – Damping I VC + + VR + VL (see next page)

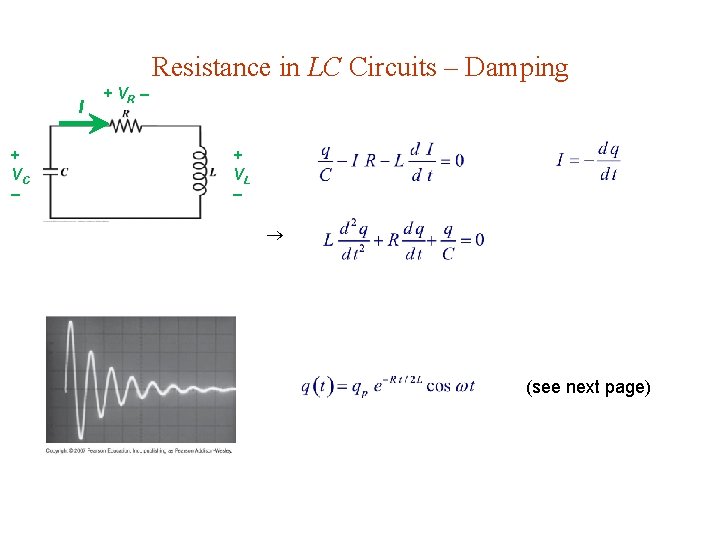
Resistance in LC Circuits – Damping I + VC + VR + VL (see next page)

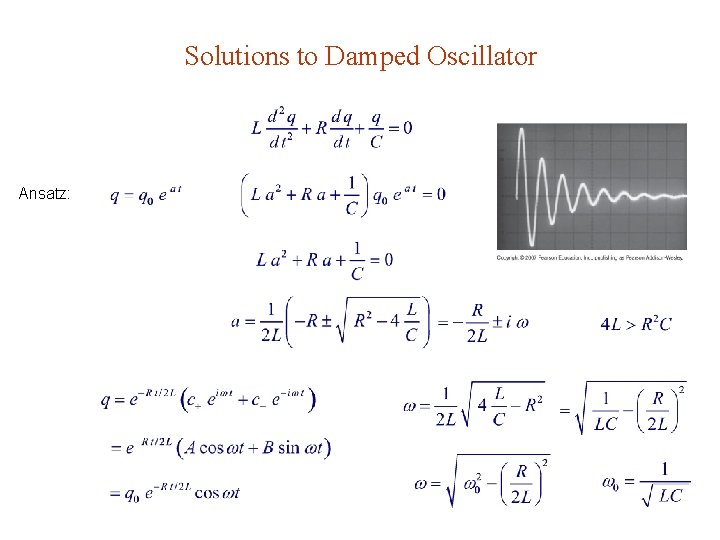
Solutions to Damped Oscillator Ansatz:

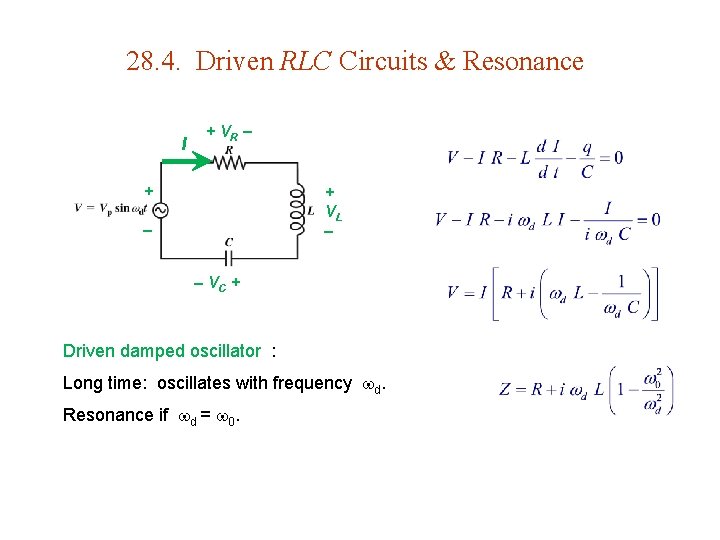
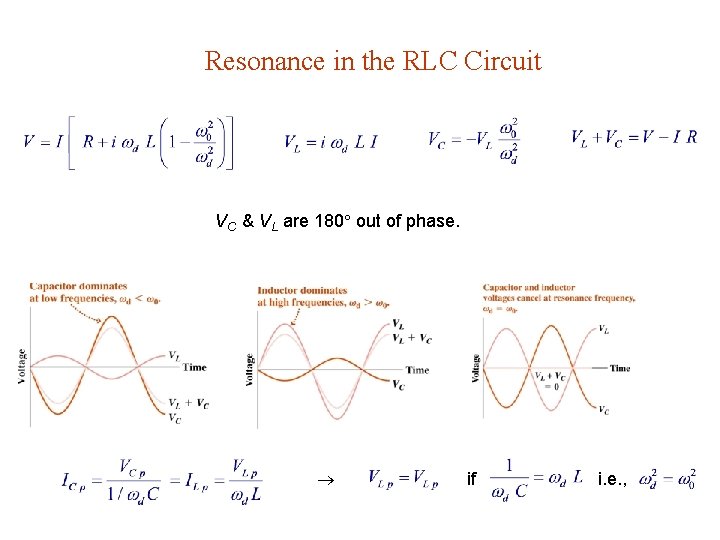
28. 4. Driven RLC Circuits & Resonance I + VR + + VL VC + Driven damped oscillator : Long time: oscillates with frequency d. Resonance if d = 0.

Resonance in the RLC Circuit VC & VL are 180 out of phase. if i. e. ,

GOT IT? 28. 3 You measure the capacitor & inductor voltage in adriven RLC circuit, and find 10 V for the rms capacitor voltage and 15 V for the rms inductor voltage. Is the driving frequency (a) above or (b) below resonance ? VCp < VLp

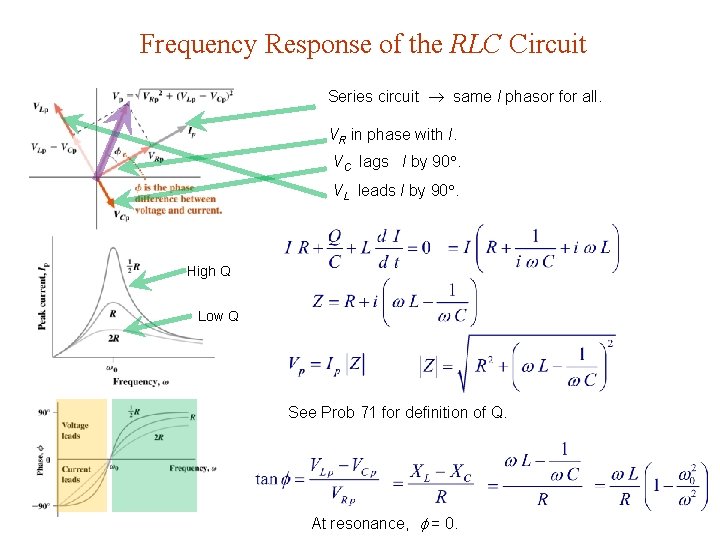
Frequency Response of the RLC Circuit Series circuit same I phasor for all. VR in phase with I. VC lags I by 90. VL leads I by 90. High Q Low Q See Prob 71 for definition of Q. At resonance, = 0.

Example 28. 4. Designing a Loud Speaker System Current flows to the midrange speaker in a loudspeaker system through a 2. 2 -m. H inductor in series with a capacitor. (a) What should the capacitance be so that a given voltage produces the greatest current at 1 k. Hz ? (b) If the same voltage produces half this current at 618 Hz, what is the speaker’s resistance ? (c) If the peak output voltage of the amplifier is 20 V, what will be the peak capacitor voltage be at 1 k. Hz ? (a) Greatest I is at resonance:

(b) If the same voltage produces half this current at 618 Hz, what is the speaker’s resistance ? At resonance: (c) If the peak output voltage of the amplifier is 20 V, what will be the peak capacitor voltage be at 1 k. Hz ? Peak voltage is at resonance (1 k. Hz).

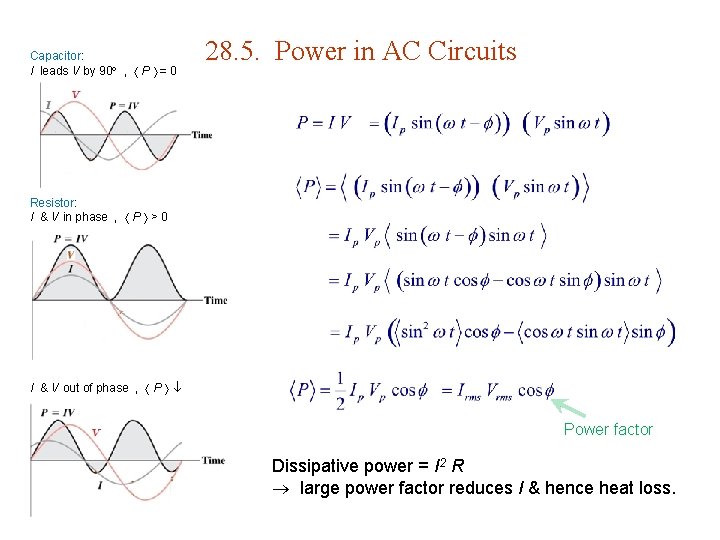
Capacitor: I leads V by 90 , P = 0 28. 5. Power in AC Circuits Resistor: I & V in phase , P > 0 I & V out of phase , P Power factor Dissipative power = I 2 R large power factor reduces I & hence heat loss.

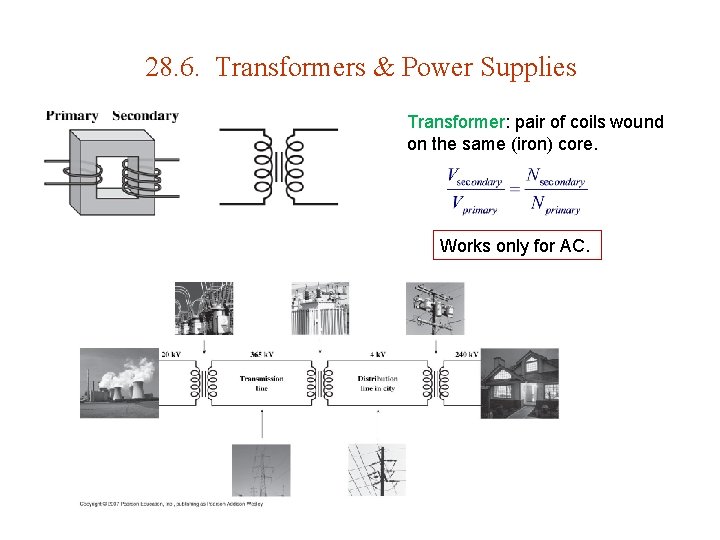
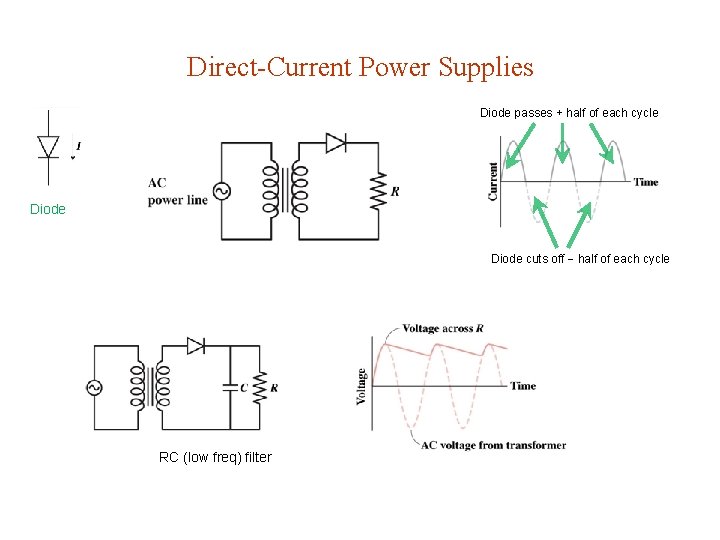
28. 6. Transformers & Power Supplies Transformer: pair of coils wound on the same (iron) core. Works only for AC.

Direct-Current Power Supplies Diode passes + half of each cycle Diode cuts off half of each cycle RC (low freq) filter