26 January 2022 Quadratic graphs of the form

26 January 2022 Quadratic graphs of the form y = a(x - p)(x - q) Lesson objective: Draw the graph of quadratic functions of the form y = a(x – p)(x – q)

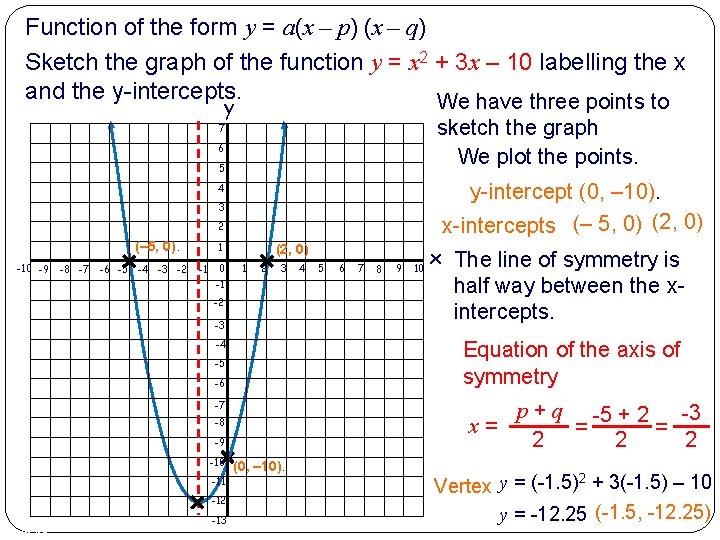
Function of the form y = a(x – p) (x – q) Sketch the graph of the function y = x 2 + 3 x – 10 labelling the x and the y-intercepts. y-intercept (0, c). y-intercept (0, – 10). We factorise the function y = x 2 + 3 x – 10 y = (x + 5)(x – 2) Factorising Writing the function y = x 2 + 3 x – 10 in the form y = a(x – p) (x – q) y = 1(x – (– 5))(x – 2) Where a=1 Roots: p = – 5 q=2 x=– 5 (– 5, 0) x-intercepts x=2 (2, 0) p and q are the roots We have three points to sketch the graph 2 of 48 = (p, 0) = (q, 0)

Function of the form y = a(x – p) (x – q) Sketch the graph of the function y = x 2 + 3 x – 10 labelling the x and the y-intercepts. We have three points to y sketch the graph We plot the points. 7 6 5 y-intercept (0, – 10). x-intercepts (– 5, 0) (2, 0) 4 3 2 (– 5, 0). -10 -9 -8 -7 -6 -5 -4 -3 -2 1 -1 0 (2, 0) 1 2 3 -1 -2 -3 -4 -6 -7 -9 -12 3 of 48 -13 6 7 8 9 10 x The line of symmetry is half way between the xintercepts. p + q -5 + 2 -3 x= = = 2 2 2 -8 -11 5 Equation of the axis of symmetry -5 -10 4 (0, – 10). 2 Vertex y = (-1. 5) + 3(-1. 5) – 10 y = -12. 25 (-1. 5, -12. 25)

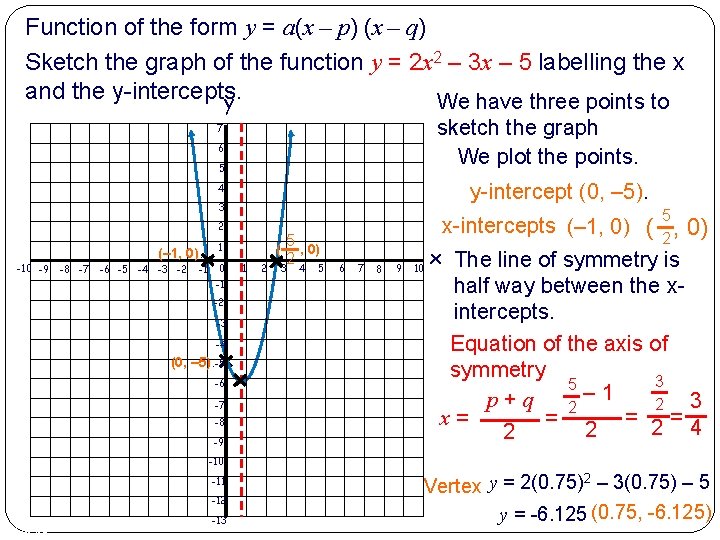
Function of the form y = a(x – p) (x – q) Sketch the graph of the function y = 2 x 2 – 3 x – 5 labelling the x and the y-intercepts. y-intercept (0, c). y-intercept (0, – 5). We factorise the function y = 2 x 2 – 3 x – 5 Factorising y = (2 x – 5)(x + 1) Writing the function y = 2 x 2 – 3 x – 5 in the form y = a(x – p) (x – q) 5 y = 2(x – 2 )(x – (– 1)) Where a=2 Roots: p= 5 5 2 q=– 1 5 x= 2 ( 2 , 0) x-intercepts x=– 1 (– 1, 0) p and q are the roots We have three points to sketch the graph 4 of 48 = (p, 0) = (q, 0)

Function of the form y = a(x – p) (x – q) Sketch the graph of the function y = 2 x 2 – 3 x – 5 labelling the x and the y-intercepts. y We have three points to sketch the graph We plot the points. 7 6 5 y-intercept (0, – 5). 4 3 5 2 (– 1, 0). -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 0 -1 -2 -3 -4 (0, – 5). -5 -6 -7 -8 -9 ( 1 2 5 , 0) 2 3 4 5 6 7 8 9 x-intercepts (– 1, 0) ( , 0) 2 x The line of symmetry is 10 half way between the xintercepts. Equation of the axis of symmetry 3 5 – 1 p+q 3 2 2 x= = 2=4 2 -10 -11 -12 5 of 48 -13 2 Vertex y = 2(0. 75) – 3(0. 75) – 5 y = -6. 125 (0. 75, -6. 125)

Function of the form y = a(x – p) (x – q) For quadratic functions in the form y = a(x – p) (x – q) Axis of symmetry is p+q x= 2 x-intercepts are (p, 0) (q, 0) y-intercept is 6 of 48 p×q×a

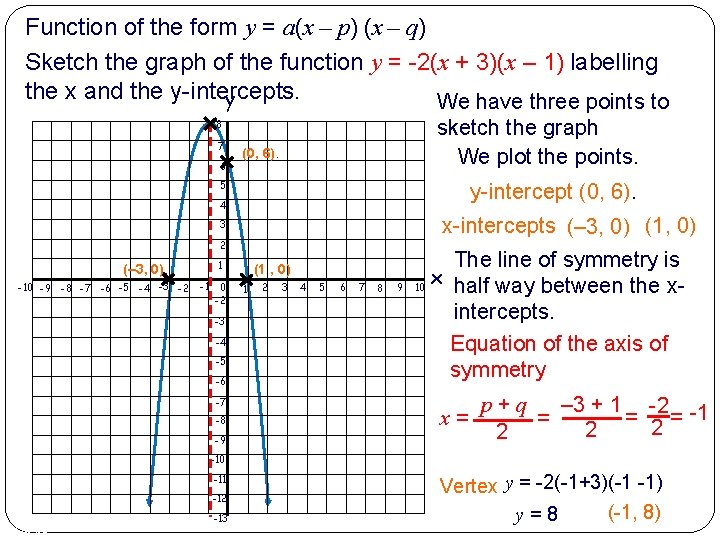
Function of the form y = a(x – p) (x – q) Sketch the graph of the function y = -2(x + 3)(x – 1) labelling the x and the y-intercepts. y We have three points to sketch the graph We plot the points. 8 7 6 (0, 6). 5 y-intercept (0, 6). 4 3 2 1 (– 3, 0). -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -2 -3 -4 -5 -6 -7 -8 -9 (1 , 0) 1 2 3 4 5 6 7 8 9 x-intercepts (– 3, 0) (1, 0) The line of symmetry is x half way between the x 10 intercepts. Equation of the axis of symmetry p+q – 3 + 1 -2 x= = 2 = -1 2 -10 -11 -12 -13 7 of 48 Vertex y = -2(-1+3)(-1 -1) (-1, 8) y=8