259 Lecture 16 Numerical Differentiation and Integration in

259 Lecture 16 Numerical Differentiation and Integration in MATLAB; Function M-files

Derivatives and Integrals o We can use MATLAB to numerically differentiate or integrate functions! o The key is to remember the definitions of derivative and definite integral: 2

Numerical Differentiation o For small x, we have the following estimate for f’(x): o Using the MATLAB commands “linspace” and “diff”, we can find reasonable approximations to f’(x), provided x is small and f is differentiable! 3

Numerical Differentiation o Example 1: o Use MATLAB to find the numerical derivative of y = sin(x) on the interval [0, 2 ]. o Compare this estimate for dy/dx to the actual derivative of y. 4

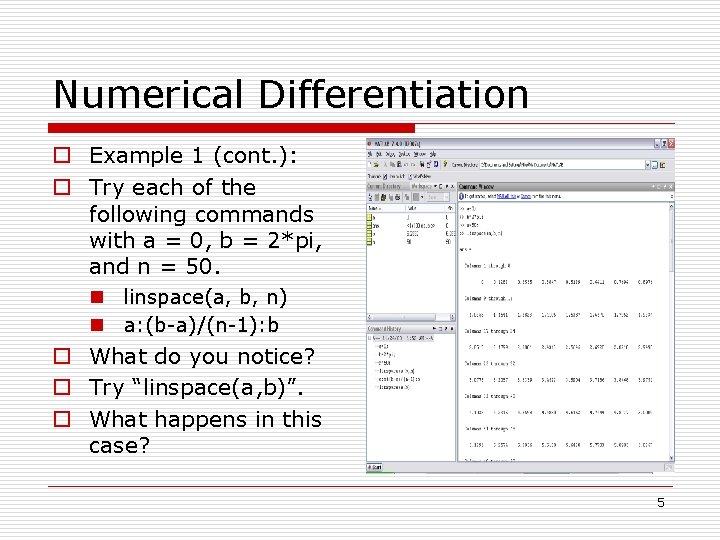
Numerical Differentiation o Example 1 (cont. ): o Try each of the following commands with a = 0, b = 2*pi, and n = 50. n linspace(a, b, n) n a: (b-a)/(n-1): b o What do you notice? o Try “linspace(a, b)”. o What happens in this case? 5

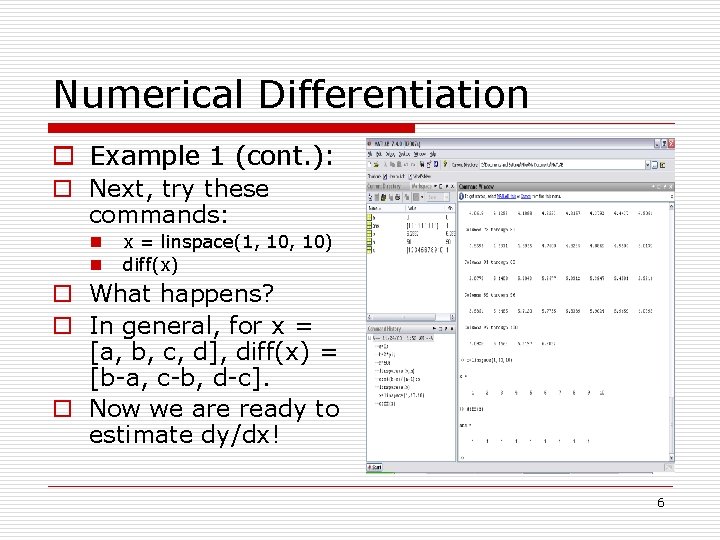
Numerical Differentiation o Example 1 (cont. ): o Next, try these commands: n n x = linspace(1, 10) diff(x) o What happens? o In general, for x = [a, b, c, d], diff(x) = [b-a, c-b, d-c]. o Now we are ready to estimate dy/dx! 6

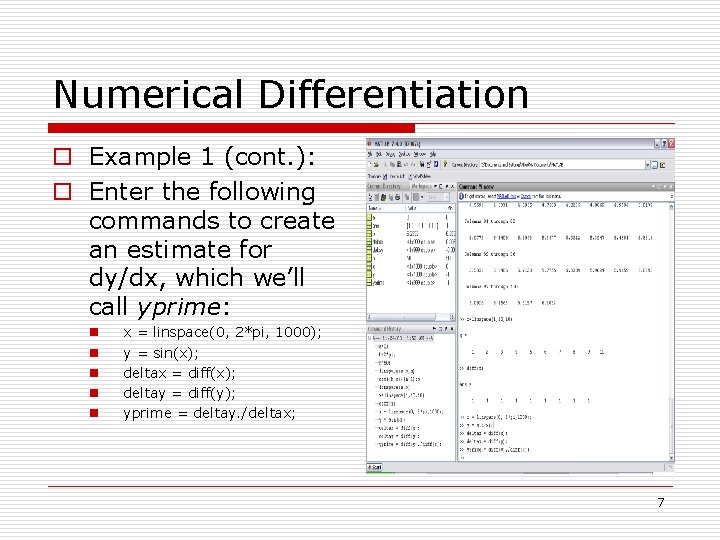
Numerical Differentiation o Example 1 (cont. ): o Enter the following commands to create an estimate for dy/dx, which we’ll call yprime: n n n x = linspace(0, 2*pi, 1000); y = sin(x); deltax = diff(x); deltay = diff(y); yprime = deltay. /deltax; 7

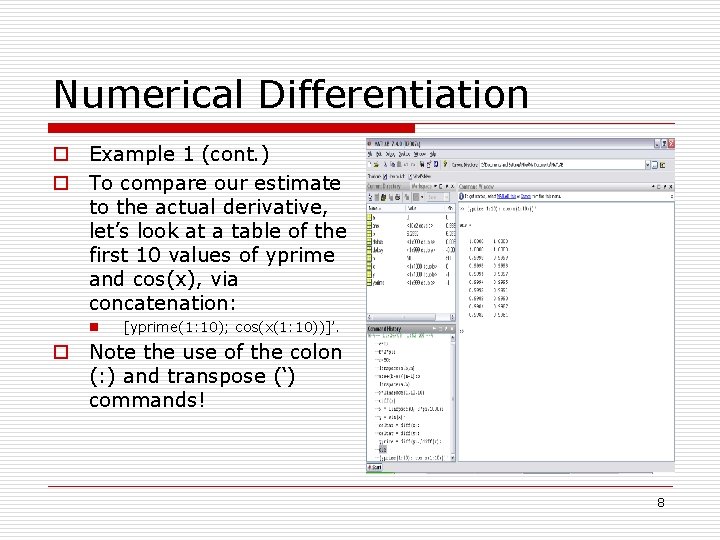
Numerical Differentiation o Example 1 (cont. ) o To compare our estimate to the actual derivative, let’s look at a table of the first 10 values of yprime and cos(x), via concatenation: n [yprime(1: 10); cos(x(1: 10))]’. o Note the use of the colon (: ) and transpose (‘) commands! 8

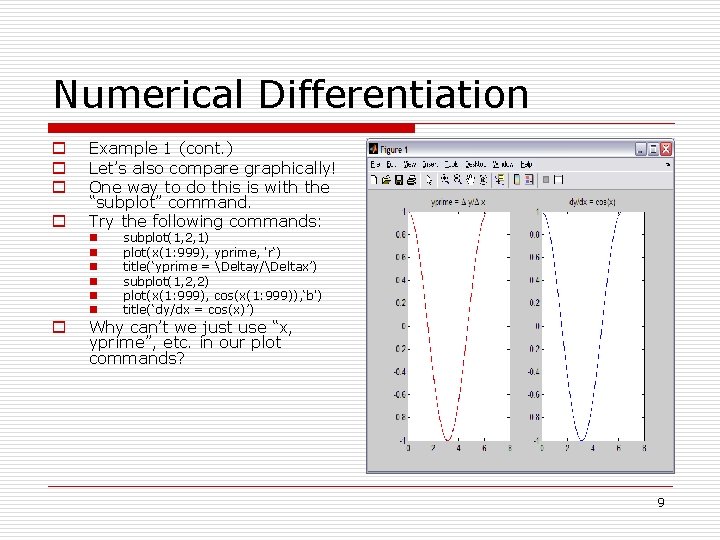
Numerical Differentiation o o Example 1 (cont. ) Let’s also compare graphically! One way to do this is with the “subplot” command. Try the following commands: n n n o subplot(1, 2, 1) plot(x(1: 999), yprime, 'r‘) title(‘yprime = Deltay/Deltax’) subplot(1, 2, 2) plot(x(1: 999), cos(x(1: 999)), ‘b') title(‘dy/dx = cos(x)’) Why can’t we just use “x, yprime”, etc. in our plot commands? 9

Numerical Integration o For integrable function f(x), choosing xi = (ba)/n and xi* to be the right endpoint of the ith subinterval, i. e. xi*=a+i*(b-a)/n, we get the following estimate for large n: o Using the “sum” command, we can find an estimate for definite integrals via Riemann sums! 10

Numerical Integration o Example 2: o Use MATLAB to numerically estimate the definite integral o Compare this estimate as n gets larger to the actual value for the integral. 11

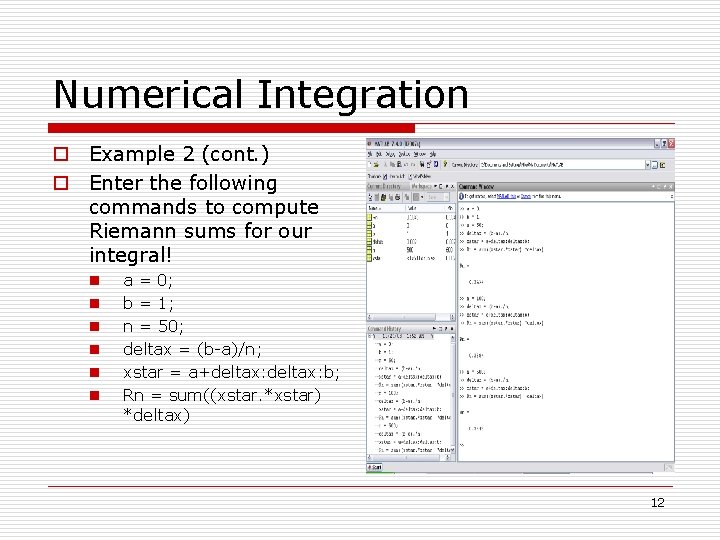
Numerical Integration o Example 2 (cont. ) o Enter the following commands to compute Riemann sums for our integral! n n n a = 0; b = 1; n = 50; deltax = (b-a)/n; xstar = a+deltax: b; Rn = sum((xstar. *xstar) *deltax) 12

Function M-Files o In addition to using M-files to run scripts, we can use them to create functions! o Function M-files can accept input and produce output. One example of a function defined by a function M-file is “linspace”. o Let’s make a function via an M-file! 13

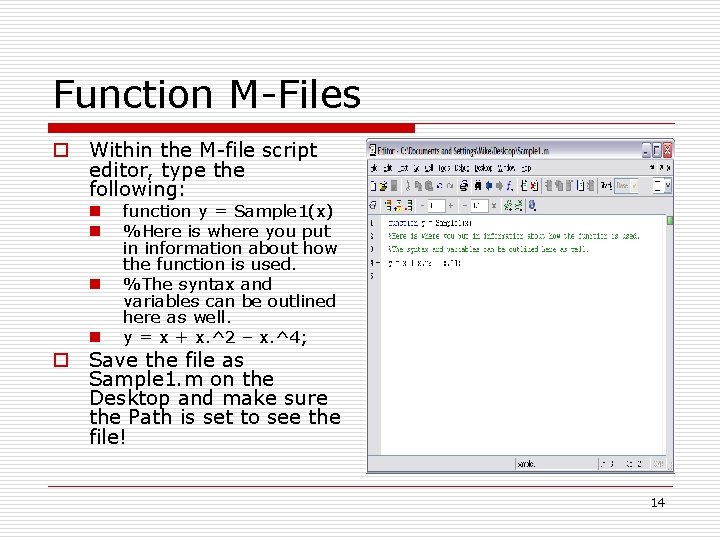
Function M-Files o Within the M-file script editor, type the following: n n function y = Sample 1(x) %Here is where you put in information about how the function is used. %The syntax and variables can be outlined here as well. y = x + x. ^2 – x. ^4; o Save the file as Sample 1. m on the Desktop and make sure the Path is set to see the file! 14

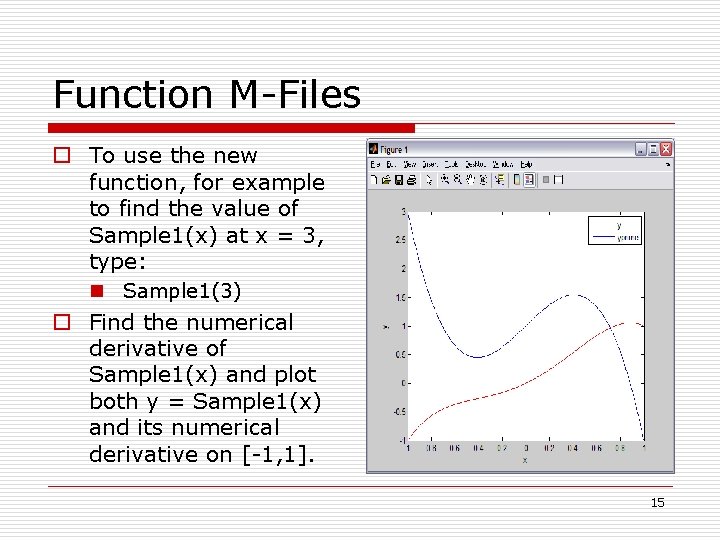
Function M-Files o To use the new function, for example to find the value of Sample 1(x) at x = 3, type: n Sample 1(3) o Find the numerical derivative of Sample 1(x) and plot both y = Sample 1(x) and its numerical derivative on [-1, 1]. 15

References o Using MATLAB in Calculus by Gary Jenson 16