25 Dot Product of Vectors Dot Product Example














- Slides: 19

25. Dot Product of Vectors

Dot Product

Example

Example

Example

Applications of dot product § Finding the angle between vectors § Determining if vectors are orthogonal (perpendicular) or parallel § Projecting a vector onto another § Work

Angle Between Two Vectors This formula comes from the law of cosines!!

Example

Example

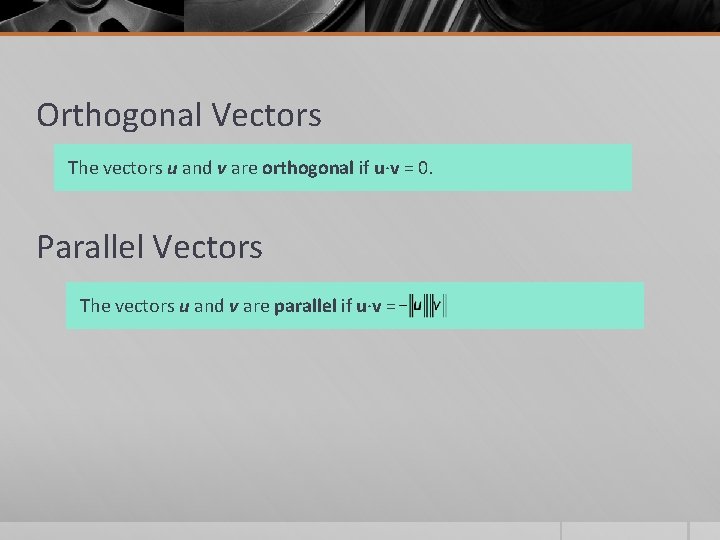
Orthogonal Vectors The vectors u and v are orthogonal if u·v = 0. Parallel Vectors The vectors u and v are parallel if u·v =

Example § Are vectors u = <2, -3> and v = <6, 4> orthogonal, parallel, or neither? § Orthogonal

Example – Tell if vectors are orthogonal, parallel, or neither

Projecting a vector onto another § We have seen applications of finding a resultant vector such as forces pulling on an object or wind resistance on a plane § There are other applications in physics and engineering where you need to do the reverse – decompose the vector into the sum of 2 perpendicular vector components

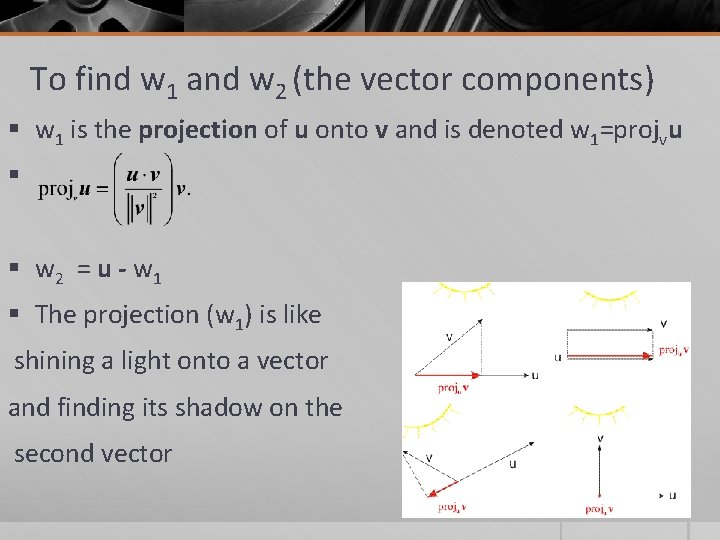
Vector components § Consider a boat on an inclined ramp shown below. The force F due to gravity pulls the boat down the ramp (w 1) and against the ramp (w 2). § Notice that w 1 and w 2 are orthogonal. These are called vector components.

To find w 1 and w 2 (the vector components) § w 1 is the projection of u onto v and is denoted w 1=projvu § § w 2 = u - w 1 § The projection (w 1) is like shining a light onto a vector and finding its shadow on the second vector

Example § Find the projection u = <3, -5> onto v = <6, 2>. Then write u as the sum of two vector components.

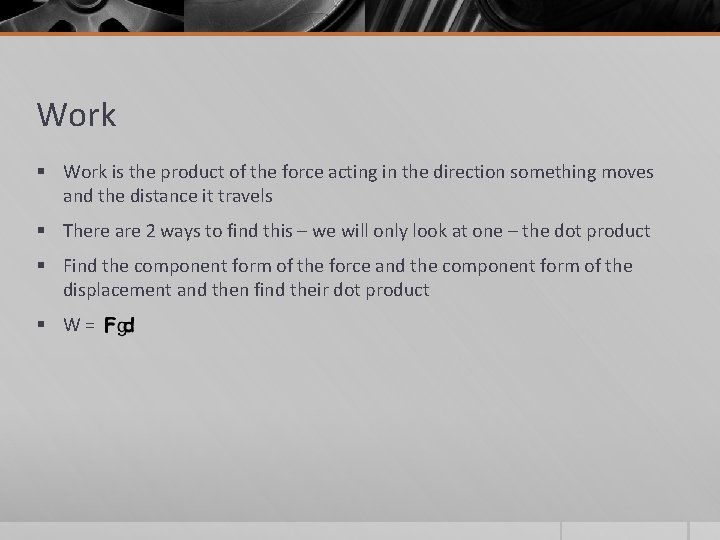
Work § Work is the product of the force acting in the direction something moves and the distance it travels § There are 2 ways to find this – we will only look at one – the dot product § Find the component form of the force and the component form of the displacement and then find their dot product § W=

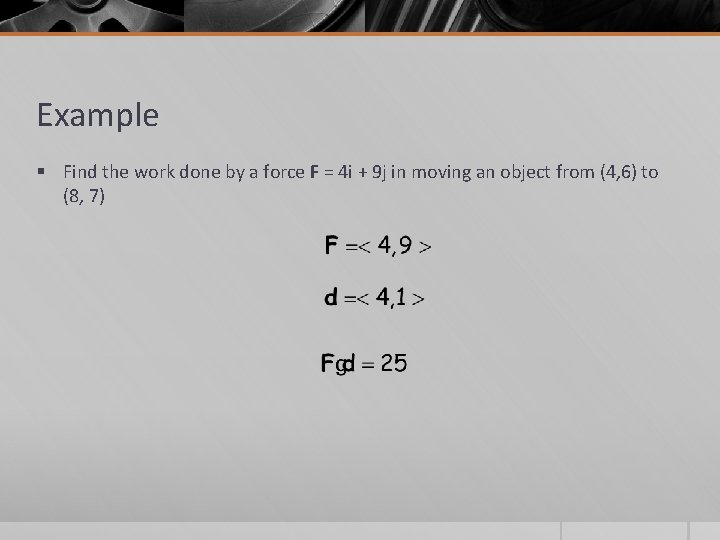
Example § Find the work done by a force F = 4 i + 9 j in moving an object from (4, 6) to (8, 7)

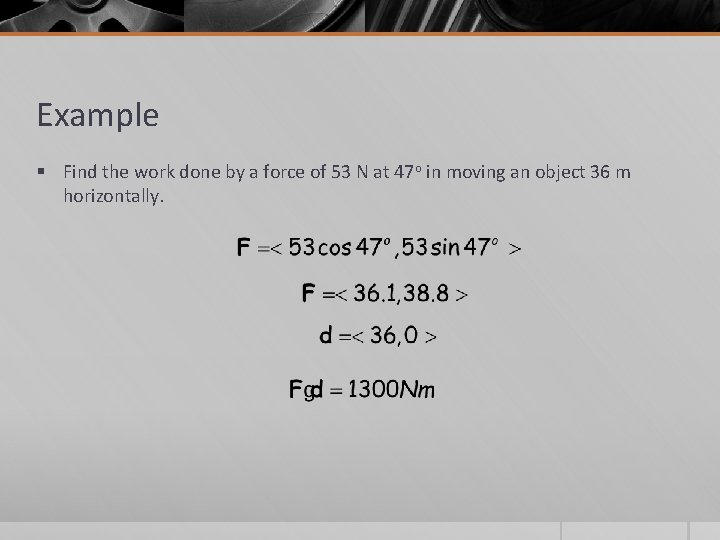
Example § Find the work done by a force of 53 N at 47 o in moving an object 36 m horizontally.