25 BASIC MATRIX OPERATIONS MATRIX A matrix is

25. BASIC MATRIX OPERATIONS

MATRIX • A matrix is a rectangular array of numbers in rows and columns.

DIMENSIONS • The dimensions of a matrix with m rows and n columns are m X n. • The matrix has 3 rows and 2 columns so the dimensions are 3 X 2.

ELEMENTS • The numbers in a matrix are its elements. • Elements are identified by their row and column. Thus, element 3, 2 is 1. 2.

EQUAL MATRICES • Equal matrices have the same dimensions and the elements in corresponding positions are equal.

SCALAR MULTIPLICATION • In matrix algebra, a real number is often called a scalar. To perform scalar multiplication, you multiply each element in the matrix by the scalar.

PROPERTIES OF MATRICES • Associative Property of Addition o(A + B) + C = A + (B + C) • Commutative Property of Addition o. A + B = B + A o We will see tomorrow that matrices do not have the commutative property of multiplication • Distributive Property of Addition/Subtraction ok(A + B) = k. A + k. B ok(A – B) = k. A – k. B

ADDING AND SUBTRACTING MATRICES • To add or subtract two matrices, simply add or subtract corresponding elements. • You can add or subtract matrices only if they have the same dimensions.

TRY THIS! • Perform the indicated operation, if possible.

TRY THIS! • Perform the indicated operations, if possible.

MULTI-STEP PROBLEM • Two pet stores sell both dogs and cats. Sales from each store for last month and this month are shown below: • Organize the data into matrices, then write and interpret a matrix giving the average monthly sales for the two month period. • Last Month: Store 1 sold 42 dogs, 33 cats. Store 2 sold 56 dogs, 21 cats. • This Month: Store 1 sold 36 dogs, 51 cats. Store 2 sold 48 dogs, 37 cats.

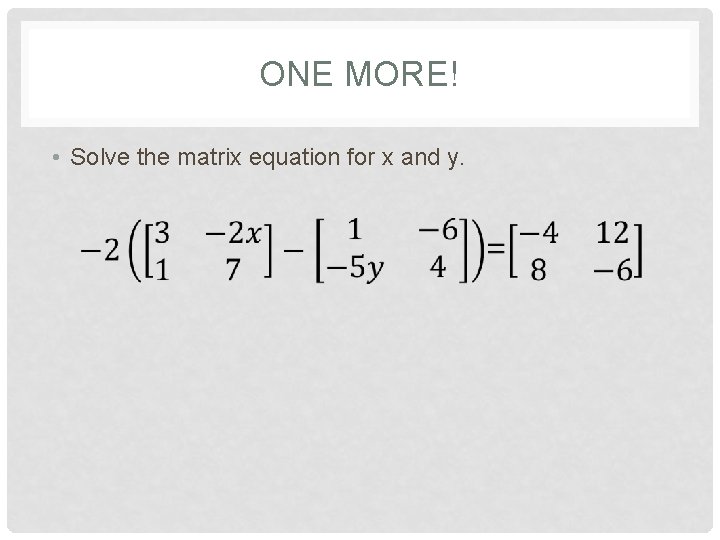
ONE MORE! • Solve the matrix equation for x and y.

ON YOUR CALCULATOR • Let’s see how to input matrices in the calculator