240 650 Principles of Pattern Recognition Montri Karnjanadecha

240 -650 Principles of Pattern Recognition Montri Karnjanadecha montri@coe. psu. ac. th http: //fivedots. coe. psu. ac. th/~montri 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 1

Chapter 3 Maximum-Likelihood and Bayesian Parameter Estimation 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 2

Introduction • We could design an optimum classifier if we know P(wi) and p(x|wi) • We rarely have knowledge about the probabilistic structure of the problem • We often estimate P(wi) and p(x|wi) from training data or design samples 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 3

Maximum-Likelihood Estimation • ML Estimation • Always have good convergence properties as the number of training samples increases • Simpler that other methods 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 4

The General Principle • Suppose we separate a collection of samples according to class so that we have c data sets, D 1, …, Dc with the samples in Dj having been drawn independently according to the probability law p(x|wj) • We say such samples are i. i. d. – independently and identically distributed random variable 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 5

The General Principle • We assume that p(x|wj) has a known parametric form and is determined uniquely by the value of a parameter vector qj • For example • We explicitly write p(x|wj) as p(x|wj, qj) 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 6

Problem Statement • To use the information provided by the training samples to obtain good estimates for the unknown parameter vectors q 1, …qc associated with each category 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 7

Simplified Problem Statement • If samples in Di give no information about qj if i=j • We now have c separated problems of the following form: To use a set D of training samples drawn independently from the probability density p(x|q) to estimate the unknown vector q. 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 8

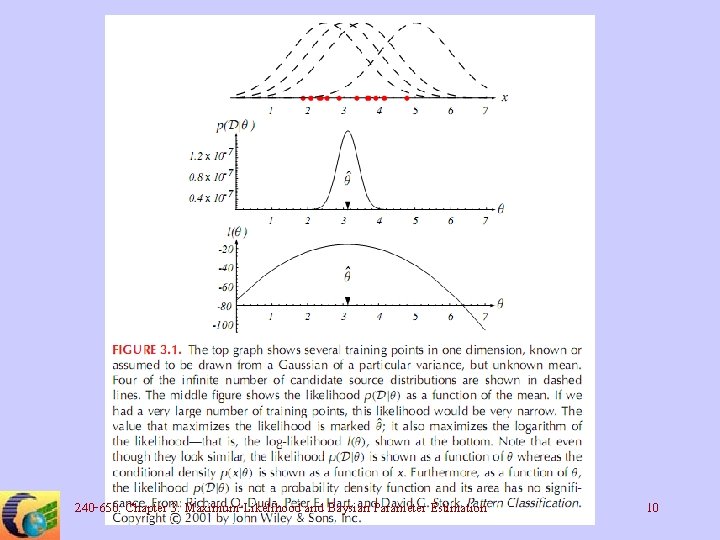
• Suppose that D contains n samples, x 1, …, xn. • Then we have Likelihood of q with respect to the set of samples • The Maximum-Likelihood estimate of q is the value of that maximizes p(D|q) 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 9

240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 10

• Let q = (q 1, …, qp)t • Let be the gradient operator 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 11

Log-Likelihood Function • We define l(q) as the log-likelihood function • We can write our solution as 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 12

MLE • From • We have • And • Necessary condition for MLE 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 13

The Gaussian Case: Unknown m • Suppose that the samples are drawn from a multivariate normal population with mean m and covariance matrix S • Let m is the only unknown • Consider a sample point xk and find • and 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 14

• The MLE of m must satisfy • After rearranging 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 15

Sample Mean • The MLE for the unknown population meanis just the arithmetic average of the training samples (or sample mean) • If we think of the n samples as a cloud of points, then the sample mean is the centroid of the cloud 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 16

The Gaussian Case: Unknown m and S • This is a more typical case where mean and covariance matrix are unknown • Consider the univariate case with q 1=m and q 2=s 2 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 17

• And its derivative is • Set to 0 • and 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 18

• With a little rearranging, we have 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 19

MLE for multivariate case 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 20

Bias • The MLE for the variance s 2 is biased • The expected value over all data sets of size n of the sample variance is not equal to the true variance • An Unbiased estimator for S is given by 240 -650: Chapter 3: Maximum-Likelihood and Baysian Parameter Estimation 21