22 Electric Potential 1 2 3 4 Electric

22. Electric Potential 1. 2. 3. 4. Electric Potential Difference Calculating Potential Difference & the Electric Field Charged Conductors

n This parasailer landed on a 138, 000 -volt power line. Why didn’t he get electrocuted? He touches only 1 line – there’s no potential differences & hence no energy transfer involved.

22. 1. Electric Potential Difference Conservative force: ( path independent ) Electric potential difference electric potential energy difference per unit charge [ V ] = J/C = Volt = V if reference potential VA = 0. For a uniform field: r. AB E

Table 22. 1. Force & Field, Potential Energy & Electric Potential Quantity Force Electric field Potential energy difference Electric potential difference Symbol / Equation F E=F/q Units N N/C or V/m J J/C or V

Potential Difference is Path Independent Potential difference VAB depends only on positions of A & B. Calculating along any paths (1, 2, or 3) gives VAB = E r.

GOT IT? 22. 1 What would happen to VAB in the figure if doubles becomes 0 (a) E were doubled; (b) r were doubled; (c) the points were moved so the path lay at right angles to E; reverses sign (d) the positions of A & B are interchanged.

The Volt & the Electronvolt [ V ] = J/C = Volt = V E. g. , for a 12 V battery, 12 J of work is done on every 1 C charge that moves from its negative to its positive terminals. Voltage = potential difference when no B(t) is present. Electronvolt (e. V) = energy gained by a particle carrying 1 elementary charge when it moves through a potential difference of 1 volt. 1 elementary charge = 1. 6 10 19 C = e 1 e. V = 1. 6 10 19 J

Table 22. 2. Typical Potential Differences Between human arm & leq due to heart’s electrical activity 1 m. V Across biological cell membrane 80 m. V Between terminals of flashlight battery 1. 5 V Car battery 12 V Electric outlet (depends on country) 100 -240 V Between lon-distance electric transmission line & ground 365 k. V Between base of thunderstorm cloud & ground 100 MV

INTERNATIONAL VOLTAGE Afghanistan Australia Bahamas Brazil Canada China Finland Guam Hong. Kong Japan Mexico Spain United Kingdom United States Vietnam 220 V 240 V 120/220 V 120 V 230 V 110 V 220 V 100 V 127 V 230 V 120 V 127/220 V

GOT IT? 22. 2 10 e. V (a) A proton ( charge e ), 20 e. V (b) an particle ( charge 2 e ), and 10 e. V (c) a singly ionized O atom each moves through a 10 -V potential difference. What’s the work in e. V done on each?

Example 22. 1. X Rays In an X-ray tube, a uniform electric field of 300 k. N/C extends over a distance of 10 cm, from an electron source to a target; the field points from the target towards the source. Find the potential difference between source & target and the energy gained by an electron as it accelerates from source to target ( where its abrupt deceleration produces X-rays ). Express the energy in both electronvolts & joules.

Example 22. 2. Charged Sheet An isolated, infinite charged sheet carries a uniform surface charge density . Find an expression for the potential difference from the sheet to a point a perpendicular distance x from the sheet. E

Curved Paths & Nonuniform Fields Staight path, uniform field: Curved path, nonuniform field:

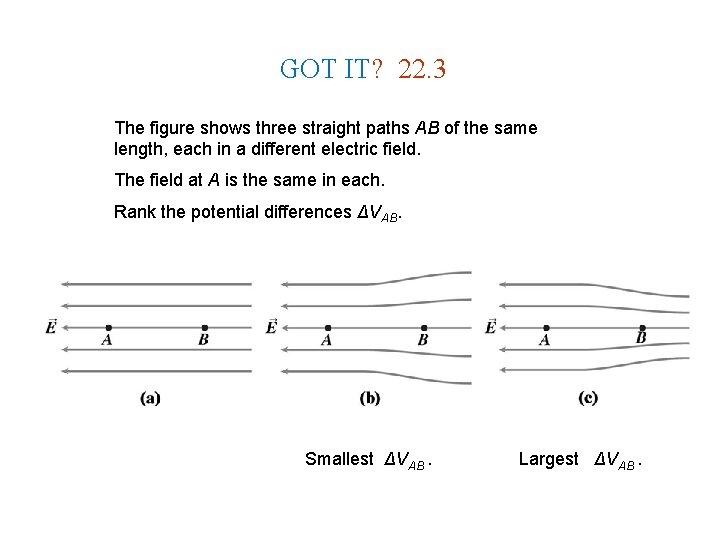
GOT IT? 22. 3 The figure shows three straight paths AB of the same length, each in a different electric field. The field at A is the same in each. Rank the potential differences ΔVAB. Smallest ΔVAB. Largest ΔVAB.

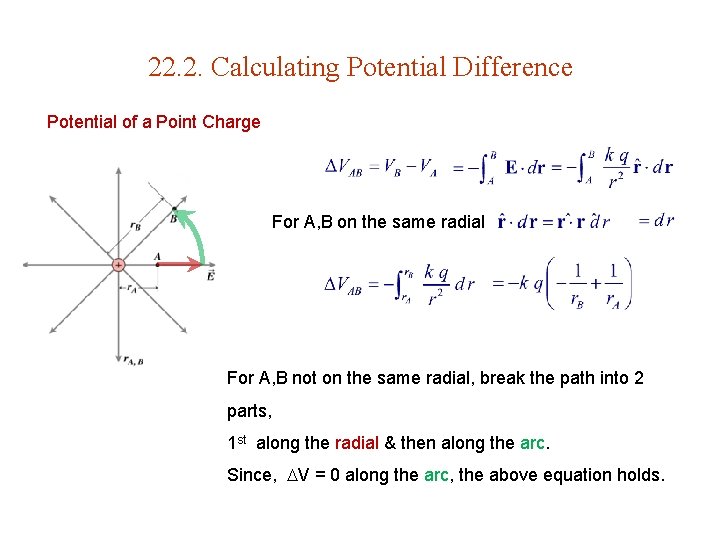
22. 2. Calculating Potential Difference Potential of a Point Charge For A, B on the same radial For A, B not on the same radial, break the path into 2 parts, 1 st along the radial & then along the arc. Since, V = 0 along the arc, the above equation holds.

The Zero of Potential Only potential differences have physical significance. Simplified notation: R = point of zero potential VA = potential at A. Some choices of zero potential Power systems / Circuits Automobile electric systems Isolated charges Earth ( Ground ) Car’s body Infinity

GOT IT? 22. 4 You measure a potential difference of 50 V between two points a distance 10 cm apart in the field of a point charge. If you move closer to the charge and measure the potential difference over another 10 -cm interval, will it be (a) greater, (b) less, or (c) the same?

Example 22. 3. Science Museum The Hall of Electricity at the Boston Museum of Science contains a large Van de Graaff generator, a device that builds up charge on a metal sphere. The sphere has radius R = 2. 30 m and develops a charge Q = 640 C. Considering this to be a single isolate sphere, find (a) the potential at its surface, (b) the work needed to bring a proton from infinity to the sphere’s surface, (c) (a) (b) (c) the potential difference between the sphere’s surface & a point 2 R from its center.

Example 22. 4. High Voltage Power Line A long, straight power-line wire has radius 1. 0 cm & carries line charge density = 2. 6 C/m. Assuming no other charges are present, what’s the potential difference between the wire & the ground, 22 m below?

Finding Potential Differences Using Superposition Potential of a set of point charges: Potential of a set of charge sources:

Example 22. 5. Dipole Potential An electric dipole consists of point charges q a distance 2 a apart. Find the potential at an arbitrary point P, and approximate for the casewhere the distance to P is large compared with the charge separation. +q: hill r >> a V=0 q: hole p = 2 qa = dipole moment

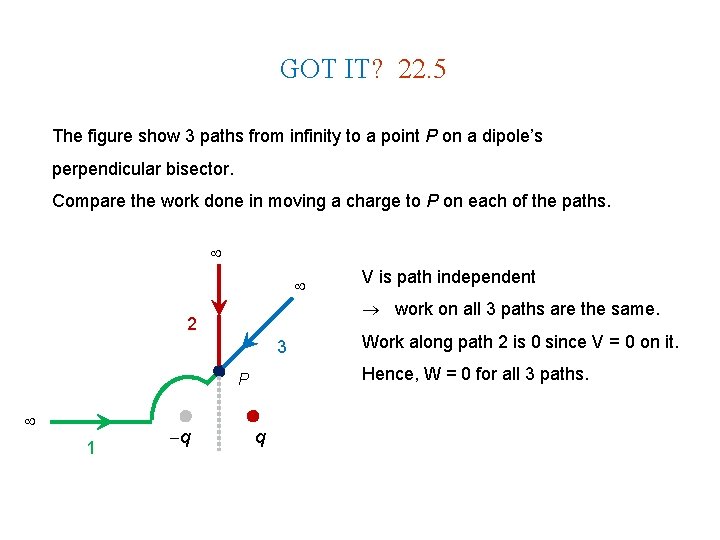
GOT IT? 22. 5 The figure show 3 paths from infinity to a point P on a dipole’s perpendicular bisector. Compare the work done in moving a charge to P on each of the paths. work on all 3 paths are the same. 2 3 1 q Work along path 2 is 0 since V = 0 on it. Hence, W = 0 for all 3 paths. P V is path independent q

Continuous Charge Distributions Superposition:

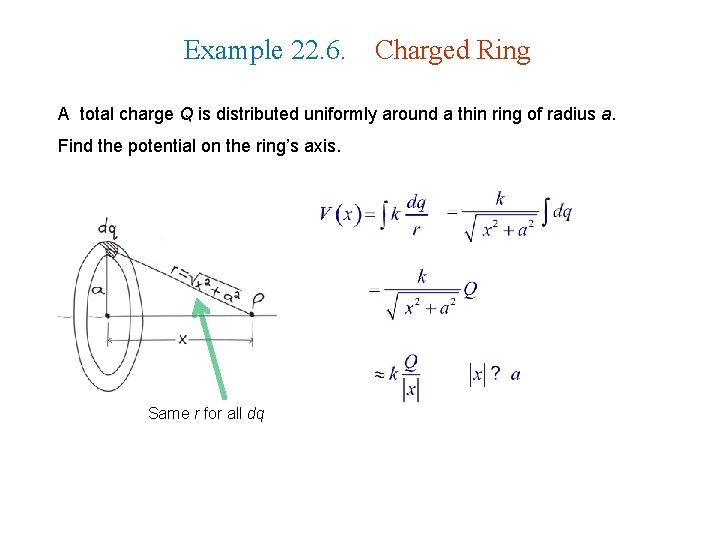
Example 22. 6. Charged Ring A total charge Q is distributed uniformly around a thin ring of radius a. Find the potential on the ring’s axis. Same r for all dq

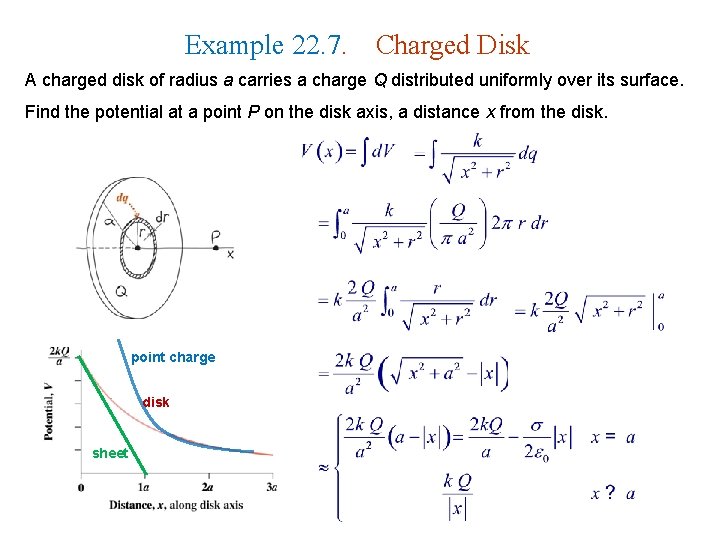
Example 22. 7. Charged Disk A charged disk of radius a carries a charge Q distributed uniformly over its surface. Find the potential at a point P on the disk axis, a distance x from the disk. point charge disk sheet

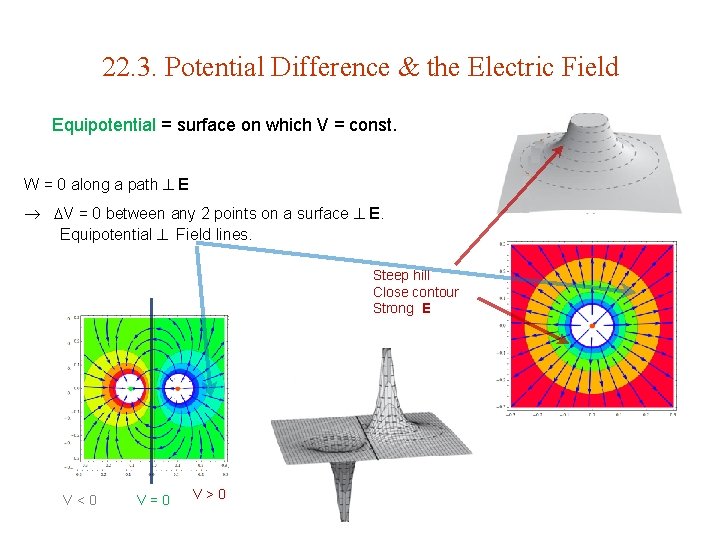
22. 3. Potential Difference & the Electric Field Equipotential = surface on which V = const. W = 0 along a path E V = 0 between any 2 points on a surface E. Equipotential Field lines. Steep hill Close contour Strong E V<0 V=0 V>0

GOT IT? 22. 6 The figure show cross sections through 2 equipotential surfaces. In both diagrams, the potential difference between adjacent equipotentials is the same. Which could represent the field of a point charge? Explain. (a). Potential decreases as r 1 , so the spacings between equipotentials should increase with r.

Calculating Field from Potential = ( Gradient of V ) E is strong where V changes rapidly ( equipotentials dense ).

Example 22. 8. Charged Disk Use the result of Example 22. 7 to find E on the axis of a charged disk. Example 22. 7: x>0 x<0 dangerous conclusion

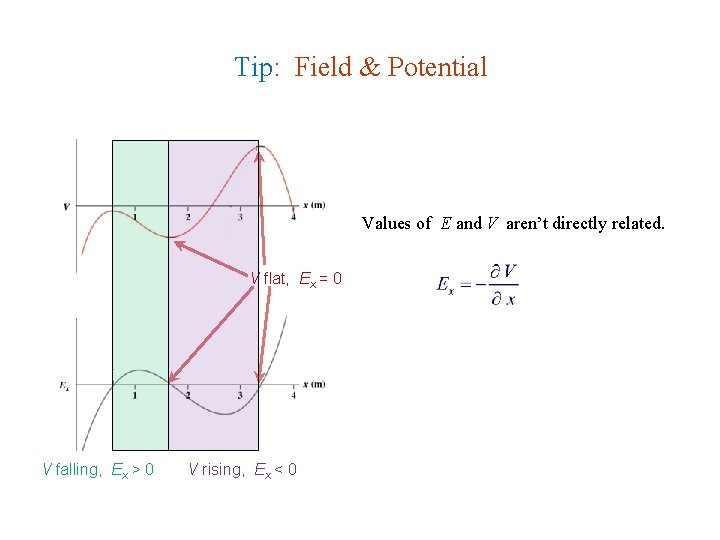
Tip: Field & Potential Values of E and V aren’t directly related. V flat, Ex = 0 V falling, Ex > 0 V rising, Ex < 0

22. 4. Charged Conductors In electrostatic equilibrium, E=0 inside a conductor. E// = 0 on surface of conductor. W = 0 for moving charges on / inside conductor. The entire conductor is an equipotential. Consider an isolated, spherical conductor of radius R and charge Q. Q is uniformly distributed on the surface E outside is that of a point charge Q. V(r) = k Q / R. for r R.

Consider 2 widely separated, charged conducting spheres. Their potentials are Same V If we connect them with a thin wire, there’ll be charge transfer until V 1 = V 2 , i. e. , In terms of the surface charge densities we have Smaller sphere has higher field at surface.

Conceptual Example 22. 1. An Irregular Condutor Sketch some equipotentials & electric field lines for an isolated egg-shaped conductor. Ans. Surface is equipotential | E | is larger where curvature of surface is large. More field lines emerging from sharply curved regions. From afar, conductor is like a point charge.

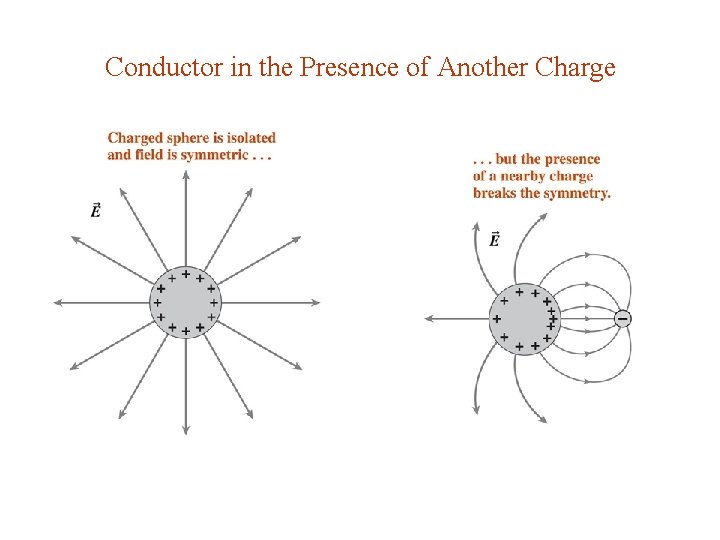
Conductor in the Presence of Another Charge

Making the Connection The potential difference between the conductor and the outermost equipotential shown in figure is 70 V. Determine approximate values for the strongest & weakest electric fields in the region, assuming it is drawn at the sizes shown. Strongest field : Weakest field : 7 mm 12 mm

Application: Corona Discharge, Pollution Control, and Xerography Air ionizes for E > MN/C. Recombination of e with ion Corona discharge ( blue glow ) Electrostatic precipitators: Removes pollutant particles (up to 99%) using gas ions produced by Corona discharge across power-line insulator. Corona discharge. Laser printer / Xerox machines: Ink consists of plastic toner particles that adhere to charged regions on lightsensitive drum, which is initially charged uniformy by corona discharge.