22 December 2021 The domain and range of

22 December 2021 The domain and range of a relation LO: To be able to identify the domain and the range of a relation. To write the domain and the range of a function using intervals or set builder notation. www. mathssupport. org

Domain and range n n The domain is the set of all the first numbers (x-values) of the ordered pairs The range is the set the second numbers (y-values) of the ordered pairs www. mathssupport. org

Interval Notation You can often write the domain and range of a relation using interval notation Interval notation uses only five symbols Round Brackets Square Brackets Infinity Negative Infinity Union www. mathssupport. org () [] ∞ -∞

Interval Notation Use the round brackets ( , ) if the value at this side is not included in the graph Example: (-∞, 4) means: all the real numbers less than 4, but 4 is not included. Use the square brackets [ , ] if the value at this side is included in the graph. Example: [-3, 5] means: al the real numbers between -3 and 5 including both. www. mathssupport. org

Interval Notation If the graph goes forever to the left, the domain (x-values) starts with (-∞. For example, The domain is the set of numbers that are all less than 3, including 3. You can write the inequality x 3 You can write in interval notation (-∞, 3] www. mathssupport. org

Interval Notation If the graph goes forever to the right, the domain (x-values) ends with ∞). For example, The domain is the set of numbers that are all greater than -5. You can write the inequality x -5 You can write in interval notation (-5, ∞) www. mathssupport. org

Interval Notation If the graph goes downwards forever, the range (y-values) starts with (-∞. For example, The range is the set of numbers that are all less than 2. You can write the inequality y 2 You can write in interval notation (-∞, 2) www. mathssupport. org

Interval Notation If the graph goes up forever, the range (y-values) ends with ∞). For example, The range is the set of numbers that are all greater than 0, including 0. You can write the inequality y 0 You can write in interval notation [0, ∞) www. mathssupport. org
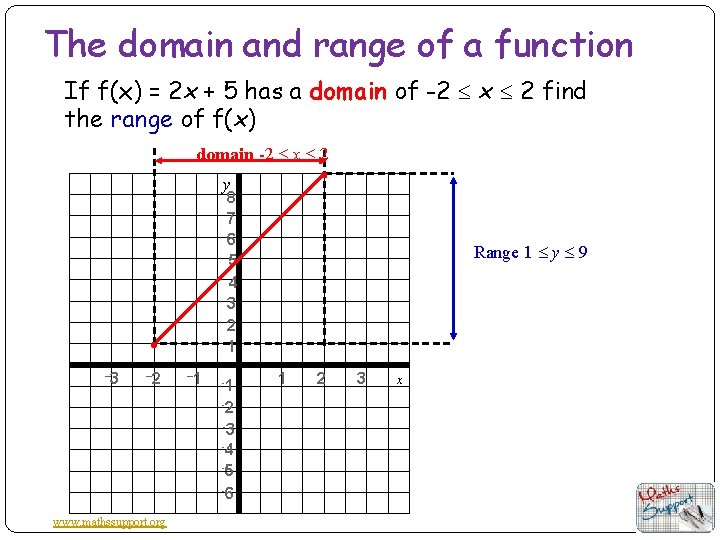
The domain and range of a function If f(x) = 2 x + 5 has a domain of -2 x 2 find the range of f(x) domain -2 x 2 y 8 7 6 5 4 3 2 1 – 3 – 2 – 1 -1 -2 -3 -4 -5 -6 www. mathssupport. org Range 1 y 9 1 2 3 x
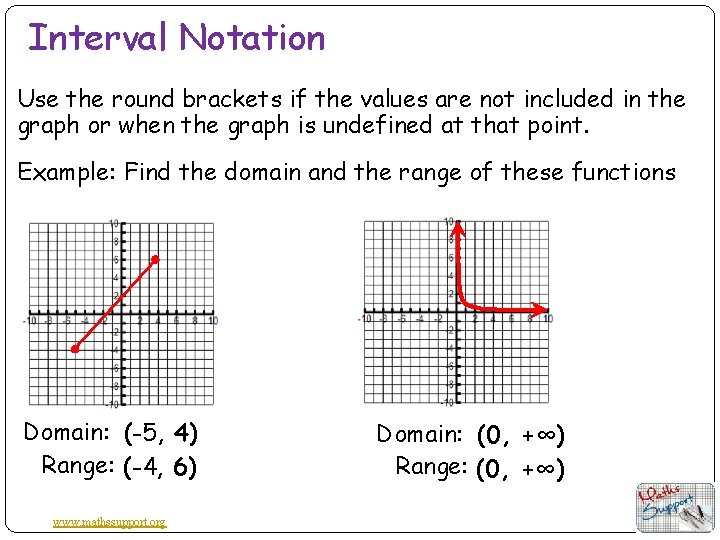
Interval Notation Use the round brackets if the values are not included in the graph or when the graph is undefined at that point. Example: Find the domain and the range of these functions Domain: (-5, 4) Range: (-4, 6) www. mathssupport. org Domain: (0, +∞) Range: (0, +∞)
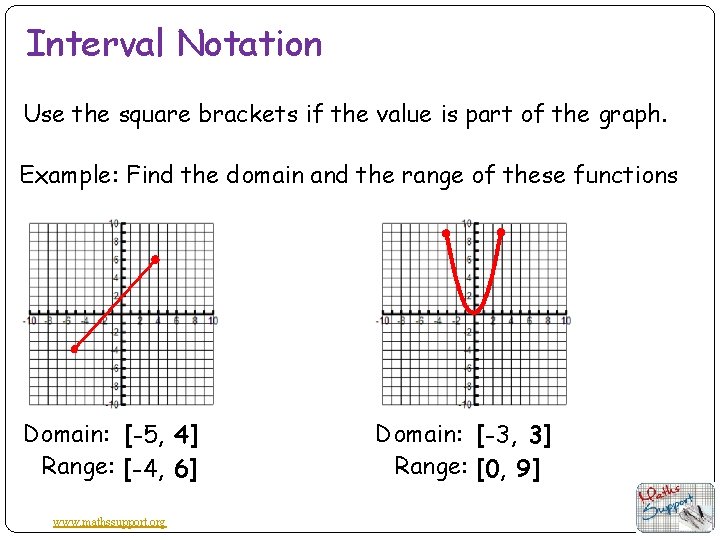
Interval Notation Use the square brackets if the value is part of the graph. Example: Find the domain and the range of these functions Domain: [-5, 4] Range: [-4, 6] www. mathssupport. org Domain: [-3, 3] Range: [0, 9]

Interval Notation Whenever there is a break in the values, write the interval up to the point. Then write another interval for the values after that point. Put a union sign between each interval to join them together Domain: [-8, 1) [3, +∞] Range: (-∞, 6] www. mathssupport. org

Asymptotes An asymptote is a line that a graph approaches but does not intersect. For example, in the graph of y = x 1 The line approaches the x-axis (y = 0), but never touches it. As we go to infinity the line will not actually reach y = 0 but will always get closer and closer. 1 y= x The x-axis or y = 0 is called the horizontal asymptote The y-axis or x = 0 is called the vertical asymptote for the same reason. www. mathssupport. org
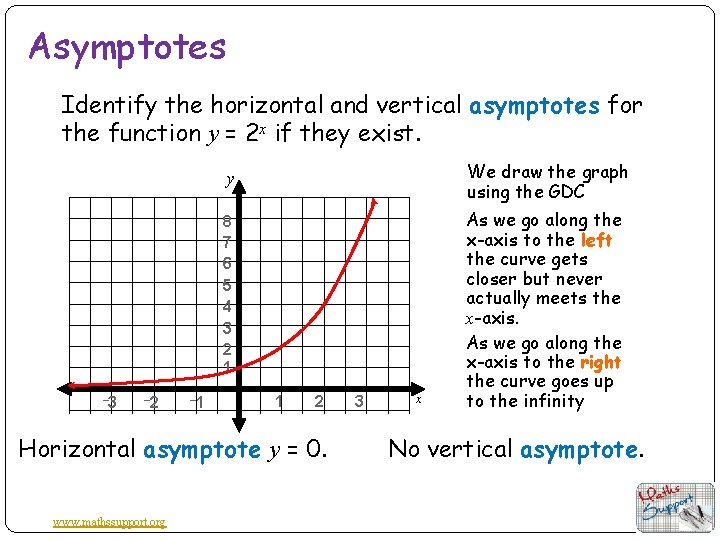
Asymptotes Identify the horizontal and vertical asymptotes for the function y = 2 x if they exist. We draw the graph using the GDC y 8 7 6 5 4 3 2 1 – 3 – 2 – 1 1 2 Horizontal asymptote y = 0. www. mathssupport. org 3 x As we go along the x-axis to the left the curve gets closer but never actually meets the x-axis. As we go along the x-axis to the right the curve goes up to the infinity No vertical asymptote.
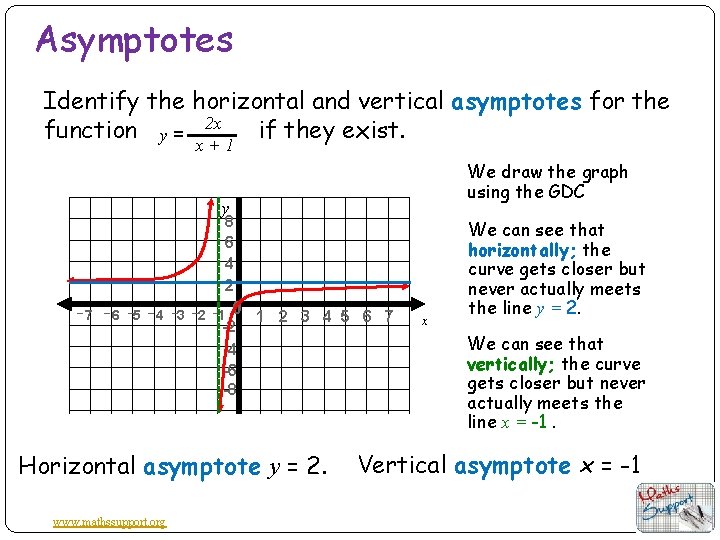
Asymptotes Identify the horizontal and vertical asymptotes for the function y = 2 x if they exist. x+1 We draw the graph using the GDC y 8 6 4 2 – 7 – 6 – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 6 7 -2 -4 -6 -8 Horizontal asymptote y = 2. www. mathssupport. org x We can see that horizontally; the curve gets closer but never actually meets the line y = 2. We can see that vertically; the curve gets closer but never actually meets the line x = -1. Vertical asymptote x = -1

Set builder notation A shorthand used to write sets, often sets with an infinite number of elements. In set builder notation we use curly brackets { }, variables and other symbols to express the domain and range. The set of Less than or equal to Greater than or equal to Is a member of the set of real numbers Union (or) Such that www. mathssupport. org {} < ≤ > ℝ :

Set builder notation What is the meaning of the following expression written in set builder notation? {x : x ≤ 5} The set of x-values Such that x is less than or equal to 5 Interval notation Description Set builder notation x is less than 3 -4 or-5 greater than lies between and 2 toincluding greater -5} than or equal 3 3] (-5, +∞) {x : x ≤> ≤ 3} (-∞, 3) [6, +∞) x is less x<3, 6} [-4, 2) -4 xx > 2} or equal 4 but notto 2 6 www. mathssupport. org

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org www. mathssupport. org
- Slides: 18