2016 Kappa Electronics Motor Control Training Series V

2016 Kappa Electronics Motor Control Training Series V 3 = 010 d-axis © 2016 Kappa Electronics LLC V 2 = 110 Sector 2 Vref Sector 3 V 4 = 011 V 1 = 100 T 1 • V 1 T 2 • V 2 q-axis Sector 6 Sector 4 Sector 5 V 5 = 001 V 6 = 101 -Vth Dave Wilson Co-Owner Kappa Electronics www. kappaiq. com

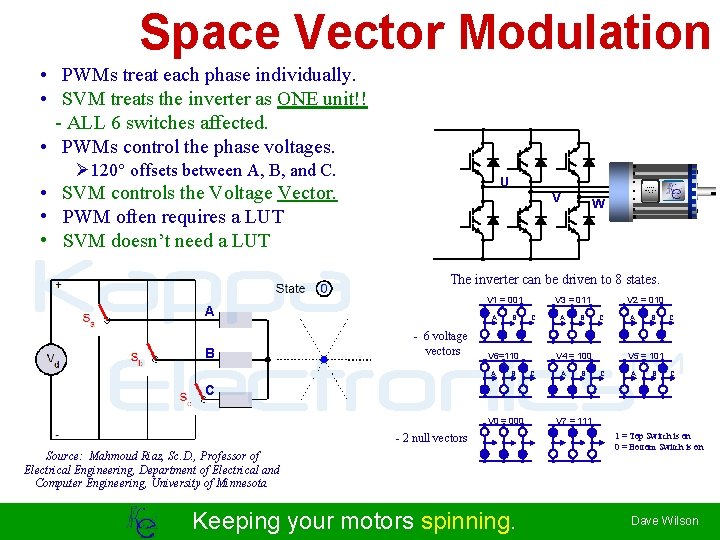
Space Vector Modulation • PWMs treat each phase individually. • SVM treats the inverter as ONE unit!! - ALL 6 switches affected. • PWMs control the phase voltages. Ø 120° offsets between A, B, and C. U • SVM controls the Voltage Vector. • PWM often requires a LUT • SVM doesn’t need a LUT Dave’s Motor Control Center V W Kappa TM Electronics The inverter can be driven to 8 states. V 1 = 001 A B A - 6 voltage vectors B C V 6=110 A B V 2 = 010 V 3 = 011 A B C V 4 = 100 C A B C V 5 = 101 C A B C C V 0 = 000 - 2 null vectors Source: Mahmoud Riaz, Sc. D. , Professor of Electrical Engineering, Department of Electrical and Computer Engineering, University of Minnesota Keeping your motors spinning. V 7 = 111 1 = Top Switch is on 0 = Bottom Switch is on Dave Wilson

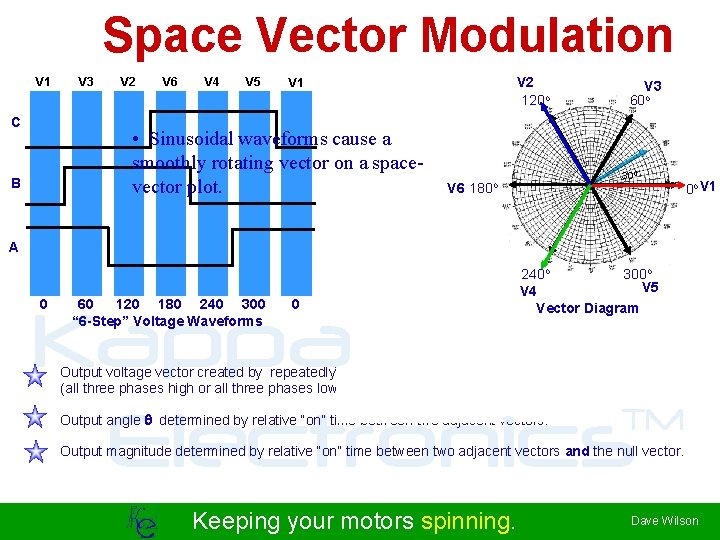
Space Vector Modulation V 1 C V 3 V 2 V 6 V 4 V 5 • Sinusoidal waveforms cause a smoothly rotating vector on a spacevector plot. B V 2 120 o V 1 V 3 60 o 300 V 6 180 o 0 o V 1 A 0 60 120 180 240 300 “ 6 -Step” Voltage Waveforms 0 300 o 240 o V 5 V 4 Vector Diagram Kappa TM Electronics Output voltage vector created by repeatedly switching between adjacent vectors and the “null” vector (all three phases high or all three phases low). Output angle determined by relative “on” time between two adjacent vectors. Output magnitude determined by relative “on” time between two adjacent vectors and the null vector. Keeping your motors spinning. Dave Wilson

SVM Implementation V 3 = 011 (Vy) V 2 = 010 • Vref is created by adding two adjacent voltage vectors (Vx, Vy) plus a null vector in a time averaging fashion: Vref = Vx • T 1 + Vy • T 2 + Vnull • T 0 Where: Sector 2 Vref Sector 3 V 6 = 110 Vx = lower angle (CW) voltage vector Vy = higher angle (CCW) voltage vector T 2 • Vy V 1 = 001 (Vx) T 1 • Vx Sector 4 Sector 6 Sector 5 If Vref is represented in POLAR notation ( T 1 = T • m • SIN(60 - ) T 2 = T • m • SIN( ) T 0 = T - T 1 - T 2 ): V 5 = 101 V 4 = 100 Example vector reconstruction in sector 1. Kappa TM Electronics SWITCHING PERIOD T m = normalized vector magnitude (0 to 1) = vector angle between Vref and Vx (0 to 60 o) T = SVM switching period Vx Vy Null T 1 T 2 T 0 Keeping your motors spinning. Dave Wilson

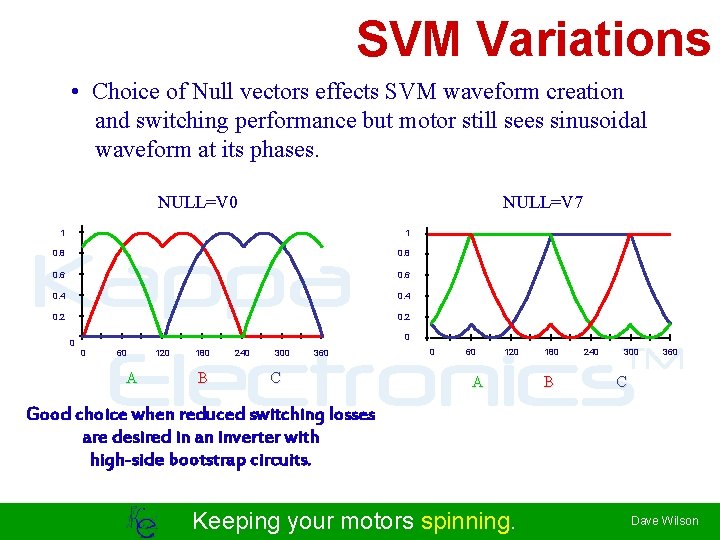
SVM Variations • Choice of Null vectors effects SVM waveform creation and switching performance but motor still sees sinusoidal waveform at its phases. NULL=V 7 NULL=V 0 1 1 Kappa TM Electronics 0. 8 0. 6 0. 4 0. 2 0 0 0 60 A 120 180 B 240 300 360 C 0 60 120 A 180 B 240 300 360 C Good choice when reduced switching losses are desired in an inverter with high-side bootstrap circuits. Keeping your motors spinning. Dave Wilson

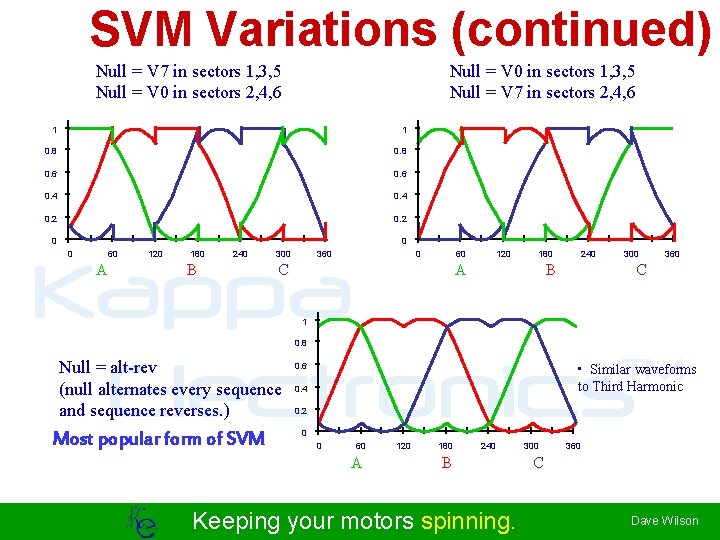
SVM Variations (continued) Null = V 7 in sectors 1, 3, 5 Null = V 0 in sectors 2, 4, 6 Null = V 0 in sectors 1, 3, 5 Null = V 7 in sectors 2, 4, 6 1 1 0. 8 0. 6 0. 4 0. 2 0 0 0 60 120 180 240 300 360 Kappa TM Electronics A B C 1 0. 8 Null = alt-rev (null alternates every sequence and sequence reverses. ) Most popular form of SVM 0. 6 • Similar waveforms to Third Harmonic 0. 4 0. 2 0 0 60 A 120 180 240 B Keeping your motors spinning. 300 360 C Dave Wilson

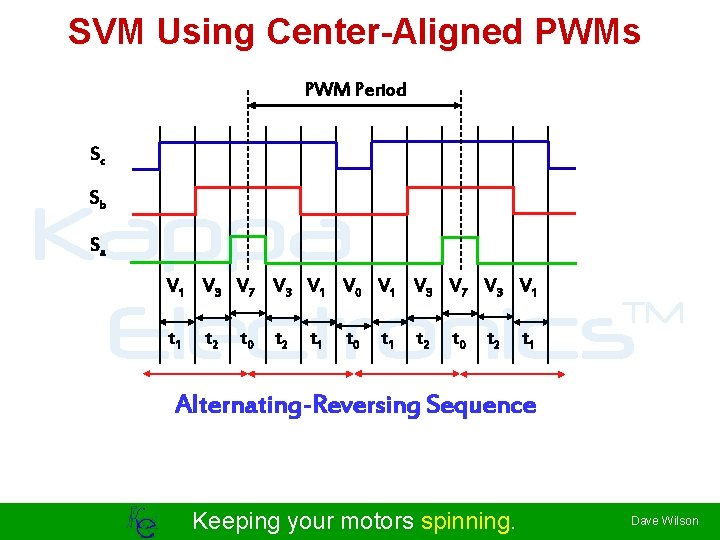
SVM Using Center-Aligned PWMs PWM Period Sc Sb Kappa TM Electronics Sa V 1 V 3 V 7 V 3 V 1 V 0 V 1 V 3 V 7 V 3 V 1 t 2 t 0 t 2 t 1 t 0 t 1 t 2 t 0 t 2 t 1 Alternating-Reversing Sequence Keeping your motors spinning. Dave Wilson

SVM with PWMs Procedure for implementing SVM with Center-Aligned PWM Module 1 Check which sector the Vref vector is in. (5 compares) 2 Calculate T 1, T 2, and T 0 from block below. (3 multiples) 3 Adjust PWMs High times based on table below. (1 -3 additions) T 1 = T • m • SIN(60 - ) T 2 = T • m • SIN( ) T 0 = T - T 1 - T 2 V 0 in 1, 3, 5 V 7 in 2, 4, 6 Alternating Reversing Sequencing Null = V 0 Null = V 7 in 1, 3, 5 V 0 in 2, 4, 6 U = T 1+T 2 Sector 1 V = T 2 W=0 U = 100% V = T 0+T 2 W = T 0 U = T 1+T 2 V = T 2 W=0 U = T 1+T 2+. 5 T 0 V = T 2+. 5 T 0 W =. 5 T 0 U = T 1 Sector 2 V = T 1+T 2 W=0 U = T 0+T 1 V = 100% W = T 0 U = T 1+. 5 T 0 V = T 1+T 2+. 5 T 0 W =. 5 T 0 U=0 Sector 3 V = T 1+T 2 W = T 2 U = T 0 V = 100% W = T 0+T 2 U=0 V = T 1+T 2 W = T 2 U =. 5 T 0 V = T 1+T 2+. 5 T 0 W = T 2+. 5 T 0 U=0 Sector 4 V = T 1 W = T 1+T 2 U = T 0 V = T 0+T 1 W = 100% U=0 V = T 1 W = T 1+T 2 U = T 0 V = T 0+T 1 W = 100% U =. 5 T 0 V = T 1+. 5 T 0 W = T 1+T 2+. 5 T 0 U = T 2 Sector 5 V = 0 W = T 1+T 2 U = T 0+T 2 V = T 0 W = 100% U = T 2 V=0 W = T 1+T 2 U = T 2+. 5 T 0 V =. 5 T 0 W = T 1+T 2+. 5 T 0 U = T 1+T 2 Sector 6 V = 0 W = T 1 U = 100% V = T 0 W = T 0+T 1 U = T 1+T 2 V=0 W = T 1 U = 100% V = T 0 W = T 0+T 1 U = T 1+T 2+. 5 T 0 V =. 5 T 0 W = T 1+. 5 T 0 Kappa TM Electronics Note: All calculations referenced to top switch Source: Understanding Space Vector Modulation, by Peter Pinewski, EDN Products Edition, March 7, 1996 Keeping your motors spinning. Dave Wilson

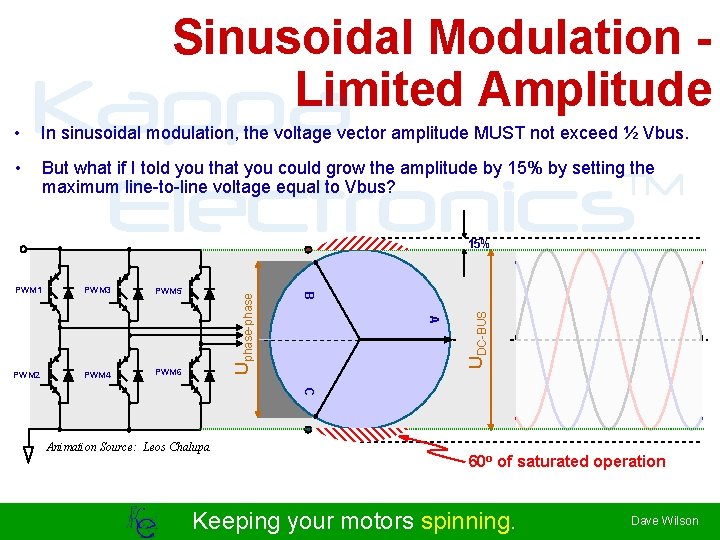
Sinusoidal Modulation Limited Amplitude • • Kappa TM Electronics In sinusoidal modulation, the voltage vector amplitude MUST not exceed ½ Vbus. But what if I told you that you could grow the amplitude by 15% by setting the maximum line-to-line voltage equal to Vbus? PWM 2 PWM 4 PWM 6 UDC-BUS PWM 5 A PWM 3 B PWM 1 Uphase-phase 15% C Animation Source: Leos Chalupa 60 o of saturated operation Keeping your motors spinning. Dave Wilson

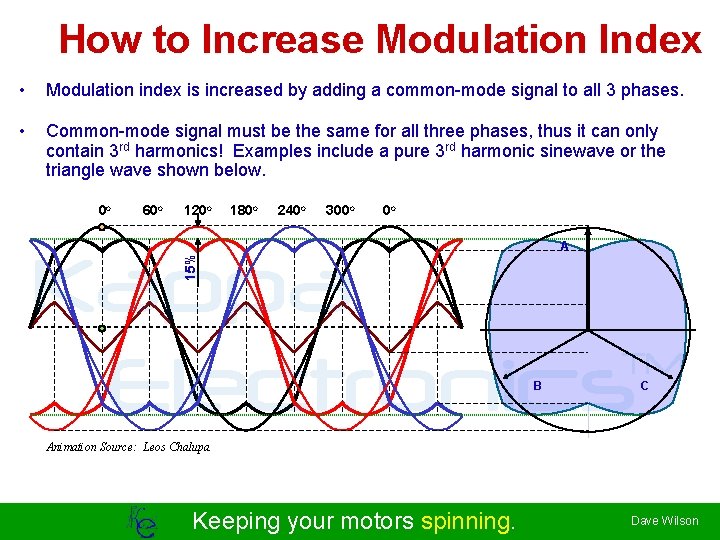
How to Increase Modulation Index • Modulation index is increased by adding a common-mode signal to all 3 phases. • Common-mode signal must be the same for all three phases, thus it can only contain 3 rd harmonics! Examples include a pure 3 rd harmonic sinewave or the triangle wave shown below. 0 o 60 o 120 o 180 o 240 o 300 o 0 o A 15% Kappa TM Electronics B C Animation Source: Leos Chalupa Keeping your motors spinning. Dave Wilson

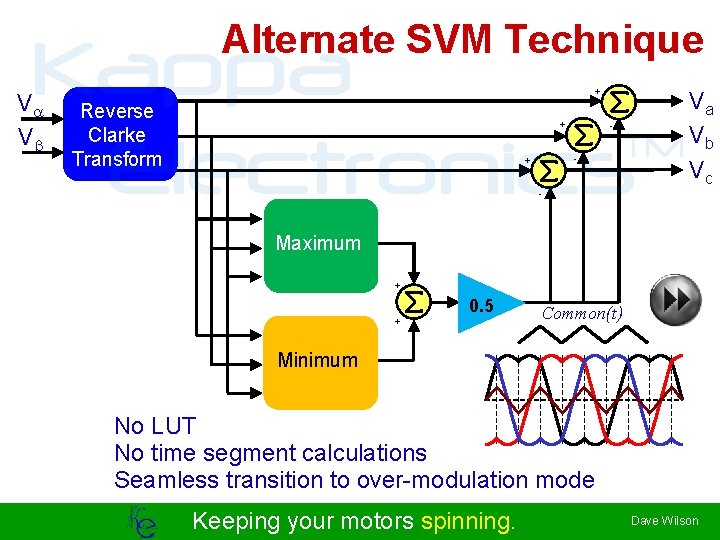
Alternate SVM Technique Kappa TM Electronics V Vb + Reverse Clarke Transform + - - + Va Vb Vc - Maximum + + 0. 5 Common(t) Minimum No LUT No time segment calculations Seamless transition to over-modulation mode Keeping your motors spinning. Dave Wilson

Field Weakening Kappa TM Electronics applied voltage At high speeds, the back-EMF amplitude is high, which impedes the ability of the applied voltage to develop current. Keeping your motors spinning. Dave Wilson

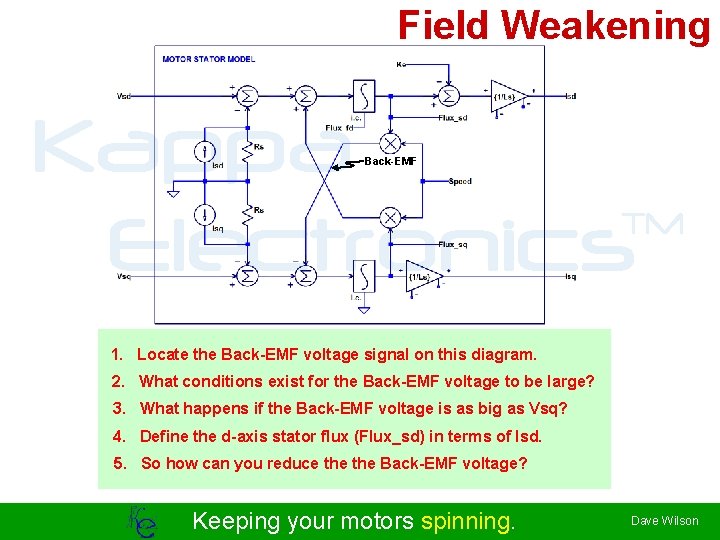
Field Weakening Kappa TM Electronics Back-EMF 1. Locate the Back-EMF voltage signal on this diagram. 2. What conditions exist for the Back-EMF voltage to be large? 3. What happens if the Back-EMF voltage is as big as Vsq? 4. Define the d-axis stator flux (Flux_sd) in terms of Isd. 5. So how can you reduce the Back-EMF voltage? Keeping your motors spinning. Dave Wilson

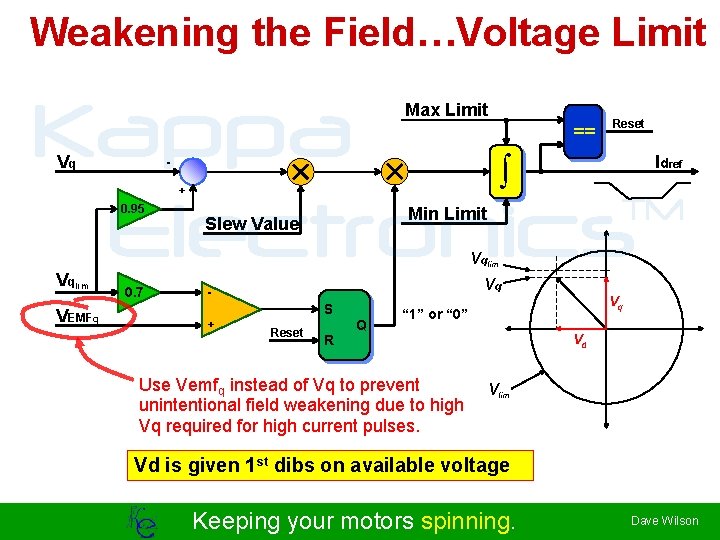
Weakening the Field…Voltage Limit Kappa ò TM Electronics Max Limit == Vq Reset Idref - + 0. 95 Min Limit Slew Value Vqlim VEMFq 0. 7 Vq S + Reset R Q Vq “ 1” or “ 0” Use Vemfq instead of Vq to prevent unintentional field weakening due to high Vq required for high current pulses. Vd Vlim Vd is given 1 st dibs on available voltage Keeping your motors spinning. Dave Wilson

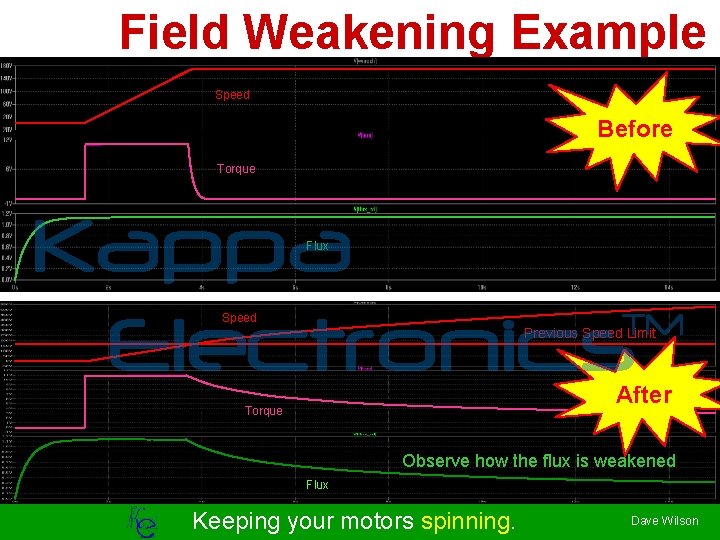
Field Weakening Example Speed Before Torque Kappa TM Electronics Flux Speed Previous Speed Limit After Torque Observe how the flux is weakened Flux Keeping your motors spinning. Dave Wilson