2015 Scientific Computing Intro to Linear Classifiers Definition

2015 Scientific Computing Intro to Linear Classifiers Definition The output is based on linear combination of features Types Linear perceptrons SVM (support vector machine) 2 2022/1/3 2

2015 Scientific Computing ADALINE (Adaptive Linear Neuron) network and its learning rule, LMS (Least Mean Square) algorithm are proposed by Widrow and Marcian Hoff in 1960. Both ADALINE network and the perceptron suffer from the same inherent limitation: they can only solve linearly separable problems. The LMS algorithm minimizes mean square error (MSE 3 2022/1/3 3

2015 Scientific Computing Example: Gender Classification Goal Determine a person’s gender from his/her profile data Features collected 4 2022/1/3 • • • Birthday Blood type Height and weight Density Three measures Hair length Voice pitch … Chromosome 4

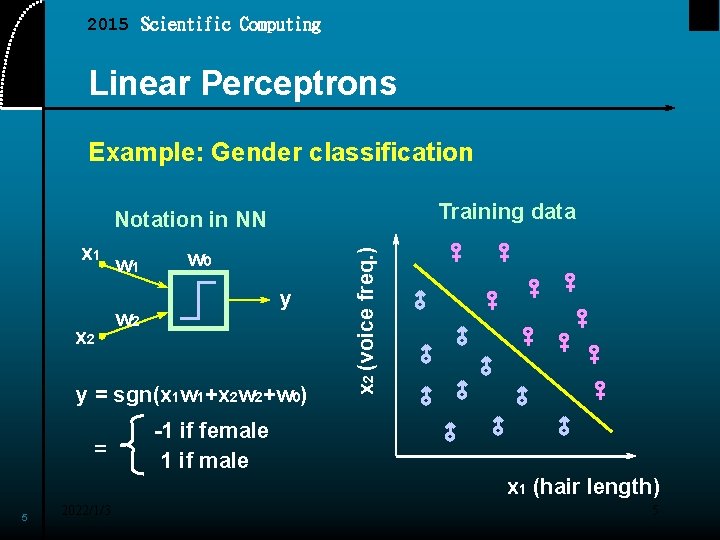
2015 Scientific Computing Linear Perceptrons Example: Gender classification Training data x 1 x 2 w 1 w 0 y w 2 y = sgn(x 1 w 1+x 2 w 2+w 0) = x 2 (voice freq. ) Notation in NN -1 if female 1 if male x 1 (hair length) 5 2022/1/3 5

2015 Scientific Computing Learning Rule of Linear Perceptrons Example: Gender classification Training data x 1 x 2 w 1 w 0 y w 2 y = sgn(x 1 w 1+x 2 w 2+w 0) = x 2 (voice freq. ) Notation in NN -1 if female 1 if male x 1 (hair length) 6 2022/1/3 6

2015 Scientific Computing Characteristics of LC Characteristics: • Guaranteed to converge to a set of weights that will perfectly classify all the data if such a solution exists • Data rescaling is necessary to speed up convergence of the algorithm • Stops whenever a solution with zero error rate is found • Nonlinear decision boundaries can also be found by the adaptive technique • For a k-class problem, it needs k(k-1)/2 decision boundaries to do complete classification 7 2022/1/3 7

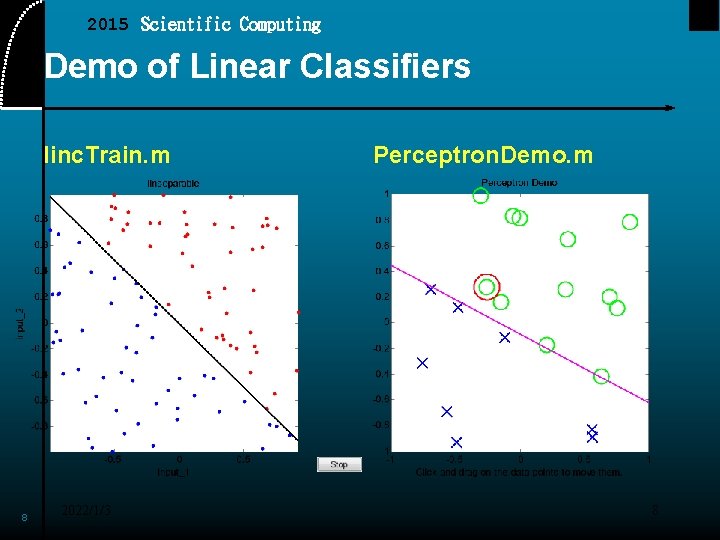
2015 Scientific Computing Demo of Linear Classifiers linc. Train. m 8 2022/1/3 Perceptron. Demo. m 8