2011 Pearson Education Inc Statistics for Business and

Statistics for Business and Economics Chapter 9 Categorical Data Analysis © 2011 Pearson Education,

Contents 9. 1 Categorical Data and the Multinomial Experiment 9. 2 Testing Category Probabilities: One-Way Table 9. 3 Testing Category Probabilities: Two-Way Contingency Table 9. 4 A Word of Caution about Chi-Square Tests © 2011 Pearson Education, Inc

Learning Objectives 1. Discuss qualitative (i. e. , categorical) data with more than two outcomes 2. Present a chi-square hypothesis test for comparing the category proportions associated with a single qualitative variable– called a one-way analysis 3. Present a chi-square hypothesis test for relating two qualitative variables–called a two-way analysis © 2011 Pearson Education, Inc

9. 1 Categorical Data and Multinomial Experiment © 2011 Pearson Education, Inc

Qualitative Data • Qualitative random variables yield responses that can be classified – Example: gender (male, female) • Qualitative data that fall in more than two categories often result from a multinomial experiment © 2011 Pearson Education, Inc

Properties of the Multinomial Experiment 1. The experiment consists of n identical trials. 2. There are k possible outcomes to each trial. These outcomes are called classes, categories, or cells. 3. The probabilities of the k outcomes, denoted by p 1, p 2, …, pk, remain the same from trial to trial, where p 1 + p 2 + … + pk = 1. 4. The trials are independent. 5. The random variables of interest are the cell counts, n 1, n 2, …, nk, of the number of observations that fall in each of the k classes. © 2011 Pearson Education, Inc

9. 2 Testing Category Probabilities: One-Way Table © 2011 Pearson Education, Inc

Multinomial Experiment In this section, we consider a multinomial experiment with k outcomes that correspond to categories of a single qualitative variable. The results of such an experiment are summarized in a one-way table. The term one-way is used because only one variable is classified. Typically, we want to make inferences about the true proportions that occur in the k categories based on the sample information in the one-way table. © 2011 Pearson Education, Inc

Chi-Square ( Test for k Proportions 2) • Tests equality (=) of proportions only – Example: p 1 =. 2, p 2=. 3, p 3 =. 5 • One variable with several levels • Uses one-way contingency table © 2011 Pearson Education, Inc

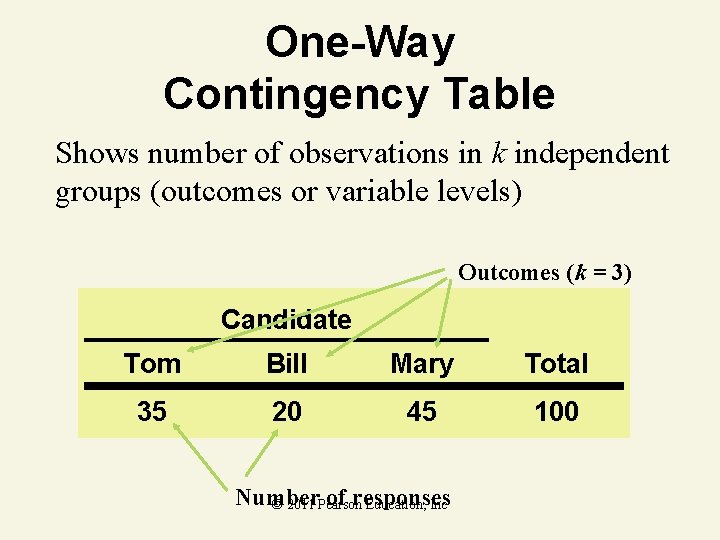
One-Way Contingency Table Shows number of observations in k independent groups (outcomes or variable levels) Outcomes (k = 3) Candidate Tom Bill Mary Total 35 20 45 100 Number of responses © 2011 Pearson Education, Inc

A Test of a Hypothesis about Multinomial Probabilities: One-Way Table H 0: p 1 = p 1, 0, p 2 = p 2, 0, …, pk = pk, 0 where p 1, 0, p 2, 0, …, pk, 0 represent the hypothesized values of the multinomial probabilities. Ha: At least one of the multinomial probabilities does not equal its hypothesized value. © 2011 Pearson Education, Inc

A Test of a Hypothesis about Multinomial Probabilities: One-Way Table where Ei = npi, 0 is the expected cell count–that is, the expected number of outcomes of type i assuming that H 0 is true. The total sample size is n. where has (k – 1) df. © 2011 Pearson Education, Inc

Conditions Required for a Valid Test: One-way Table 1. A multinomial experiment has been conducted. This is generally satisfied by taking a random sample from the population of interest. 2. The sample size n is large. This is satisfied if for every cell, the expected cell count Ei will be equal to 5 or more. © 2011 Pearson Education, Inc

2 Test Basic Idea 1. Compares observed count to expected count assuming null hypothesis is true 2. Closer observed count is to expected count, the more likely the H 0 is true • Measured by squared difference relative to expected count — Reject large values © 2011 Pearson Education, Inc

Finding Critical Value Example What is the critical 2 value if k = 3, and =. 05? If ni = E(ni), 2 = 0. Do not reject H 0 Reject H 0 =. 05 df = k - 1 = 2 0 2 Table (Portion) DF. 995 1. . . 2 0. 010 5. 991 2 Upper Tail Area …. 95 … … 0. 004 … … 0. 103 … © 2011 Pearson Education, Inc . 05 3. 841 5. 991

2 Test for k Proportions Example As personnel director, you want to test the perception of fairness of three methods of performance evaluation. Of 180 employees, 63 rated Method 1 as fair, 45 rated Method 2 as fair, 72 rated Method 3 as fair. At the. 05 level of significance, is there a difference in perceptions? © 2011 Pearson Education, Inc

2 • • • Test for k Proportions Solution H 0: p 1 = p 2 = p 3 = 1/3 Ha: At least 1 is different =. 05 n 1 = 63 n 245 = n 3 = 72 Critical Value(s): Reject H 0 =. 05 0 5. 991 © 2 2011 Pearson Education, Inc

2 Test for k Proportions Solution © 2011 Pearson Education, Inc

2 • • • Test for k Proportions Solution H 0: p 1 = p 2 = p 3 = 1/3 Test Statistic: 2 = 6. 3 Ha: At least 1 is different =. 05 n 1 = 63 n 245 = n 3 = 72 Critical Value(s): Decision: Reject H 0 Reject at =. 05 Conclusion: There is evidence of a © 2 2011 Pearson Education, difference in proportions Inc =. 05 0 5. 991

9. 3 Testing Category Probabilities: Two-Way (Contingency) Table © 2011 Pearson Education, Inc

2 Test of Independence • Shows if a relationship exists between two qualitative

2 Test of Independence Contingency Table Shows number of observations from one sample

Finding Expected Cell Counts for a Two-Way Contingency Table The estimate of the expected number of observations falling into the cell in row i and column j is given by where Ri = total for row i, Cj = total for column j, and n = sample size. © 2011 Pearson Education, Inc

General Form of a Contingency Table Analysis: 2 -Test for Independence H 0: The two classifications are independent. Ha: The two classifications are dependent. where Rejection region: where has (r – 1)(c – 1)© 2011 df. Pearson Education, Inc

Conditions Required for a Valid 2 -Test: Contingency Table 1. A multinomial experiment has been conducted. We may then consider this to be a multinomial experiment with r c possible outcomes. 2. The sample size n is large. This is satisfied if for every cell, the expected count Ei will be equal to 5 or more. © 2011 Pearson Education, Inc

Test of Independence 2 Expected Counts 1. Statistical independence means joint probability equals product of marginal probabilities 2. Compute marginal probabilities and multiply for joint probability 3. Expected count is sample size times joint probability © 2011 Pearson Education, Inc

Expected Count Example Marginal probability = 112 160 House Style Location Urban Rural Obs. Total Split–Level 63 49 112 Ranch 15 33 48 Total 78 82 160 Marginal probability = 78 160 © 2011 Pearson Education, Inc

Expected Count Example Joint probability = House Style 112 78 160 Marginal probability = 112 160 Location Urban Rural Obs. Total Split–Level 63 49 112 Ranch 15 33 48 Total 78 82 160 112 78 78 Expected count = 160· Marginal probability = 160 160 © 2011 Pearson Education, Inc = 54. 6

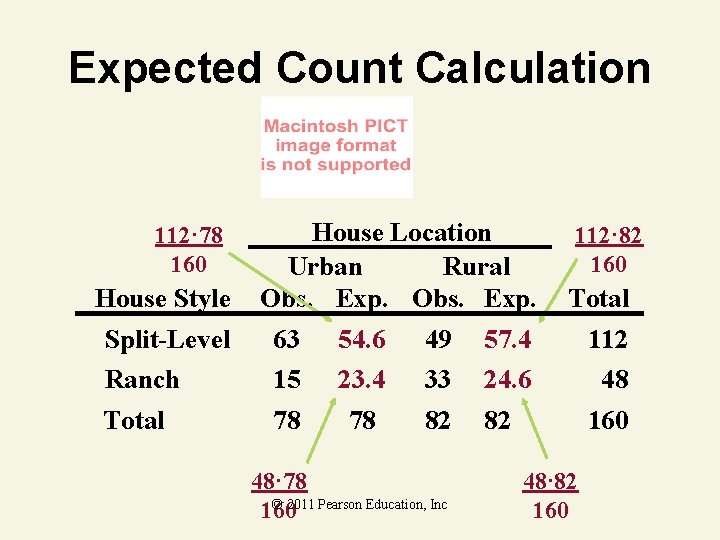
Expected Count Calculation 112· 78 160 House Style House Location Urban Rural Obs. Exp. 112· 82 160 Total Split-Level 63 54. 6 49 57. 4 112 Ranch 15 23. 4 33 24. 6 48 Total 78 78 82 82 48· 78 © 2011 Pearson Education, Inc 160 48· 82 160

2 Test of Independence Example As a realtor you want to determine if house style and house location are related. At the. 05 level of significance, is there evidence of a relationship? © 2011 Pearson Education, Inc

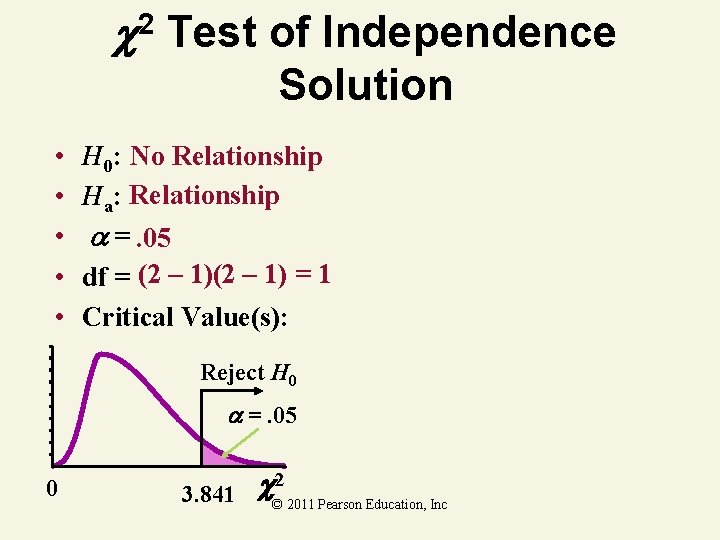
2 Test of Independence Solution • • • H 0: No Relationship Ha: Relationship =. 05 df = (2 – 1) = 1 Critical Value(s): Reject H 0 =. 05 0 3. 841 © 2 2011 Pearson Education, Inc

2 Test of Independence Solution Eij 5 in all cells 112· 78 160

2 Test of Independence Solution © 2011 Pearson Education, Inc

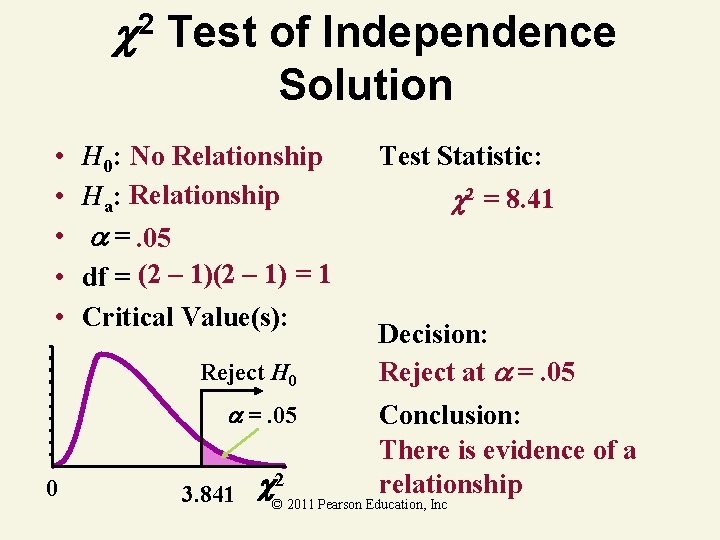
2 Test of Independence Solution • • • H 0: No Relationship Ha: Relationship =. 05 df = (2 – 1) = 1 Critical Value(s): Reject H 0 =. 05 0 3. 841 Test Statistic: 2 = 8. 41 Decision: Reject at =. 05 Conclusion: There is evidence of a relationship © 2 2011 Pearson Education, Inc

2 Test of Independence Thinking Challenge You’re a marketing research analyst. You ask a random sample of 286 consumers if they purchase Diet Pepsi or Diet Coke. At the. 05 level of significance, is there evidence of a relationship? Diet Coke No Yes Total Diet Pepsi No Yes 84 32 48 122 132 154 © 2011 Pearson Education, Inc Total 116 170 286

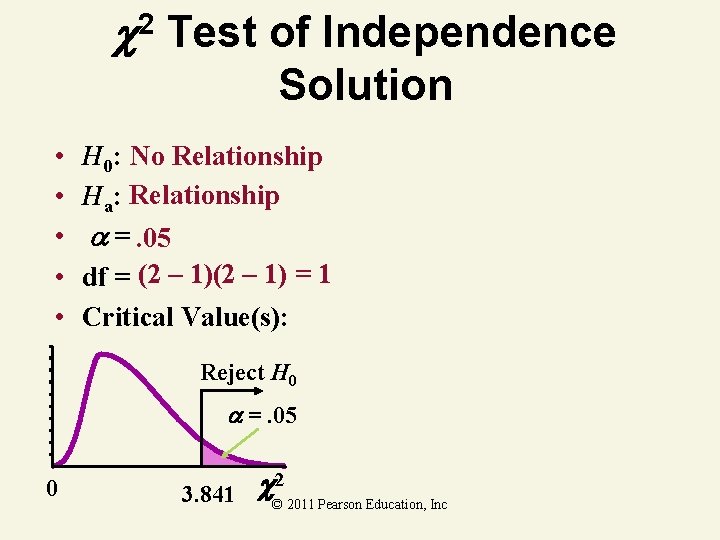
2 Test of Independence Solution • • • H 0: No Relationship Ha: Relationship =. 05 df = (2 – 1) = 1 Critical Value(s): Reject H 0 =. 05 0 3. 841 © 2 2011 Pearson Education, Inc

2 Test of Independence Solution* Eij 5 in all cells 116· 132 286

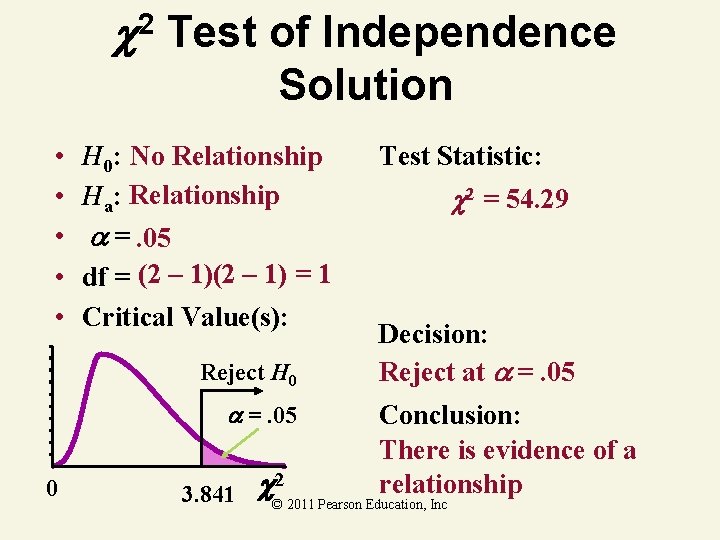
2 Test of Independence Solution • • • H 0: No Relationship Ha: Relationship =. 05 df = (2 – 1) = 1 Critical Value(s): Reject H 0 =. 05 0 3. 841 Test Statistic: 2 = 54. 29 Decision: Reject at =. 05 Conclusion: There is evidence of a relationship © 2 2011 Pearson Education, Inc

2 Test of Independence Thinking Challenge 2 There is a statistically significant relationship between purchasing Diet Coke and Diet Pepsi. So what do you think the relationship is? Aren’t they competitors? Diet Coke No Yes Total Diet Pepsi No Yes 84 32 48 122 132 154 © 2011 Pearson Education, Inc Total 116 170 286

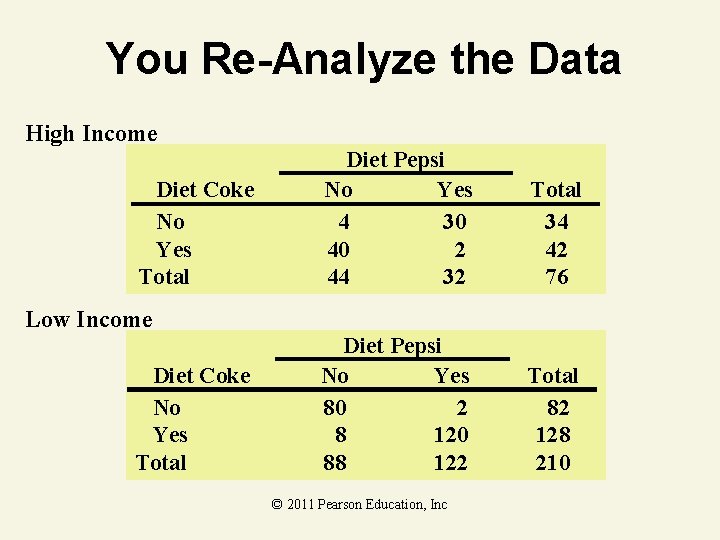
You Re-Analyze the Data High Income Diet Coke No Yes Total Diet Pepsi No Yes 4 30 40 2 44 32 Total 34 42 76 Diet Pepsi No Yes 80 2 8 120 88 122 Total 82 128 210 Low Income Diet Coke No Yes Total © 2011 Pearson Education, Inc

True Relationships Diet Coke Underlying causal relation Control or intervening variable (true cause) Apparent

Moral of the Story Numbers don’t think - People do! © 2011 Pearson Education,

9. 4 A Word of Caution about Chi-Square Tests © 2011 Pearson Education, Inc

Caution about the 2 Test The 2 is one of the most widely applied statistical tools and also one of the most abused statistical tool. Be certain the experiment satisfies the assumptions. Be certain the sample is drawn from the correct population. Avoid using when the expected counts are very small. © 2011 Pearson Education, Inc

Caution about the 2 Test • If the 2 value does not exceed the established critical value of 2 , do not accept the hypothesis of independence. You risk a Type II error. Avoid concluding that two classifications are independent, even when 2 is small. • If a contingency table 2 value does exceed the critical value, we must be careful to avoid inferring that a causal relationship exists between the classifications. The existence of a causal relationship cannot be established by a contingency table analysis. © 2011 Pearson Education, Inc

Key Ideas Multinomial Data Qualitative data that fall into more than two categories (or

Key Ideas Properties of a Multinomial Experiment 1. n identical trials 2. k possible outcomes 3. probabilities of the k outcomes (p 1, p 2, …, pk) remain the same from trial to trial, where p 1 + p 2 + … + pk = 1 4. trials are independent 5. variables of interest: cell counts (i. e. , number of observations falling into each outcome category), denoted n 1, n 2, …, nk © 2011 Pearson Education, Inc

Key Ideas One-Way Table Summary table for a single qualitative variable Two-Way (Contingency) Table

Key Ideas Chi-Square ( 2) Statistic used to test category probabilities in one-way and two-way tables Chi-Square tests for independence should not be used to infer a causal relationship between 2 Qualitative Variables © 2011 Pearson Education, Inc