2011 Pearson Education Inc Statistics for Business and

Statistics for Business and Economics Chapter 7 Inferences Based on Two Samples: Confidence Intervals

Content 1. Identifying the Target Parameter 2. Comparing Two Population Means: Independent Sampling 3. Comparing Two Population Means: Paired Difference Experiments 4. Comparing Two Population Proportions: Independent Sampling 5. Determining the Sample Size 6. Comparing Two Population Variances: Independent Sampling © 2011 Pearson Education, Inc

Learning Objectives 1. Learn how to compare two populations using confidence intervals and tests of hypotheses 2. Apply these inferential methods to problems where we want to compare • Two population means • Two population proportions • Two population variances © 2011 Pearson Education, Inc

Learning Objectives 3. Determine the sizes of the samples necessary to estimate the difference

7. 1 Identifying the Target Parameter © 2011 Pearson Education, Inc

Thinking Challenge How would you try to answer these questions? • Who gets higher

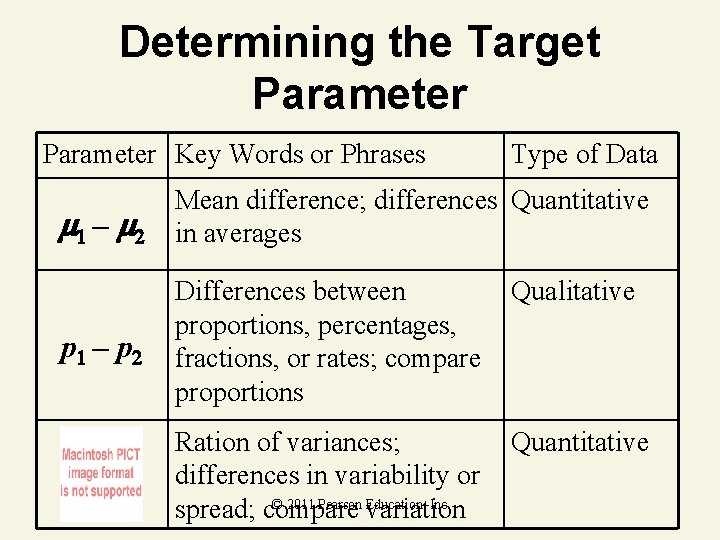
Determining the Target Parameter Key Words or Phrases Type of Data 1 – 2 Mean difference; differences Quantitative in averages Qualitative p 1 – p 2 Differences between proportions, percentages, fractions, or rates; compare proportions Ration of variances; differences in variability or © 2011 Pearson Education, Inc spread; compare variation Quantitative

7. 2 Comparing Two Population Means: Independent Sampling © 2011 Pearson Education, Inc

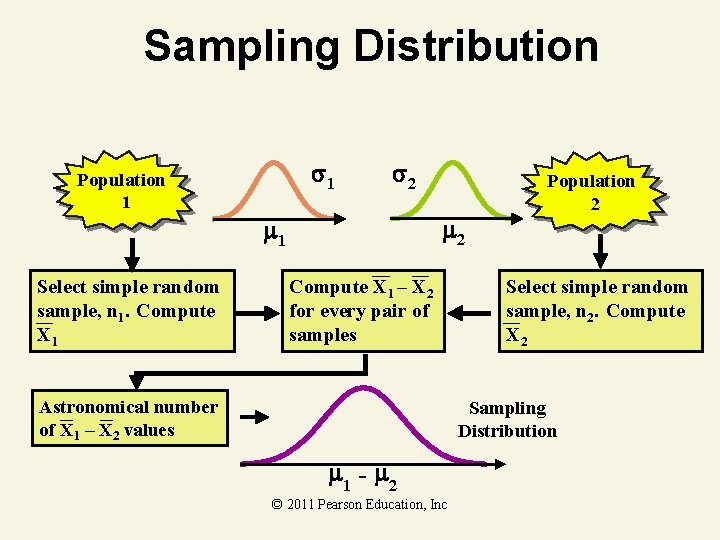
Sampling Distribution 1 Population 1 2 2 1 Select simple random sample, n 1. Compute X 1 – X 2 for every pair of samples Astronomical number of X 1 – X 2 values Population 2 Select simple random sample, n 2. Compute X 2 Sampling Distribution 1 - 2 © 2011 Pearson Education, Inc

Large-Sample Confidence Interval for (μ 1 – μ 2) © 2011 Pearson Education, Inc

Large-Sample Test of Hypothesis for (µ 1 – µ 2) One-Tailed Test H 0: (µ 1 – µ 2) = D 0 Ha: (µ 1 – µ 2) < D 0 [or Ha: (µ 1 – µ 2) > D 0 ] where D 0 = Hypothesized difference between the means (the difference is often hypothesized to be equal to 0) Test statistic: Rejection region: z < –z [or z > z when Ha: (µ 1 – µ 2) > D 0 ] © 2011 Pearson Education, Inc

Large-Sample Test of Hypothesis for (µ 1 – µ 2) Two-Tailed Test H 0: (µ 1 – µ 2) = D 0 Ha: (µ 1 – µ 2) ≠ D 0 where D 0 = Hypothesized difference between the means (the difference is often hypothesized to be equal to 0) Test statistic: Rejection region: |z| > z © 2011 Pearson Education, Inc

Conditions Required for Valid Large-Sample Inferences about (μ 1 – μ 2) 1. The two samples are randomly selected in an independent manner from the two target populations. 2. The sample sizes, n 1 and n 2, are both large (i. e. , n 1 ≥ 30 and n 2 ≥ 30). [Due to the Central Limit Theorem, this condition guarantees that the sampling distribution of will be approximately normal regardless of the shapes of the underlying probability distributions of the populations. Also, and will provide good approximations to and when the samples are both large. ] © 2011 Pearson Education, Inc

Large-Sample Confidence Interval Example You’re a financial analyst for Charles Schwab. You want to estimate the difference in dividend yield between stocks listed on NYSE and NASDAQ. You collect the following data: NYSE NASDAQ Number 121 125 Mean 3. 27 2. 53 Std Dev 1. 30 1. 16 What is the 95% confidence interval for the difference between the mean dividend yields? © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Large-Sample Confidence Interval Solution © 2011 Pearson Education, Inc

Hypotheses for Means of Two Independent Populations Research Questions Hypothesis No Difference Any Difference Pop 1 ³ Pop 2 Pop 1 £ Pop 2 Pop 1 < Pop 2 Pop 1 > Pop 2 H 0 Ha © 2011 Pearson Education, Inc

Large-Sample Test Example You’re a financial analyst for Charles Schwab. You want to find out if there is a difference in dividend yield between stocks listed on NYSE and NASDAQ. You collect the following data: NYSE NASDAQ Number 121 125 Mean 3. 27 2. 53 Std Dev 1. 30 1. 16 Is there a difference in average yield ( =. 05)? © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Large-Sample Test Solution • • • H 0: 1 - 2 = 0 ( 1 = 2) Ha: 1 - 2 0 ( 1 2) . 05 n 1= 121 , n 2 = 125 Critical Value(s): Reject H 0 . 025 -1. 96 0 1. 96 . 025 Test Statistic: Decision: Reject at =. 05 Conclusion: There is evidence of a z difference in means © 2011 Pearson Education, Inc

Large-Sample Test Thinking Challenge You’re an economist for the Department of Education. You want to find out if there is a difference in spending per pupil between urban and rural high schools. You collect the following: Urban Rural Number 35 35 Mean $ 6, 012 $ 5, 832 Std Dev $ 602 $ 497 Is there any difference in population means ( =. 10)? © 2011 Pearson Education, Inc

Large-Sample Test Solution* • • • H 0: 1 - 2 = 0 ( 1 = 2) Ha: 1 - 2 0 ( 1 2) . 10 n 1 = 35, n 2 = 35 Critical Value(s): Reject H 0 . 05 -1. 645 Reject H 0 . 05 0 1. 645 Test Statistic: Decision: Do not reject at =. 10 Conclusion: There is no evidence of a z difference in means © 2011 Pearson Education, Inc

Small-Sample Confidence Interval for (μ 1 – μ 2) (Independent Samples) where and ta/2

Small-Sample Test of Hypothesis for (µ 1 – µ 2) One-Tailed Test H 0: (µ 1 – µ 2) = D 0 Ha: (µ 1 – µ 2) < D 0 [or Ha: (µ 1 – µ 2) > D 0 ] Test statistic: Rejection region: t < –t [or t > t when Ha: (µ 1 – µ 2) > D 0 ] where t is based on (n 1 + n 2 – 2) degrees of freedom. © 2011 Pearson Education, Inc

Small-Sample Test of Hypothesis for (µ 1 – µ 2) Two-Tailed Test H 0: (µ 1 – µ 2) = D 0 Ha: (µ 1 – µ 2) ≠ D 0 Test statistic: Rejection region: |t| > t /2 where ta/2 is based on© 2011 (n 1 Pearson + n 2 Education, – 2) Inc degrees of freedom.

Conditions Required for Valid Small-Sample Inferences about (μ 1 – μ 2) 1. The two samples are randomly selected in an independent manner from the two target populations. 2. Both sampled populations have distributions that are approximately equal. 3. The populations variances are equal (i. e. , ). © 2011 Pearson Education, Inc

Small-Sample Confidence Interval Example You’re a financial analyst for Charles Schwab. You want to estimate the difference in dividend yield between stocks listed on the NYSE and NASDAQ. You collect the following data: NYSE NASDAQ Number 11 15 Mean 3. 27 2. 53 Std Dev 1. 30 1. 16 Assuming normal populations, what is the 95% confidence interval for the difference between the mean dividend yields? © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Small-Sample Confidence Interval Solution df = n 1 + n 2 – 2 =

Small-Sample Test Example You’re a financial analyst for Charles Schwab. Is there a difference in dividend yield between stocks listed on the NYSE and NASDAQ? You collect the following data: NYSE NASDAQ Number 11 15 Mean 3. 27 2. 53 Std Dev 1. 30 1. 16 Assuming normal populations, And population variances are equal is there a difference in average yield ( =. 05)? © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Small-Sample Test Solution • • • H 0: 1 – 2 = 0 (

Small-Sample Test Solution © 2011 Pearson Education, Inc

Small-Sample Test Solution H 0: 1 – 2 = 0 ( 1 = 2) Test Statistic: Ha: 1 – 2 0 ( 1 2) . 05 df 11 + 15 – 2 = 24 Critical Value(s): Decision: Do not reject at =. 05 Reject H 0 • • • . 025 -2. 064 . 025 0 2. 064 t Conclusion: There is no evidence of a difference in means © 2011 Pearson Education, Inc

Small-Sample Test Thinking Challenge You’re a research analyst for General Motors. Assuming equal variances, is there a difference in the average miles per gallon (mpg) of two car models ( =. 05)? You collect the following: Sedan Van Number 15 11 Mean 22. 00 20. 27 Std Dev 4. 77 3. 64 © 2011 Pearson Education, Inc

Small-Sample Test Solution* H 0: 1 – 2 = 0 ( 1 = 2) Test Statistic: Ha: 1 – 2 0 ( 1 2) . 05 df 15 + 11 – 2 = 24 Critical Value(s): Decision: Do not reject at =. 05 Reject H 0 • • • . 025 -2. 064 . 025 0 2. 064 t Conclusion: There is no evidence of a difference in means © 2011 Pearson Education, Inc

Approximate Small-Sample Procedures when 1. Equal sample sizes (n 1 = n 2 = n) Confidence interval: Test statistic H 0: where t is based on v = n 1 + n 2 – 2 = 2(n – 1) degrees of freedom. © 2011 Pearson Education, Inc

Approximate Small-Sample Procedures when 2. Unequal sample sizes (n 1 ≠ n 2) Confidence

Approximate Small-Sample Procedures when Note: The value of v will generally not be an

What Should You Do if the Assumptions Are Not Satisfied? If you are concerned that the assumptions are not satisfied, use the Wilcoxon rank sum test for independent samples to test for a shift in population distributions. See Chapter 14. © 2011 Pearson Education, Inc

7. 3 Comparing Two Population Means: Paired Difference Experiments © 2011 Pearson Education, Inc

Paired-Difference Test of Hypothesis for µd = (µ 1 – µ 2) One-Tailed Test H 0: µd = D 0 Ha: µd < D 0 [or Ha: µd > D 0 ] Large Sample Test statistic: Rejection region: z < –z [or z > z when Ha: (µd > D 0 ] © 2011 Pearson Education, Inc

Paired-Difference Test of Hypothesis for µd = (µ 1 – µ 2) One-Tailed Test H 0: µd = D 0 Ha: µd < D 0 [or Ha: µd > D 0 ] Small Sample Test statistic: Rejection region: t < –t [or t > t when Ha: (µd > D 0 ] where t is based on (nd – 1) degrees of freedom. © 2011 Pearson Education, Inc

Paired-Difference Test of Hypothesis for µd = (µ 1 – µ 2) Two-Tailed Test H 0: µd = D 0 Ha : µd ≠ D 0 Small Sample Test statistic: Rejection region: |t| > t where t is based on (nd – 1) degrees of freedom. © 2011 Pearson Education, Inc

Paired-Difference Confidence Interval for µd = (µ 1 – µ 2) Large Sample Small

Conditions Required for Valid Large-Sample Inferences about µd 1. A random sample of differences is selected from the target population of differences. 2. The sample size nd is large (i. e. , nd ≥ 30); due to the Central Limit Theorem, this condition guarantees that the test statistic will be approximately normal regardless of the shape of the underlying probability distribution of the population. © 2011 Pearson Education, Inc

Conditions Required for Valid Small-Sample Inferences about µd 1. A random sample of differences is selected from the target population of differences. 2. The population of differences has a distribution that is approximately normal. © 2011 Pearson Education, Inc

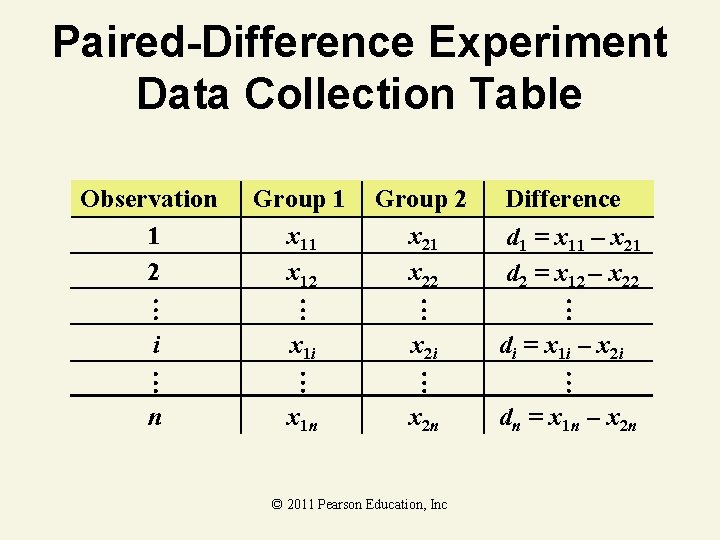
Paired-Difference Experiment Data Collection Table Observation 1 2 Group 1 x 12 Group 2 x 21 x 22 Difference d 1 = x 11 – x 21 d 2 = x 12 – x 22 i x 1 i x 2 i n x 1 n x 2 n © 2011 Pearson Education, Inc di = x 1 i – x 2 i dn = x 1 n – x 2 n

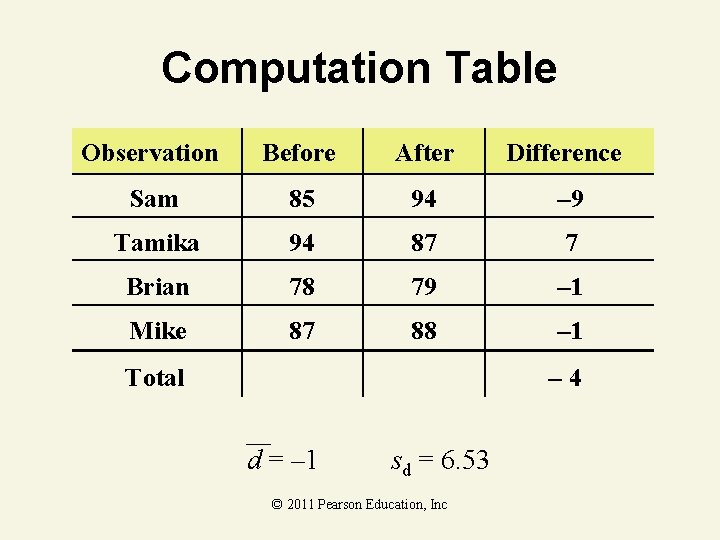
Paired-Difference Experiment Confidence Interval Example You work in Human Resources. You want to see if there is a difference in test scores after a training program. You collect the following test score data: Name Before (1) After (2) Sam 85 94 Tamika 94 87 Brian 78 79 Mike 87 88 Find a 90% confidence interval for the mean difference in test scores. © 2011 Pearson Education, Inc

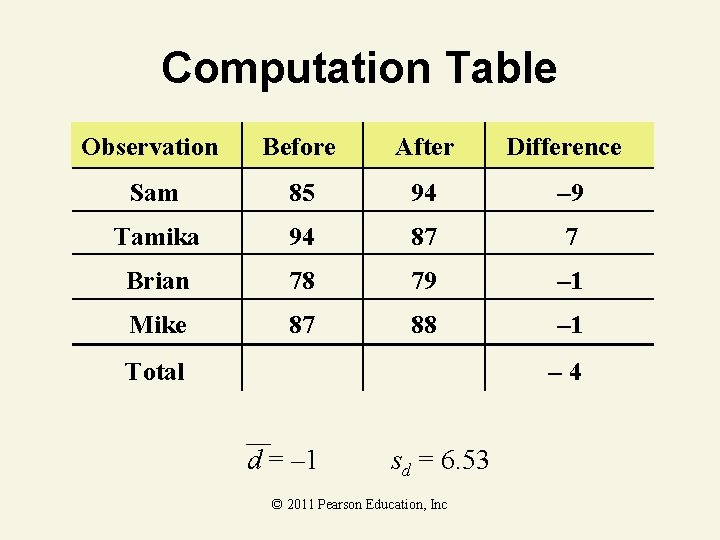
Computation Table Observation Before After Difference Sam 85 94 – 9 Tamika 94 87

Paired-Difference Experiment Confidence Interval Solution df = nd – 1 = 4 – 1

Hypotheses for Paired. Difference Experiment Research Questions Hypothesis No Difference Any Difference Pop 1 ³ Pop 2 Pop 1 £ Pop 2 Pop 1 < Pop 2 Pop 1 > Pop 2 H 0 Ha Note: di = x 1 i – x 2 i for ith observation © 2011 Pearson Education, Inc

Paired-Difference Experiment Small-Sample Test Example You work in Human Resources. You want to see if a training program is effective. You collect the following test score data: Name Before After Sam 85 94 Tamika 94 87 Brian 78 79 Mike 87 88 At the. 10 level of significance, was the training effective? © 2011 Pearson Education, Inc

Null Hypothesis Solution 1. Was the training effective? 2. Effective means ‘Before’ < ‘After’. 3. Statistically, this means B < A. 4. Rearranging terms gives B – A < 0. 5. Defining d = B – A and substituting into (4) gives d . 6. The alternative hypothesis is Ha: d 0. © 2011 Pearson Education, Inc

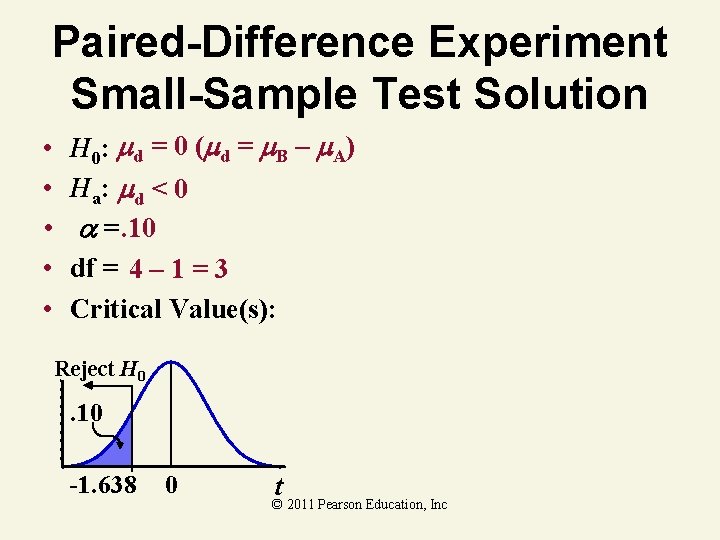
Paired-Difference Experiment Small-Sample Test Solution • • • H 0: d = 0 (

Paired-Difference Experiment Small-Sample Test Solution • • • H 0: d = 0 ( d = B – A) Test Statistic: Ha: d < 0 =. 10 df = 4 – 1 = 3 Critical Value(s): Decision: Reject H 0 Do not reject at =. 10 -1. 638 0 Conclusion: There is no evidence t© 2011 Pearson Education, training was effective Inc

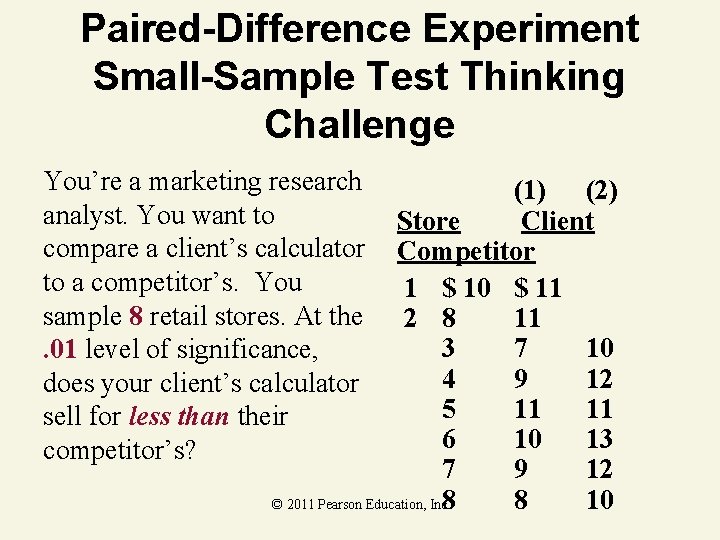
Paired-Difference Experiment Small-Sample Test Thinking Challenge You’re a marketing research analyst. You want to compare a client’s calculator to a competitor’s. You sample 8 retail stores. At the. 01 level of significance, does your client’s calculator sell for less than their competitor’s? (1) (2) Store Client Competitor 1 $ 10 $ 11 2 8 11 3 7 10 4 9 12 5 11 11 6 10 13 7 9 12 8 10 © 2011 Pearson Education, Inc 8

Paired-Difference Experiment Small-Sample Test Solution* • • • H 0: d = 0 ( d = 1 – 2) Ha: d < 0 =. 01 df = 8 – 1 = 7 Critical Value(s): Reject H 0 . 01 -2. 998 0 Test Statistic: Decision: Reject at =. 01 Conclusion: There is evidence client’s brand (1) sells for less t© 2011 Pearson Education, Inc

7. 4 Comparing Two Population Proportions: Independent Sampling © 2011 Pearson Education, Inc

Properties of the Sampling Distribution of (p 1 – p 2) 1. The mean of the sampling distribution of (p 1 – p 2); that is, is 2. The standard deviation of the sampling distribution of is 3. If the sample sizes n 1 and n 2 are large, the sampling distribution of is approximately normal. © 2011 Pearson Education, Inc

Large-Sample (1 – )% Confidence Interval for (p 1 – p 2) © 2011

Conditions Required for Valid Large-Sample Inferences about (p 1 – p 2) 1. The two samples are randomly selected in an independent manner from the two target populations. 2. The sample sizes, n 1 and n 2, are both large so that the sampling distribution of will be approximately normal. (This condition will be satisfied if both © 2011 Pearson Education, Inc

Large-Sample Test of Hypothesis about (p 1 – p 2) One-Tailed Test H 0: (p 1 – p 2) = 0 Ha: (p 1 – p 2) < 0 [or Ha: (p 1 – p 2) > 0 ] Test statistic: Rejection region: z < –z [or z > z when Ha: (p 1 – p 2) > 0 ] Note: © 2011 Pearson Education, Inc

Large-Sample Test of Hypothesis about (p 1 – p 2) Two-Tailed Test H 0:

Confidence Interval for p 1 – p 2 Example As personnel director, you want to test the perception of fairness of two methods of performance evaluation. 63 of 78 employees rated Method 1 as fair. 49 of 82 rated Method 2 as fair. Find a 99% confidence interval for the difference in perceptions. © 2011 Pearson Education, Inc

Confidence Interval for p 1 – p 2 Solution © 2011 Pearson Education, Inc

Hypotheses for Two Proportions Research Questions Hypothesis No Difference Any Difference Pop 1 ³

Test for Two Proportions Example As personnel director, you want to test the perception of fairness of two methods of performance evaluation. 63 of 78 employees rated Method 1 as fair. 49 of 82 rated Method 2 as fair. At the. 01 level of significance, is there a difference in perceptions? © 2011 Pearson Education, Inc

Test for Two Proportions Solution • • • H 0: p 1 – p

Test for Two Proportions Solution © 2011 Pearson Education, Inc

Test for Two Proportions Solution • • • H 0: p 1 – p 2 = 0 Ha: p 1 – p 2 0 =. 01 n 1 = 78 n 2 = 82 Critical Value(s): Reject H 0 . 005 – 2. 58 0 2. 58 . 005 Test Statistic: z = +2. 90 Decision: Reject at =. 01 Conclusion: There is evidence of a z difference in proportions © 2011 Pearson Education, Inc

Test for Two Proportions Thinking Challenge You’re an economist for the Department of Labor. You’re studying unemployment rates. In MA, 74 of 1500 people surveyed were unemployed. In CA, 129 of 1500 were unemployed. At the. 05 level of significance, does MA have a lower unemployment rate than CA? © 2011 Pearson Education, Inc MA CA

Test for Two Proportions Solution* • • • H 0: p. MA – p.

Test for Two Proportions Solution* • • • H 0: p. MA – p. CA = 0 Test Statistic: z = – 4. 00 Ha: p. MA – p. CA < 0 =. 05 n. MA = 1500 n. CA = 1500 Critical Value(s): Decision: Reject H 0 Reject at =. 05 Conclusion: -1. 645 0 z There is evidence MA is less than CA © 2011 Pearson Education, Inc

7. 5 Determining Sample Size © 2011 Pearson Education, Inc

Determination of Sample Size for Estimating µ 1 – µ 2 To estimate (μ 1 – μ 2) with a given margin of error ME and with confidence level (1 – ), use the following formula to solve for equal sample sizes that will achieve the desired reliability: You will need to substitute estimates for the values of and before solving for the sample size. These estimates might be sample variances and from prior sampling (e. g. , a pilot sample) or from an educated (and conservatively large) guess based on the range–that © 2011 Pearson Education, Inc is, s ≈ R/4.

Determination of Sample Size for Estimating p 1 – p 2 To estimate (p 1 – p 2) with a given margin of error ME and with confidence level (1 – ), use the following formula to solve for equal sample sizes that will achieve the desired reliability: You will need to substitute estimates for the values of p 1 and p 2 before solving for the sample size. These estimates might be based on prior samples, obtained from educated guesses, or, most conservatively, specified as p 1 = p 2 =© 2011. 5. Pearson Education, Inc

Sample Size Example What sample size is needed to estimate μ 1 – μ 2 with 95% confidence and a margin of error of 5. 8? Assume prior experience tells us σ1 =12 and σ2 =18. © 2011 Pearson Education, Inc

Sample Size Example What sample size is needed to estimate p 1 – p

7. 6 Comparing Two Population Variances: Independent Sampling © 2011 Pearson Education, Inc

F-Test for Equal Population Variances One-Tailed Test H 0: Ha : (or Ha: ) Test statistic: Rejection region: F > F where F is based on v 1 = numerator degrees of freedom and v 2 = denominator degrees of freedom; v 1 and v 2 are the degrees of freedom for the numerator and denominator sample ©variances, respectively. 2011 Pearson Education, Inc

F-Test for Equal Population Variances Two-Tailed Test H 0: Ha : Test statistic: Rejection region: F > F where F /2 is based on v 1 = numerator degrees of freedom and v 2 = denominator degrees of freedom; v 1 and v 2 are the degrees of freedom for the numerator and denominator sample ©variances, respectively. 2011 Pearson Education, Inc

Conditions Required for a Valid F -Test for Equal Variances 1. Both sampled populations

F-Test for Equal Variances Example You’re a financial analyst for Charles Schwab. You want to compare dividend yields between stocks listed on the NYSE & NASDAQ. You collect the following data: NYSE NASDAQ Number 21 25 Mean 3. 27 2. 53 Std Dev 1. 30 1. 16 Is there a difference in variances between the NYSE & NASDAQ at the. 05 level of significance? © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

F-Test for Equal Variances Solution • • H 0: 12 = 22 Ha: 12

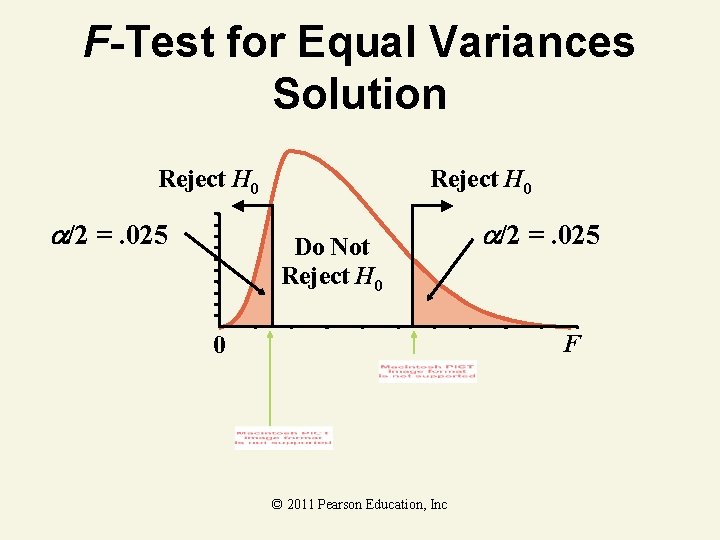
F-Test for Equal Variances Solution Reject H 0 /2 =. 025 Reject H 0

F-Test for Equal Variances Solution • • • H 0: 12 = 22 Ha: 12 22 . 05 1 20 2 24 Critical Value(s): Reject H 0 . 025 0. 415 . 025 2. 33 F Test Statistic: Decision: Do not reject at =. 05 Conclusion: There is no evidence of a difference in variances © 2011 Pearson Education, Inc

F-Test for Equal Variances Thinking Challenge You’re an analyst for the Light & Power Company. You want to compare the electricity consumption of single-family homes in two towns. You compute the following from a sample of homes: Town 1 Town 2 Number 25 21 Mean $ 85 $ 68 Std Dev $ 30 $ 18 At the. 05 level of significance, is there evidence of a difference in variances between the two towns? © 2011 Pearson Education, Inc

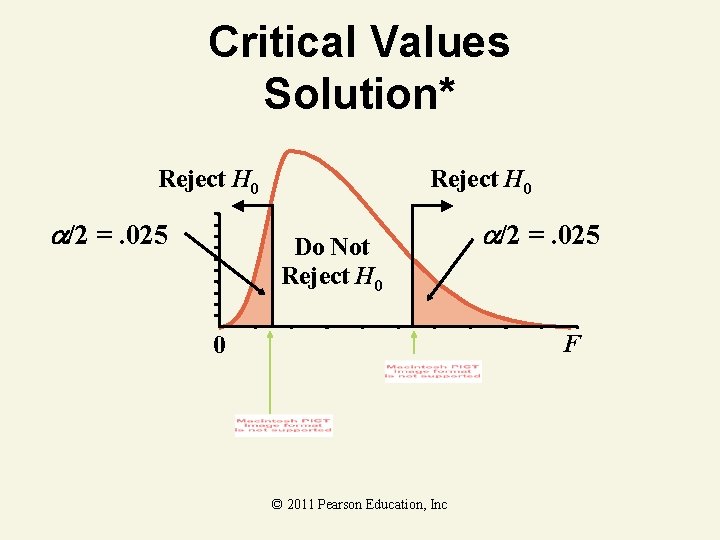
Critical Values Solution* Reject H 0 /2 =. 025 Reject H 0 Do Not

F-Test for Equal Variances Solution* • • • H 0: 12 = 22 Ha: 12 22 . 05 1 24 2 20 Critical Value(s): Reject H 0 . 025 0. 429 2. 41 Test Statistic: Decision: Reject at =. 05 F Conclusion: There is evidence of a difference in variances © 2011 Pearson Education, Inc

Key Ideas Key Words for Identifying the Target Parameter – Difference in means or averages d Paired difference in means or averages p 1 – p 2 Difference in proportions, fractions, percentages, rates Ratio (or difference) in variances, spreads © 2011 Pearson Education, Inc

Key Ideas Determining the Sample Size Estimating – : Estimating p – p :

Key Ideas Conditions Required for Inferences about µ 1 – µ 2 Large Samples: 1. Independent random samples 2. n 1 ≥ 30, n 2 ≥ 30 Small Samples: 1. Independent random samples 2. Both populations normal 3. © 2011 Pearson Education, Inc

Key Ideas Conditions Required for Inferences about Large or small Samples: 1. Independent random

Key Ideas Conditions Required for Inferences about µd Large Samples: 1. Random sample of paired differences 2. nd ≥ 30 Small Samples: 1. Random sample of paired differences 2. Population of differences is normal © 2011 Pearson Education, Inc

Key Ideas Conditions Required for Inferences about p 1 – p 2 Large Samples:

Key Ideas Using a Confidence Interval for (µ 1 – µ 2) or (p 1 – p 2) to Determine whether a Difference Exists 1. If the confidence interval includes all positive numbers (+, +): Infer µ 1> µ 2 or p 1 > p 2 2. If the confidence interval includes all negative numbers (–, –): Infer µ 1 < µ 2 or p 1 < p 2 3. If the confidence interval includes 0 (–, +): Infer no evidence or a difference © 2011 Pearson Education, Inc