2009 6 5 HoravaLifshitz Ref Chiral Primordial Gravitational

2009. 6. 5 大阪市立大学セミナー Horava-Lifshitz重力理論とはなにか？ 早田次郎 　京都大学理学研究科 Ref. Chiral Primordial Gravitational Waves from a Lifshitz Point T. Takahashi & J. Soda, ar. Xiv: 0904. 0554 [hep-th], to appear in Phys. Rev. Lett.

How to get to Planck scale? There are two well known the paths to reach the Planck scale. Hawking radiation GW Exponential red shift BH Quantum fluctuations inflation Exponential red shift Quantum fluctuations In reality, it would be difficult to observe Hawking radiation. However, we may be able to observe primordial gravitational waves! Hence, in this talk, I will mostly discuss an inflation.

The universe is so transparent for GW! The reaction rate is much smaller than the expansion rate in the cosmic history. reaction rate expansion rate Hence, PGW can carry the information of the Planck scale. Namely, one can see the very early universe! Indeed, we can indirectly observe PGW through CMB or directly observe PGW by LISA or DECIGO. What kind of smoking gun of the Planck scale can be expected?

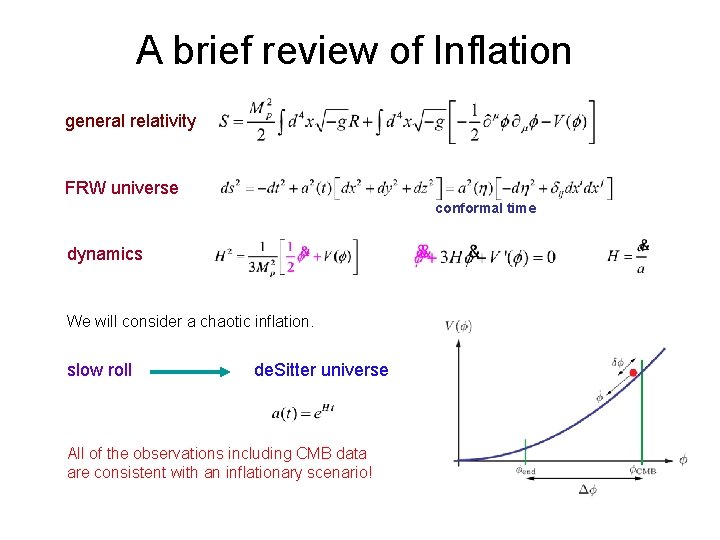
A brief review of Inflation general relativity FRW universe conformal time dynamics We will consider a chaotic inflation. slow roll de. Sitter universe All of the observations including CMB data are consistent with an inflationary scenario!

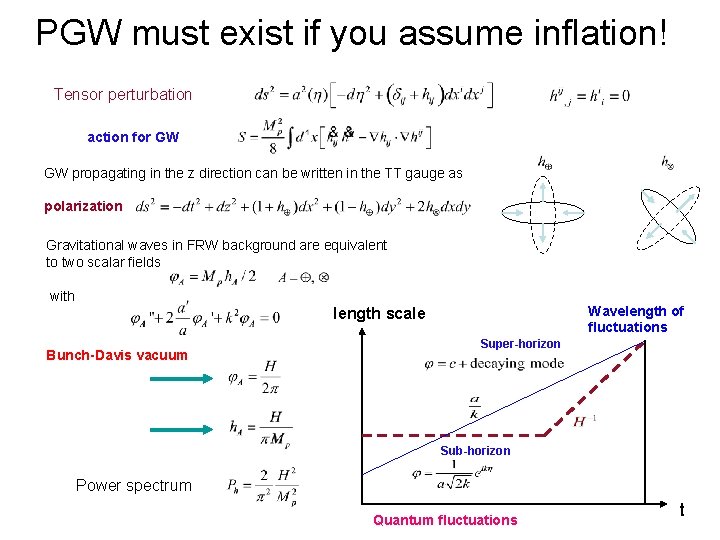
PGW must exist if you assume inflation! Tensor perturbation action for GW GW propagating in the z direction can be written in the TT gauge as polarization Gravitational waves in FRW background are equivalent to two scalar fields with Wavelength of fluctuations length scale Bunch-Davis vacuum Super-horizon Sub-horizon Power spectrum Quantum fluctuations t

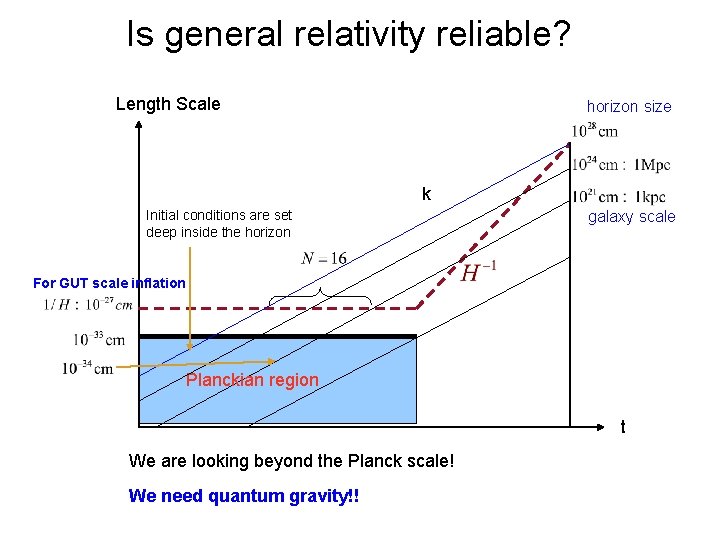
Is general relativity reliable? Length Scale horizon size k Initial conditions are set deep inside the horizon galaxy scale For GUT scale inflation Planckian region t We are looking beyond the Planck scale! We need quantum gravity!!

Quantum Gravity and Renormalizability A difficulty UV divergence in general relativity can not be renormalized Higher curvature improves the situation but suffers from ghosts That is why many people are studying string theory. However, string theory is rather large framework and not yet mature to discuss cosmology. Hence, it is worth seeking an alternative to string theory.

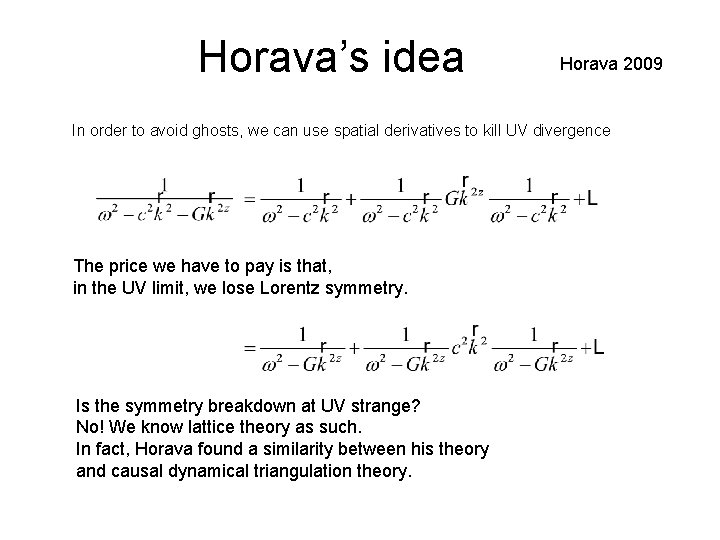
Horava’s idea Horava 2009 In order to avoid ghosts, we can use spatial derivatives to kill UV divergence The price we have to pay is that, in the UV limit, we lose Lorentz symmetry. Is the symmetry breakdown at UV strange? No! We know lattice theory as such. In fact, Horava found a similarity between his theory and causal dynamical triangulation theory.

Lifshitz-like anisotropic scaling In order to get a renormalizable theory, we need the anisotropic scaling Because of this, we do not have 4 -d diffeomorphism invariance. foliation preserving diffeomorphism ADM form lapse extrinsic curvature 3 d metric shift Horava 2009

Horava gravity – kinetic term The kinetic term should be Since the volume has dimension Coupling constants In the case and run under the renormalization. , we have an extra scalar degree of freedom. In the IR limit, we should have

Horava gravity – potential term detailed balance condition Horava 2009 Orlando & Reffert 2009 This guarantees the renormalizability of theory beyond power counting. The power counting renormalizable action with relevant deformation reads z = 3 UV gravity Cotton tensor relevant deformation

Horava gravity z=3 UV gravity z=1 IR gravity comments A parity violating term is required for theory to be renormalizable! We have a negative cosmological constant which must be compensated by the energy density of the matter. Cosmological constant problem! To recover the general relativity, we need rescale The speed of light and Newton constant are emergent quantities

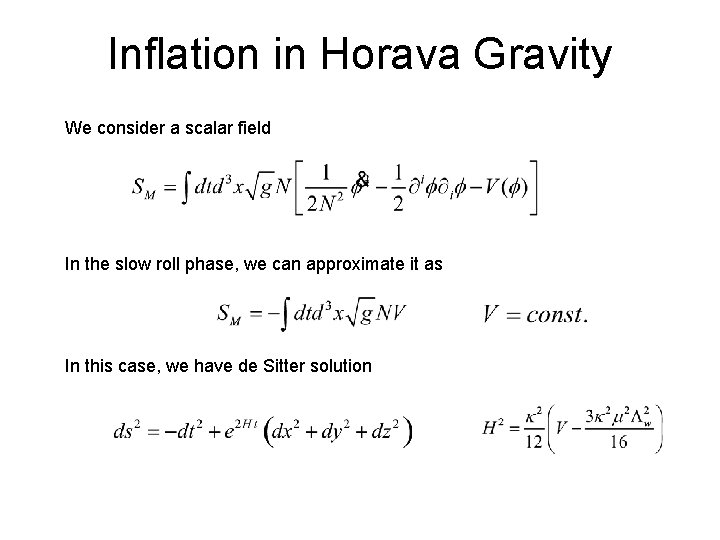
Inflation in Horava Gravity We consider a scalar field In the slow roll phase, we can approximate it as In this case, we have de Sitter solution

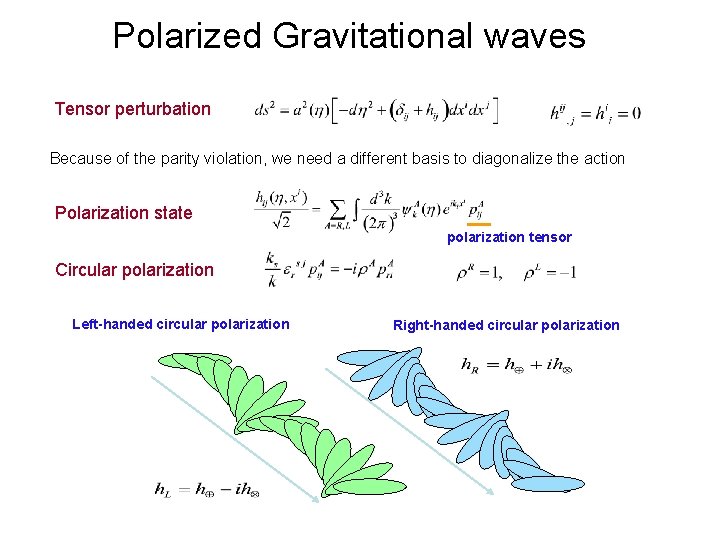
Polarized Gravitational waves Tensor perturbation Because of the parity violation, we need a different basis to diagonalize the action Polarization state polarization tensor Circular polarization Left-handed circular polarization Right-handed circular polarization

Action for gravitational waves

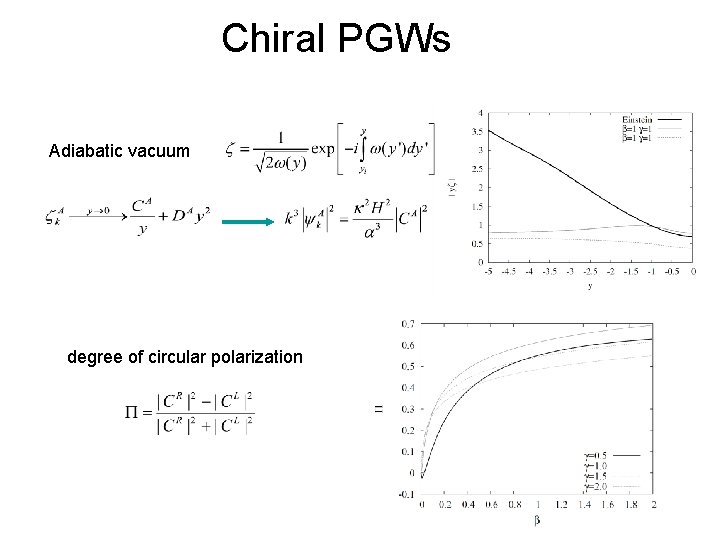
Chiral PGWs Adiabatic vacuum degree of circular polarization

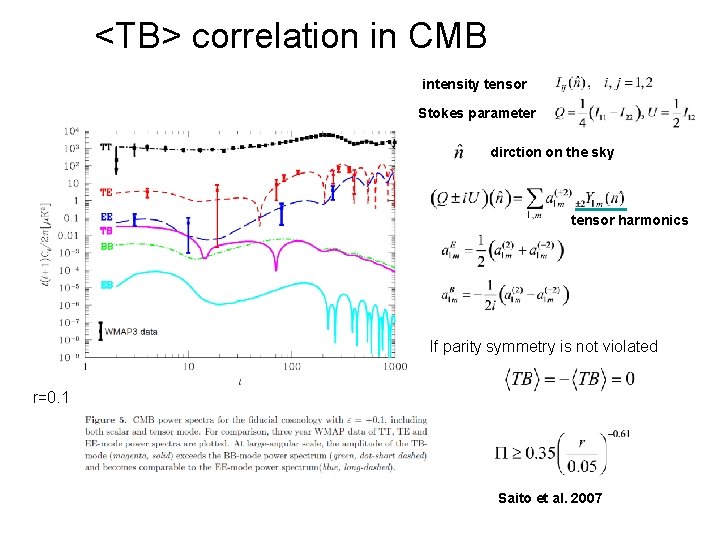
<TB> correlation in CMB intensity tensor Stokes parameter dirction on the sky tensor harmonics If parity symmetry is not violated r=0. 1 Saito et al. 2007

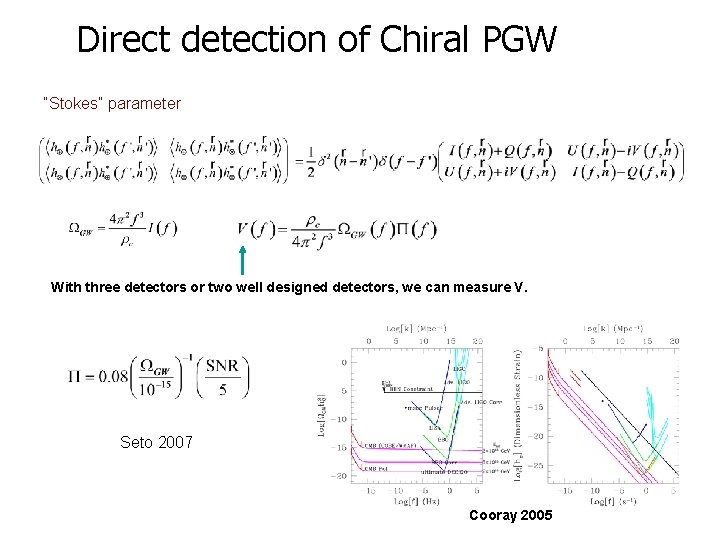
Direct detection of Chiral PGW “Stokes” parameter With three detectors or two well designed detectors, we can measure V. Seto 2007 Cooray 2005

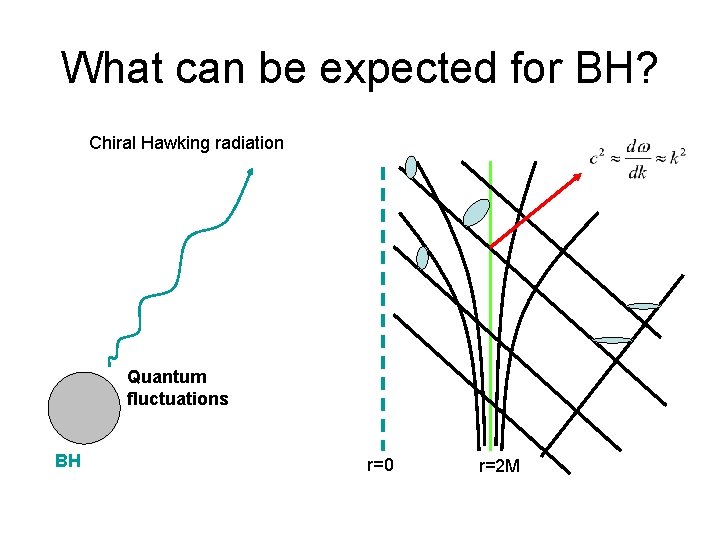
What can be expected for BH? Chiral Hawking radiation Quantum fluctuations BH r=0 r=2 M

Conclusion • We have looked beyond the Planck scale via Horava gravity and found that the spacetime is chiral, which can be tested by observing a circular polarization of primordial gravitational waves. This is a robust prediction of Horava gravity! The renormalizability yields parity violation, which is reminiscent of CKM parity violation.