20021111 Data base Label Setting Algorithm Label Correcting

運輸資訊 最短路徑演算法 卓訓榮 2002/11/11 Data base Label Setting Algorithm Label Correcting Algorithm

Data Base
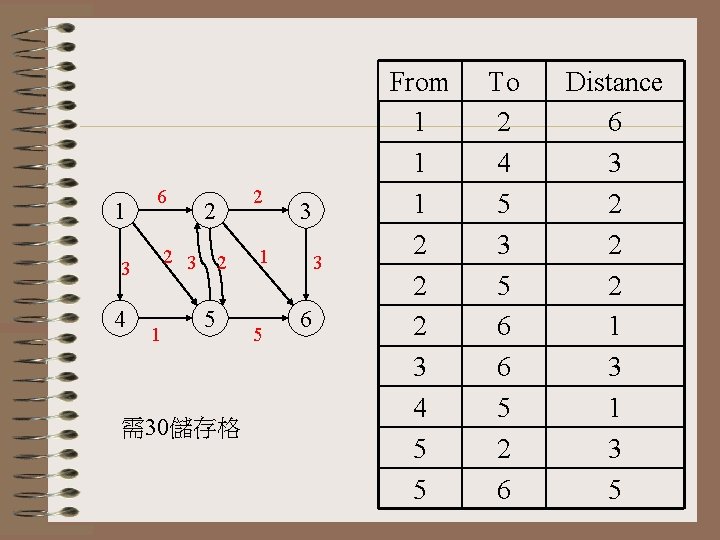
1 6 4 2 2 3 3 1 2 2 5 需30儲存格 3 1 5 3 6 From 1 1 1 2 2 2 3 4 5 5 To 2 4 5 3 5 6 6 5 2 6 Distance 6 3 2 2 2 1 3 5
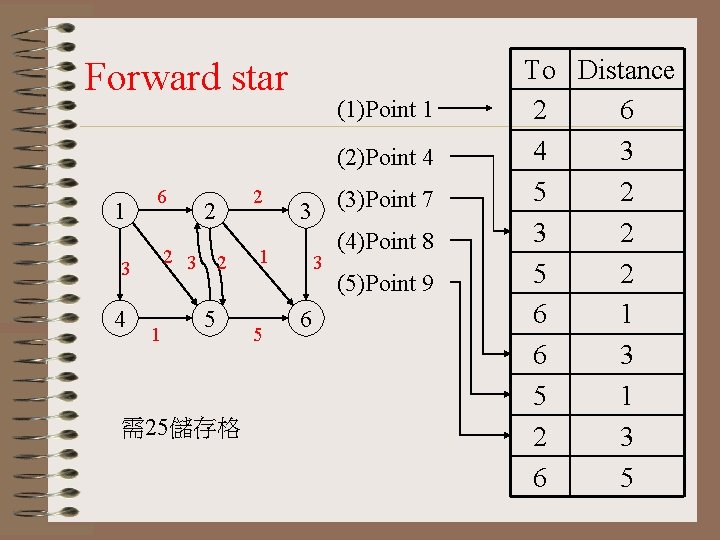
Forward star (1)Point 1 (2)Point 4 1 6 4 2 2 3 3 1 2 2 5 需25儲存格 1 5 (3)Point 7 3 3 6 (4)Point 8 (5)Point 9 To Distance 2 6 4 3 5 2 3 2 5 2 6 1 6 3 5 1 2 3 6 5

Label Setting Algorithm



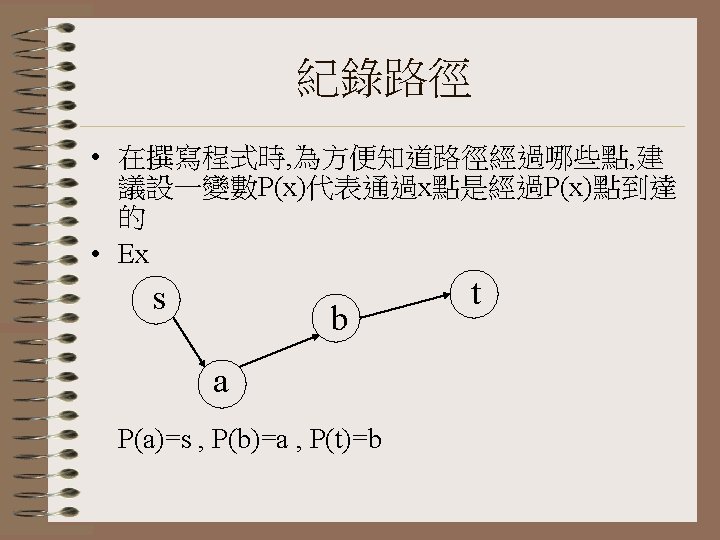
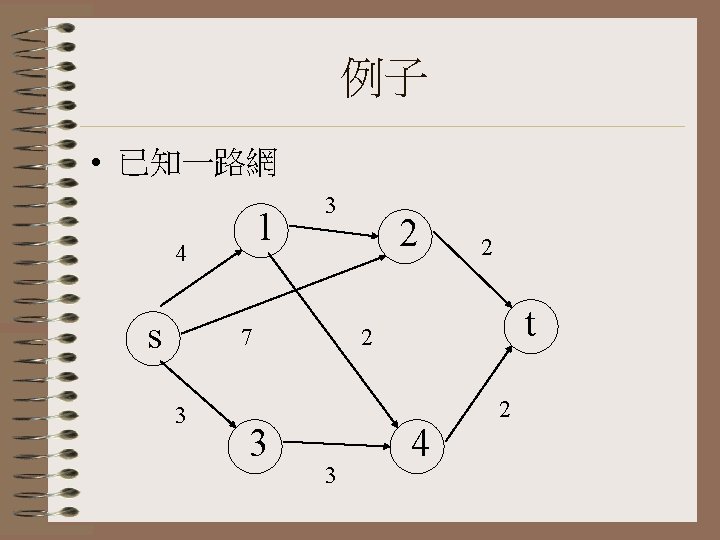
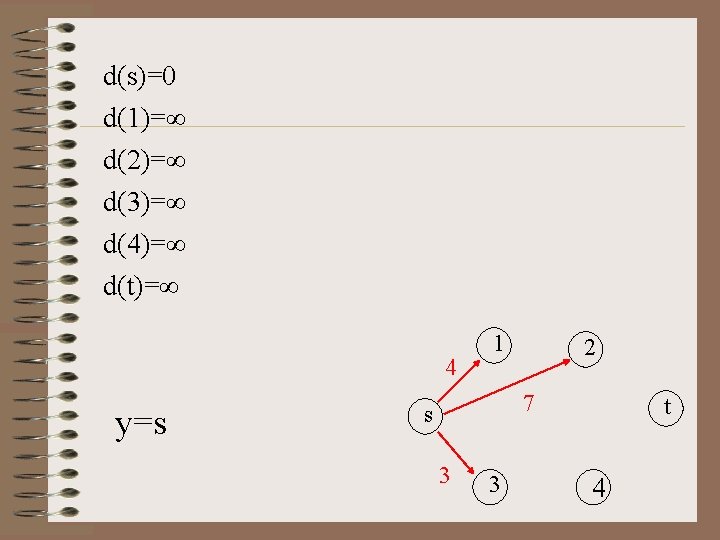
d(s)=0 d(1)=∞ d(2)=∞ d(3)=∞ d(4)=∞ d(t)=∞ 4 y=s 1 2 7 s 3 3 t 4
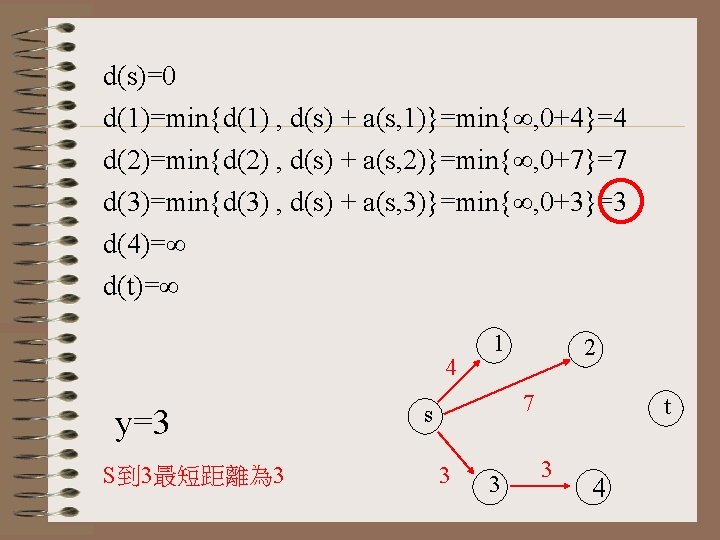
d(s)=0 d(1)=min{d(1) , d(s) + a(s, 1)}=min{∞, 0+4}=4 d(2)=min{d(2) , d(s) + a(s, 2)}=min{∞, 0+7}=7 d(3)=min{d(3) , d(s) + a(s, 3)}=min{∞, 0+3}=3 d(4)=∞ d(t)=∞ 4 y=3 S到 3最短距離為 3 1 2 7 s 3 3 t 3 4
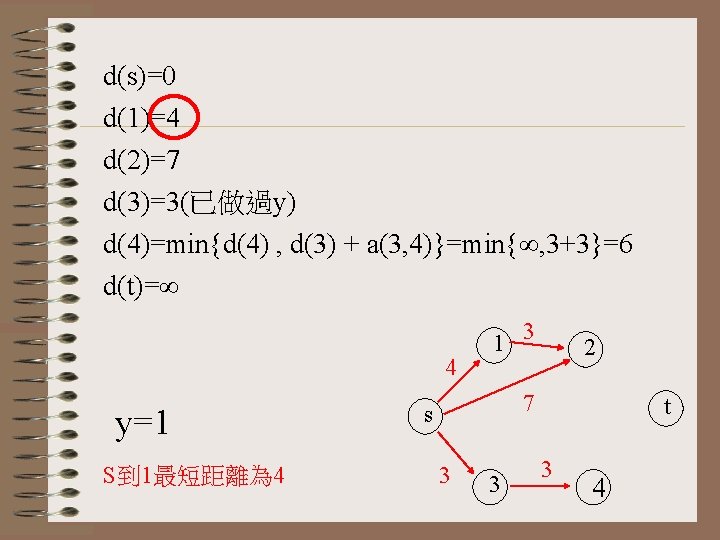
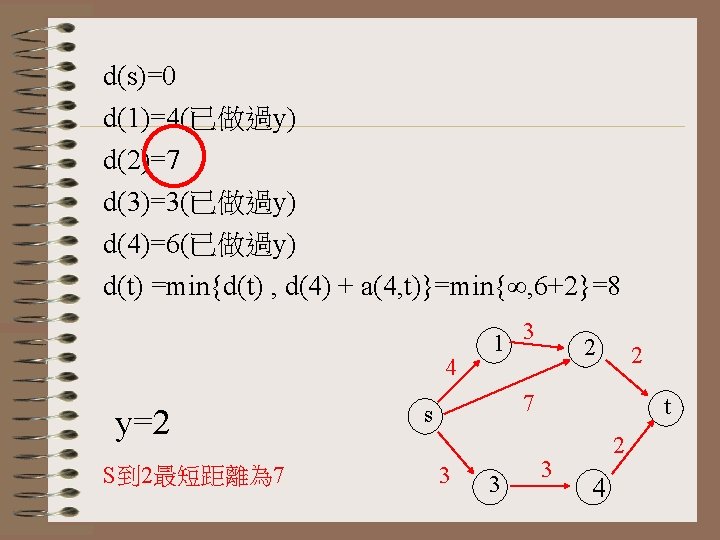
d(s)=0 d(1)=4 d(2)=7 d(3)=3(已做過y) d(4)=min{d(4) , d(3) + a(3, 4)}=min{∞, 3+3}=6 d(t)=∞ 4 y=1 S到 1最短距離為 4 1 3 2 7 s 3 3 t 3 4
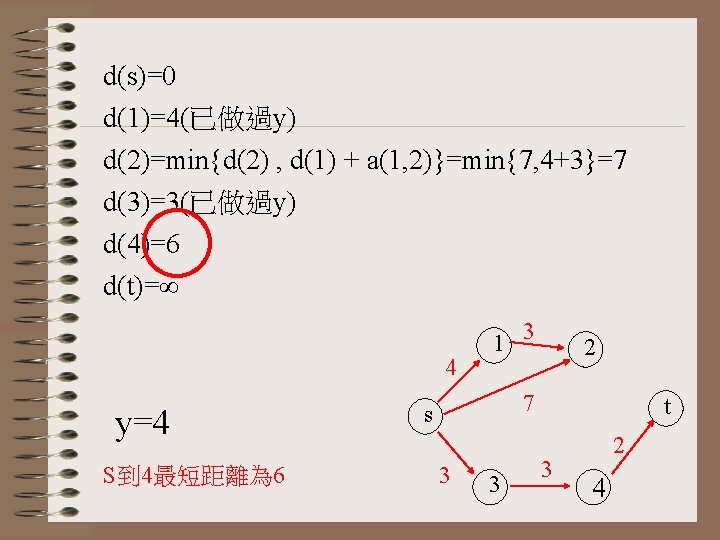
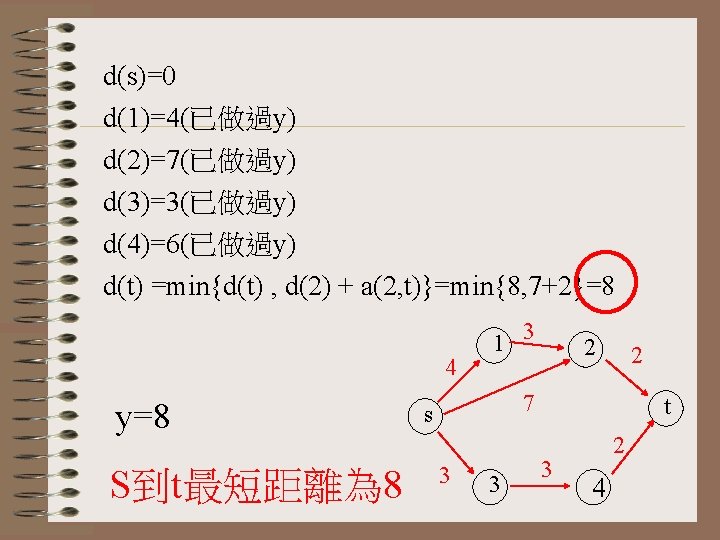
d(s)=0 d(1)=4(已做過y) d(2)=min{d(2) , d(1) + a(1, 2)}=min{7, 4+3}=7 d(3)=3(已做過y) d(4)=6 d(t)=∞ 4 y=4 S到 4最短距離為 6 1 3 2 7 s 3 3 t 3 2 4

Label Correcting Algorithm



Algorithm • 起始條件 k=0 , d(s)=0 , when S={s} , k=k+1 , go to Step 1

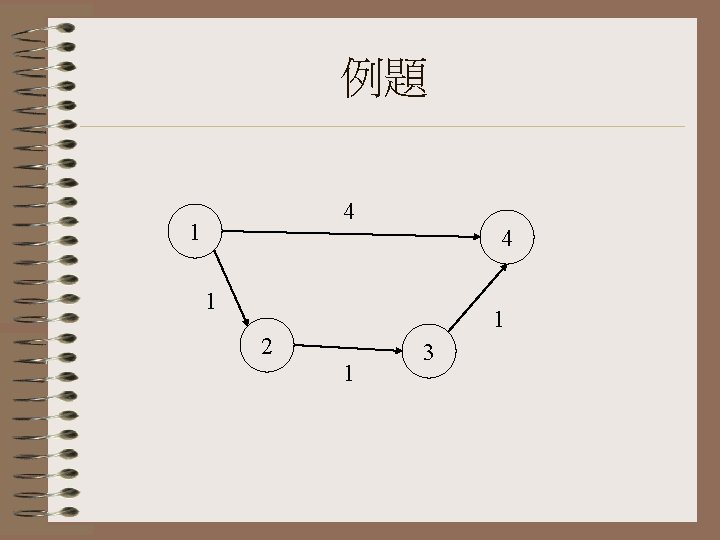
例題 4 1 1 2 1 3
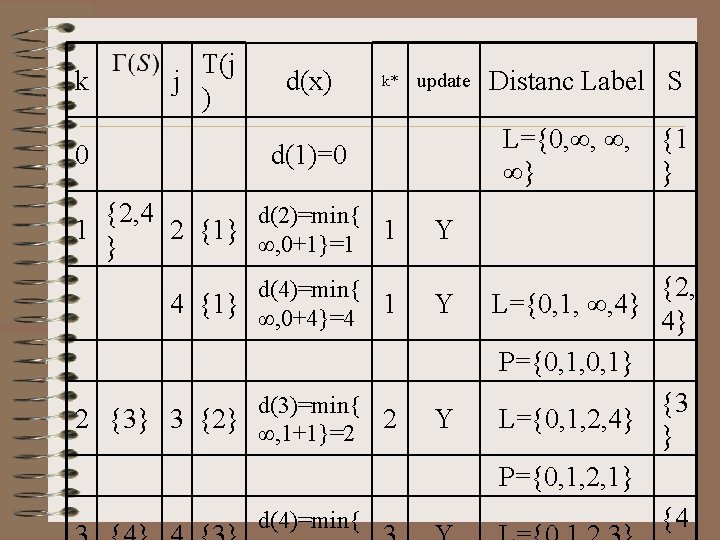
k 0 T(j j ) d(x) k* update L={0, ∞, ∞, ∞} d(1)=0 {2, 4 d(2)=min{ 1 2 {1} ∞, 0+1}=1 1 } {1 } Y d(4)=min{ 4 {1} ∞, 0+4}=4 1 Y d(3)=min{ 2 {3} 3 {2} ∞, 1+1}=2 2 Y d(4)=min{ Distanc Label S {2, L={0, 1, ∞, 4} 4} P={0, 1, 0, 1} {3 L={0, 1, 2, 4} } P={0, 1, 2, 1} {4
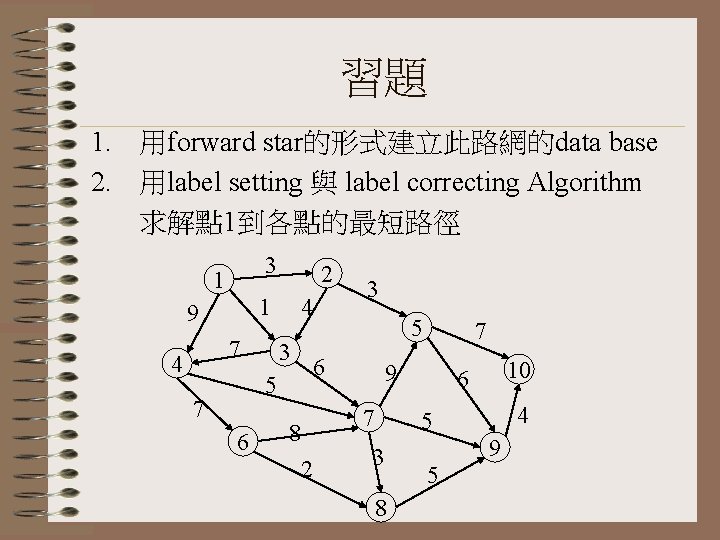
習題 1. 用forward star的形式建立此路網的data base 2. 用label setting 與 label correcting Algorithm 求解點 1到各點的最短路徑 3 1 1 9 7 4 2 4 3 5 6 5 7 6 3 9 7 8 2 7 10 6 4 5 3 8 9 5
- Slides: 24