20012022 FACTORISING QUADRATICS Learning Objectives By the end

20/01/2022 FACTORISING QUADRATICS Learning Objectives By the end of the lesson you should : 1. Be able to factorise a quadratic where the co-efficient of x 2 is 1.

Factorising a Quadratic • + Tells us that the signs must be the same Tells us that the numbers are the products of 6. Either 1 and 6 or 2 and 3 Tells us that the sum or difference between the numbers must be 7. + tells us that because we already know both signs are the same they are both +

Factorising a Quadratic • + Tells us that the signs must be the same Tells us that the numbers are the products of 6. Either 1 and 6 or 2 and 3 Tells us that the sum or difference between the numbers must be 7. + tells us that because we already know both signs are the same they are both -

Factorising a Quadratic • - Tells us that the signs must be different Tells us that the numbers are the products of 4. Either 1 and 4 or 2 and 2 Tells us that the sum or difference between the numbers must be 3. + Tells us that the bigger number goes with the minus.

Factorising a Quadratic • - Tells us that the signs must be different Tells us that the numbers are the products of 4. Either 1 and 4 or 2 and 2 Tells us that the sum or difference between the numbers must be 3. - Tells us that the bigger number goes with the minus.

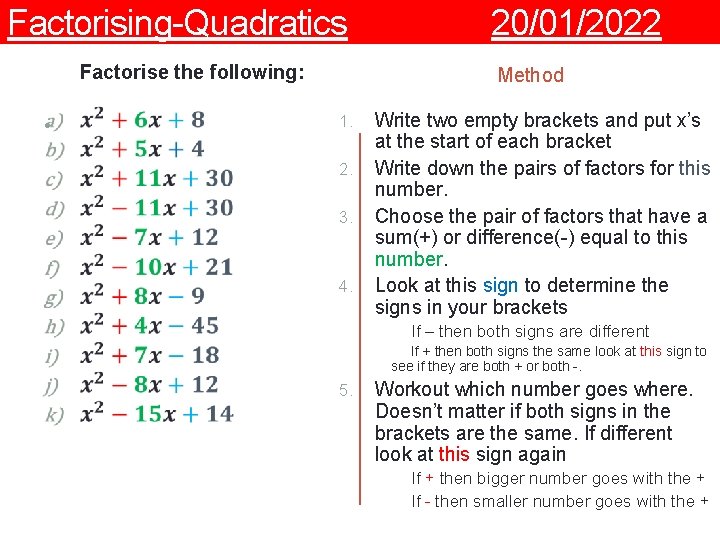
Factorising-Quadratics Factorise the following: • 20/01/2022 Method 1. 2. 3. 4. Write two empty brackets and put x’s at the start of each bracket Write down the pairs of factors for this number. Choose the pair of factors that have a sum(+) or difference(-) equal to this number. Look at this sign to determine the signs in your brackets If – then both signs are different If + then both signs the same look at this sign to see if they are both + or both -. 5. Workout which number goes where. Doesn’t matter if both signs in the brackets are the same. If different look at this sign again If + then bigger number goes with the + If - then smaller number goes with the +

Factorisng Quadratic Trinomials with Leading Coefficient Other Than One 1. Multiply the leading coefficient and the constant together. 2. List all possible factors of the result from step one. 3. Determine which factors will add together to give the middle coefficient. 4. Write the middle coefficient as the sum of the factors using the results from step three and rewrite the polynomial. 5. Group the first two terms and the last two terms together. 6. Take the Highest Common Factor (HCF) from each group. 7. Factor the HCF again.

Factorise and solve the following: •