2 Probability Distribution Binomial Distribution Poisson Distribution 20201124


2 Ø 機率分布(Probability Distribution) Ø 二項分布(Binomial Distribution) Ø 卜瓦松分布(Poisson Distribution) 2020/11/24 Jen-pei Liu, Ph. D

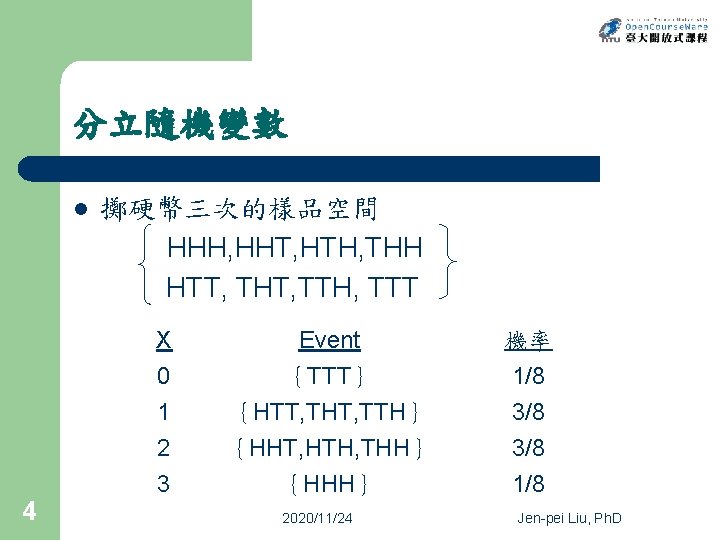
分立隨機變數 l 4 擲硬幣三次的樣品空間 HHH, HHT, HTH, THH HTT, THT, TTH, TTT X 0 1 2 Event {TTT} {HTT, THT, TTH} {HHT, HTH, THH} 機率 3 {HHH} 1/8 2020/11/24 1/8 3/8 Jen-pei Liu, Ph. D


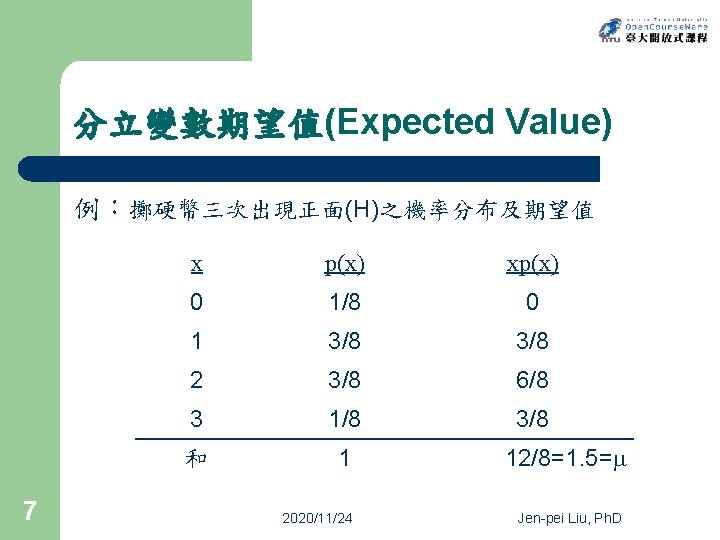
分立變數期望值(Expected Value) 例:擲硬幣三次出現正面(H)之機率分布及期望值 7 x p(x) xp(x) 0 1/8 0 1 3/8 2 3/8 6/8 3 1/8 3/8 和 1 2020/11/24 12/8=1. 5= Jen-pei Liu, Ph. D
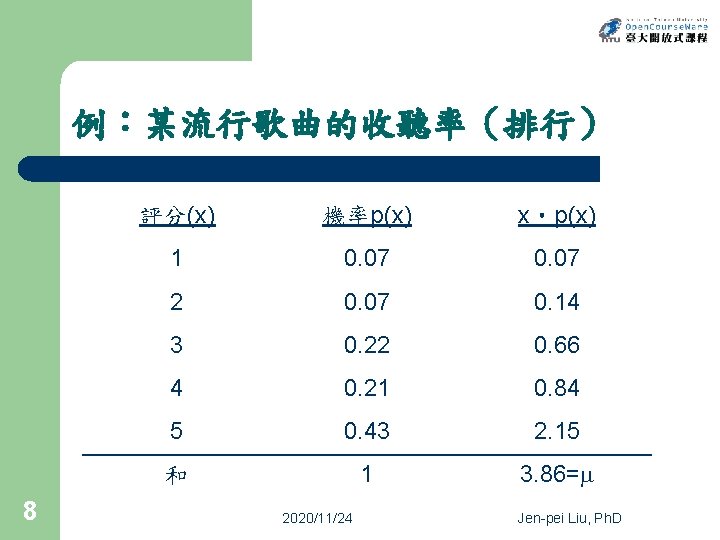
例:某流行歌曲的收聽率(排行) 8 評分(x) 機率p(x) x‧p(x) 1 0. 07 2 0. 07 0. 14 3 0. 22 0. 66 4 0. 21 0. 84 5 0. 43 2. 15 和 1 3. 86= 2020/11/24 Jen-pei Liu, Ph. D
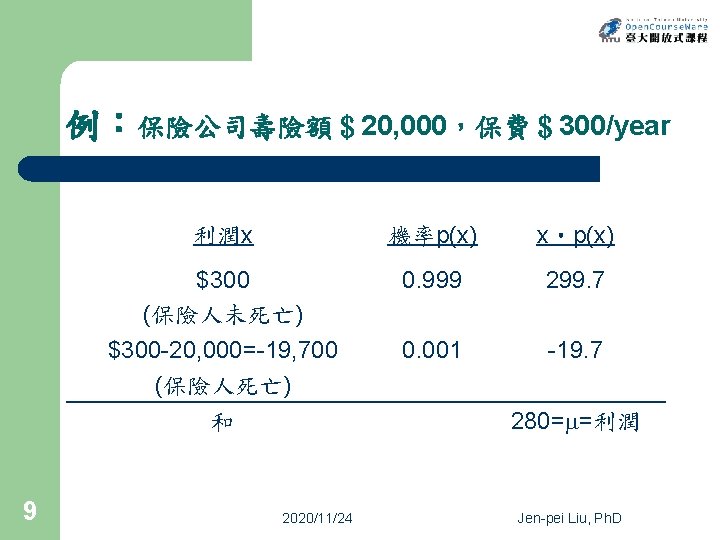
例:保險公司壽險額$20, 000,保費$300/year 利潤x 機率p(x) x‧p(x) $300 (保險人未死亡) 0. 999 299. 7 $300 -20, 000=-19, 700 (保險人死亡) 0. 001 -19. 7 280= =利潤 和 9 2020/11/24 Jen-pei Liu, Ph. D


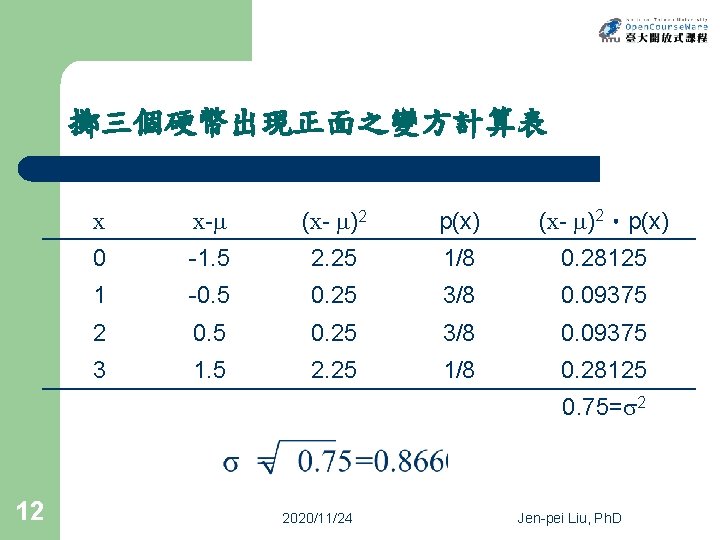
擲三個硬幣出現正面之變方計算表 x x- (x- )2 p(x) (x- )2‧p(x) 0 -1. 5 2. 25 1/8 0. 28125 1 -0. 5 0. 25 3/8 0. 09375 2 0. 5 0. 25 3/8 0. 09375 3 1. 5 2. 25 1/8 0. 28125 0. 75= 2 12 2020/11/24 Jen-pei Liu, Ph. D




二項分佈(Binomial distribution) l 樣品空間 SSS SSF SFS FSS FFS FSF SFF FFF X=2之事件包含的結果為 {SSF, SFS, FSS} 16 2020/11/24 Jen-pei Liu, Ph. D

二項分佈(Binomial distribution) P(SSF)=P(S)P(F)=(0. 4)(0. 6)=(0. 4)20. 6 P(SFS)=P(S)P(F)P(S)=(0. 4)(0. 6)(0. 4)=(0. 4)20. 6 P(FSS)=P(F)P(S)=(0. 6)(0. 4)=(0. 4)20. 6 P(X=2)=P(SSF)+P(SFS)+P(FSS) =(0. 4)20. 6+(0. 4)20. 6 =3(0. 4)20. 6 17 2020/11/24 Jen-pei Liu, Ph. D



二項分佈(Binomial Distribution) 20 2020/11/24 Jen-pei Liu, Ph. D

二項分佈(Binomial Distribution) 21 2020/11/24 Jen-pei Liu, Ph. D

二項分佈(Binomial Distribution) 22 2020/11/24 Jen-pei Liu, Ph. D





二項分佈(Binomial Distribution) 故至少有8位居民贊成之機率為 1 -0. 0042=0. 9958 (2)有10至 14位居民贊成之機率為 Pr(10≦X≦ 14) =P(X≦ 14)-P(X≦ 9) =0. 9648 -0. 0611=0. 9037 27 2020/11/24 Jen-pei Liu, Ph. D



卜瓦松分布(Poisson Distribution) 30 2020/11/24 Jen-pei Liu, Ph. D
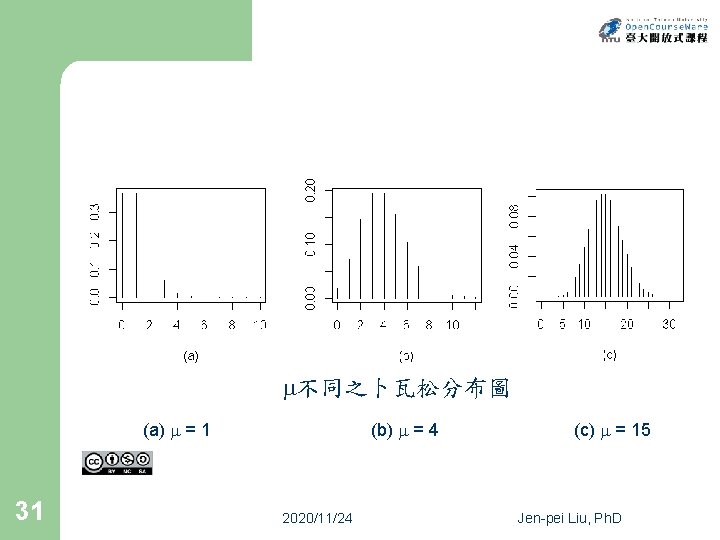
不同之卜瓦松分布圖 (a) = 1 31 (b) = 4 2020/11/24 (c) = 15 Jen-pei Liu, Ph. D


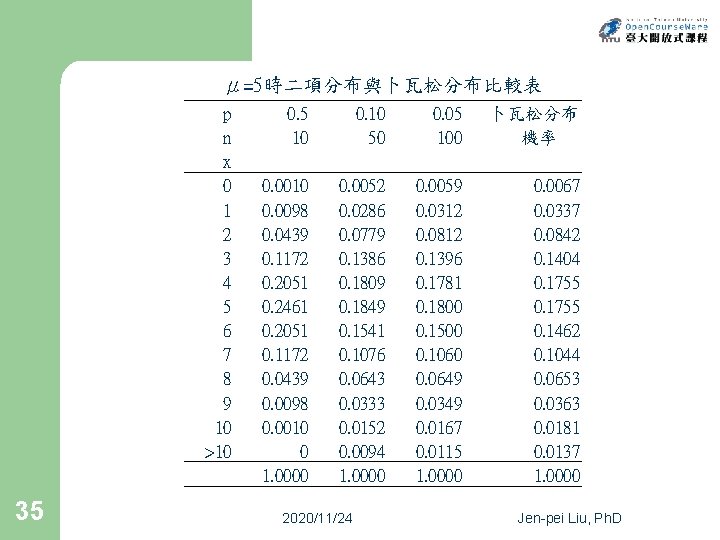
μ=5時二項分布與卜瓦松分布比較表 p n x 0 1 2 3 4 5 6 7 8 9 10 >10 35 0. 5 10 0. 10 50 0. 0010 0. 0098 0. 0439 0. 1172 0. 2051 0. 2461 0. 2051 0. 1172 0. 0439 0. 0098 0. 0010 0 1. 0000 0. 05 100 0. 0052 0. 0286 0. 0779 0. 1386 0. 1809 0. 1849 0. 1541 0. 1076 0. 0643 0. 0333 0. 0152 0. 0094 1. 0000 2020/11/24 卜瓦松分布 機率 0. 0059 0. 0312 0. 0812 0. 1396 0. 1781 0. 1800 0. 1500 0. 1060 0. 0649 0. 0349 0. 0167 0. 0115 1. 0000 0. 0067 0. 0337 0. 0842 0. 1404 0. 1755 0. 1462 0. 1044 0. 0653 0. 0363 0. 0181 0. 0137 1. 0000 Jen-pei Liu, Ph. D

習題: 37 l P. 105: 2, 3 l P. 106: 5 2020/11/24 Jen-pei Liu, Ph. D

- Slides: 38