2 nd lecture Basic Thermodynamics Fluid Mechanics Definitions

2 nd lecture Basic Thermodynamics, Fluid Mechanics: Definitions of Efficiency

The equation of continuity (cn is the normal velocity component to the flow surface) If A 1 and A 2 are the flow areas at stations 1 and 2 along a passage respectively, then The first law of thermodynamics - internal energy During a change of state from 1 to 2, there is a change in the property internal energy, For an infinitesimal change of state

The steady flow energy equation

The momentum equation- Newton’s second law of motion This equation is the one-dimensional form of the steady flow momentum equation. Euler’s equation of motion Bernoulli’s equation

Moment of momentum For a system of mass m, the vector sum of the moments of all external forces acting on the system about some arbitrary axis A A fixed in space is equal to the time rate of change of angular momentum of the system about that axis, i. e. where r is distance of the mass centre from the axis of rotation measured along the normal to the axis and c the velocity component mutually perpendicular to both the axis and radius vector r. For a control volume the law of momentum can be obtained. The figure shows the control volume enclosing the rotor of a generalized turbomachine. Swirling fluid enters the control volume at radius r 1 with tangential velocity c 1 and leaves at radius r 2 with tangential velocity c 2. For one-dimensional steady flow

Euler’s pump and turbine equations For a pump or compressor rotor running at angular velocity , the rate at which the rotor does work on the fluid is The work done on the fluid per unit mass or specific work, is This equation is referred to as Euler’s pump equation. For a turbine the fluid does work on the rotor and the sign for work is then reversed. Thus, the specific work is This equation is the Euler’s turbine equation.

Defining rothalpy In a compressor or pump the specific work done on the fluid equals the rise in stagnation enthalpy. Thus, combining the angular momentum equation with the energy equation we get After some rearranging of this equation and rewriting , we get The function I has the name rothalpy, rotational stagnation enthalpy. As the value of rothalpy is apparently unchanged between entry and exit of the impeller it is deduced that it must be constant along the flow lines between these two stations. Thus, the rothalpy can be written generally as The second law of thermodynamics- entropy The property called entropy, for a finite change of state, is then defined as

Gibbs equation For a system of mass m undergoing a reversible process d. Q = d. QR = m. Tds and d. W =d. WR = mpdv. In the absence of motion, gravity and other effects the first law of thermodynamics becomes With h = u+ pv then dh = du + pdv + vdp and then

Definitions of efficiency Efficiency of turbines the overall efficiency 0 The isentropic efficiency t or hydraulic efficiency h for a turbine is, the mechanical efficiency m, which is simply the ratio of shaft power to rotor power, is

For an incremental change of state through a turbomachine the steady flow energy equation can be written as From the second law of thermodynamics rearranging For a reversible adiabatic process

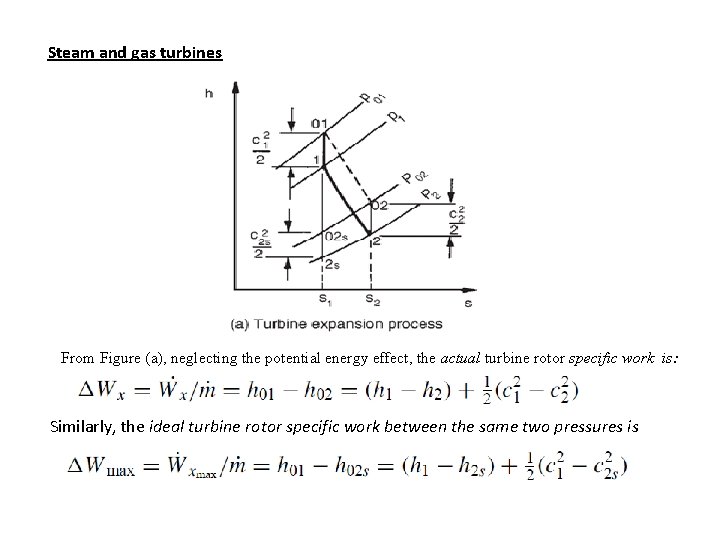
Steam and gas turbines From Figure (a), neglecting the potential energy effect, the actual turbine rotor specific work is: Similarly, the ideal turbine rotor specific work between the same two pressures is

Total-to-total efficiency The turbine and stage adiabatic efficiency , is the total-to-total efficiency and is defined as Total-to-static efficiency ts. When the exhaust kinetic energy is not usefully employed and entirely wasted, the relevant adiabatic efficiency is the total-to-static efficiency ts. If the difference between inlet and outlet kinetic energies is small Hydraulic turbines The turbine hydraulic efficiency h, is defined as the work supplied by the rotor in unit time divided by the hydrodynamic energy difference of the fluid per unit time,