2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES In






















































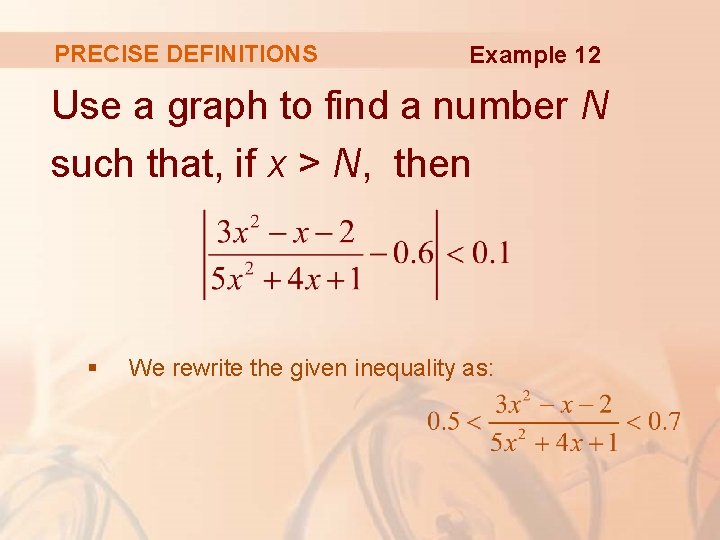






- Slides: 75

2 LIMITS AND DERIVATIVES

LIMITS AND DERIVATIVES In Sections 2. 2 and 2. 4, we investigated infinite limits and vertical asymptotes. § There, we let x approach a number. § The result was that the values of y became arbitrarily large (positive or negative).

LIMITS AND DERIVATIVES 2. 6 Limits at Infinity: Horizontal Asymptotes In this section, we: Let x become arbitrarily large (positive or negative) and see what happens to y.

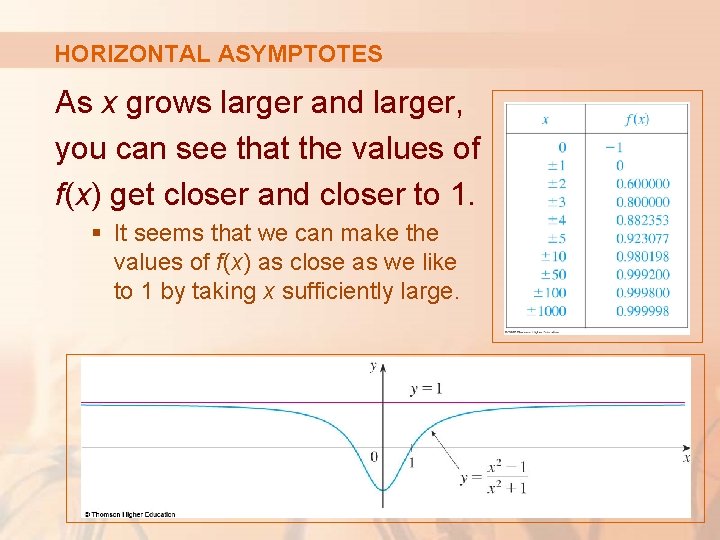
HORIZONTAL ASYMPTOTES Let’s begin by investigating the behavior of the function f defined by as x becomes large.

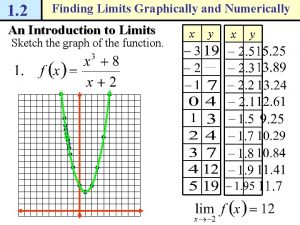
HORIZONTAL ASYMPTOTES The table gives values of this function correct to six decimal places. The graph of f has been drawn by a computer in the figure.

HORIZONTAL ASYMPTOTES As x grows larger and larger, you can see that the values of f(x) get closer and closer to 1. § It seems that we can make the values of f(x) as close as we like to 1 by taking x sufficiently large.

HORIZONTAL ASYMPTOTES This situation is expressed symbolically by writing In general, we use the notation to indicate that the values of f(x) become closer and closer to L as x becomes larger and larger.

HORIZONTAL ASYMPTOTES 1. Definition Let f be a function defined on some interval. Then, means that the values of f(x) can be made arbitrarily close to L by taking x sufficiently large.

HORIZONTAL ASYMPTOTES Another notation for as is § The symbol does not represent a number. § Nonetheless, the expression is often read as: “the limit of f(x), as x approaches infinity, is L” or “the limit of f(x), as x becomes infinite, is L” or “the limit of f(x), as x increases without bound, is L”

HORIZONTAL ASYMPTOTES The meaning of such phrases is given by Definition 1. A more precise definition—similar to the definition of Section 2. 4—is given at the end of this section.

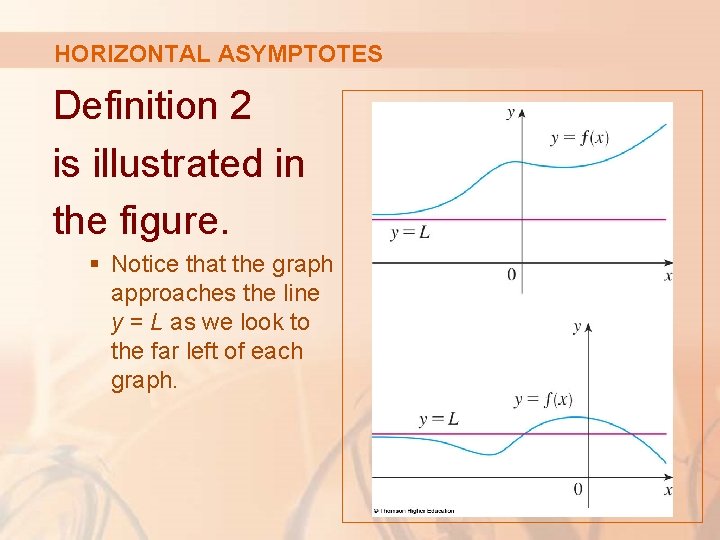
HORIZONTAL ASYMPTOTES Geometric illustrations of Definition 1 are shown in the figures. § Notice that there are many ways for the graph of f to approach the line y = L (which is called a horizontal asymptote) as we look to the far right of each graph.

HORIZONTAL ASYMPTOTES Referring to the earlier figure, we see that, for numerically large negative values of x, the values of f(x) are close to 1. § By letting x decrease through negative values without bound, we can make f(x) as close as we like to 1.

HORIZONTAL ASYMPTOTES This is expressed by writing The general definition is as follows.

HORIZONTAL ASYMPTOTES 2. Definition Let f be a function defined on some interval. Then, means that the values of f(x) can be made arbitrarily close to L by taking x sufficiently large negative.

HORIZONTAL ASYMPTOTES Again, the symbol does not represent a number. However, the expression is often read as: “the limit of f(x), as x approaches negative infinity, is L”

HORIZONTAL ASYMPTOTES Definition 2 is illustrated in the figure. § Notice that the graph approaches the line y = L as we look to the far left of each graph.

HORIZONTAL ASYMPTOTES 3. Definition The line y = L is called a horizontal asymptote of the curve y = f(x) if either

HORIZONTAL ASYMPTOTES 3. Definition For instance, the curve illustrated in the earlier figure has the line y = 1 as a horizontal asymptote because

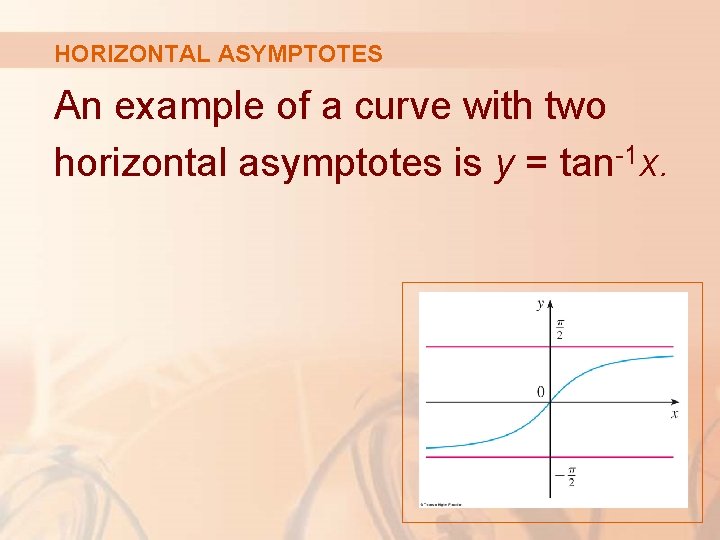
HORIZONTAL ASYMPTOTES An example of a curve with two horizontal asymptotes is y = tan-1 x.

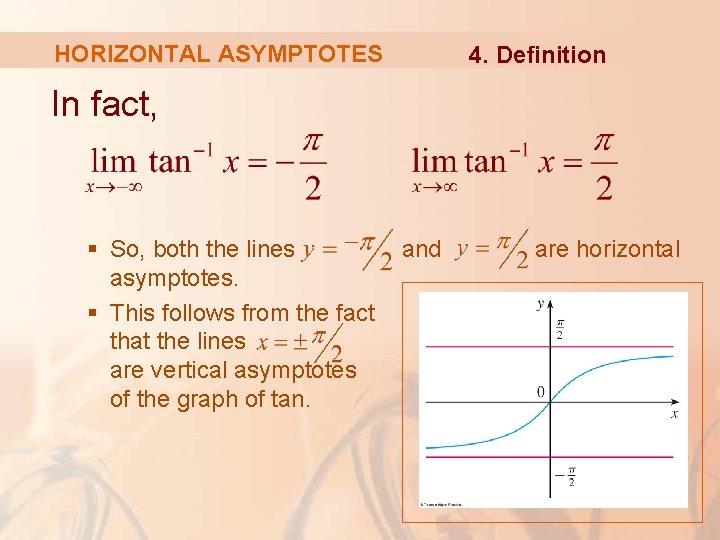
HORIZONTAL ASYMPTOTES 4. Definition In fact, § So, both the lines asymptotes. § This follows from the fact that the lines are vertical asymptotes of the graph of tan. and are horizontal

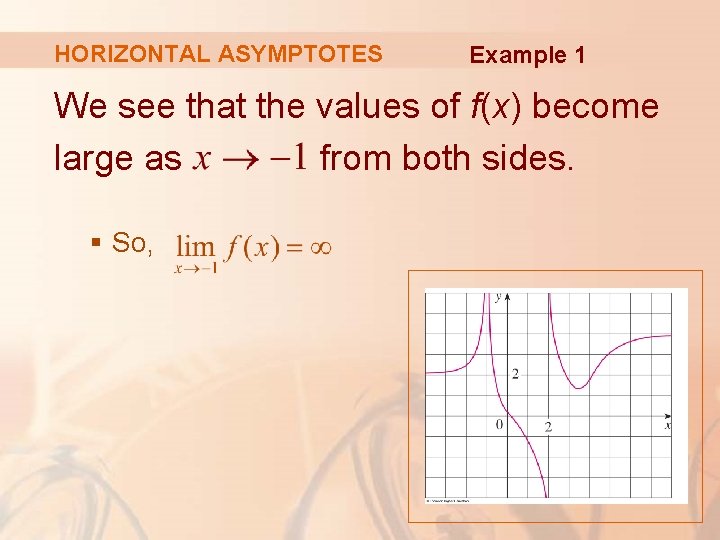
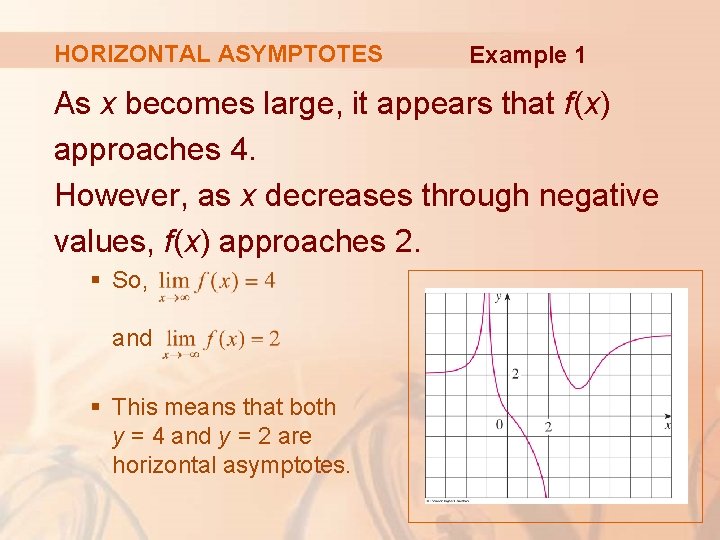
HORIZONTAL ASYMPTOTES Example 1 Find the infinite limits, limits at infinity, and asymptotes for the function f whose graph is shown in the figure.

HORIZONTAL ASYMPTOTES Example 1 We see that the values of f(x) become large as from both sides. § So,

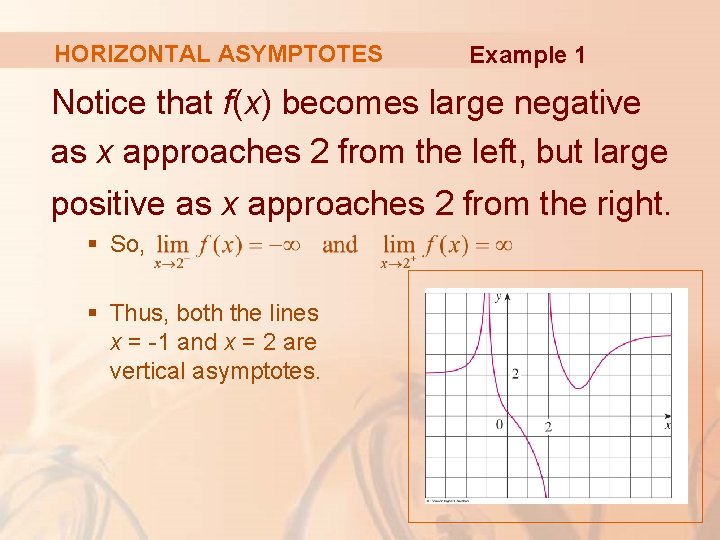
HORIZONTAL ASYMPTOTES Example 1 Notice that f(x) becomes large negative as x approaches 2 from the left, but large positive as x approaches 2 from the right. § So, § Thus, both the lines x = -1 and x = 2 are vertical asymptotes.

HORIZONTAL ASYMPTOTES Example 1 As x becomes large, it appears that f(x) approaches 4. However, as x decreases through negative values, f(x) approaches 2. § So, and § This means that both y = 4 and y = 2 are horizontal asymptotes.

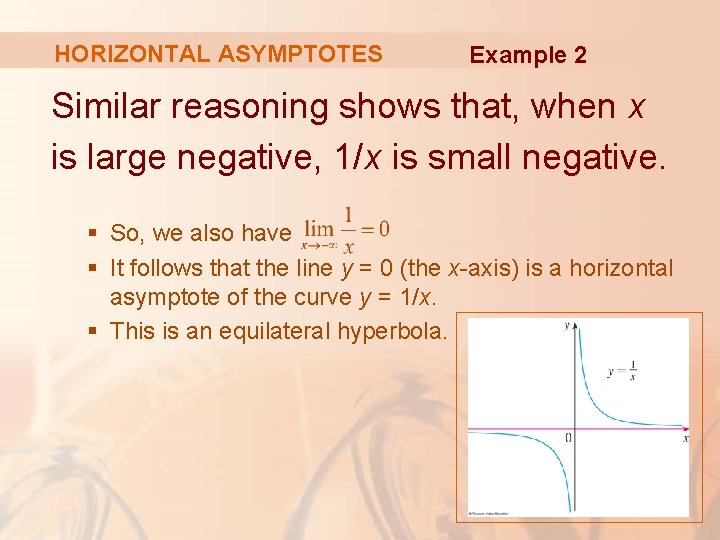
HORIZONTAL ASYMPTOTES Find Example 2 and § Observe that, when x is large, 1/x is small. § For instance, § In fact, by taking x large enough, we can make 1/x as close to 0 as we please. § Therefore, according to Definition 1, we have

HORIZONTAL ASYMPTOTES Example 2 Similar reasoning shows that, when x is large negative, 1/x is small negative. § So, we also have § It follows that the line y = 0 (the x-axis) is a horizontal asymptote of the curve y = 1/x. § This is an equilateral hyperbola.

HORIZONTAL ASYMPTOTES Most of the Limit Laws given in Section 2. 3 also hold for limits at infinity. § It can be proved that the Limit Laws (with the exception of Laws 9 and 10) are also valid if is replaced by or. § In particular, if we combine Laws 6 and 11 with the results of Example 2, we obtain the following important rule for calculating limits.

HORIZONTAL ASYMPTOTES 5. Theorem If r > 0 is a rational number, then If r > 0 is a rational number such that xr is defined for all x, then

HORIZONTAL ASYMPTOTES Example 3 Evaluate and indicate which properties of limits are used at each stage. § As x becomes large, both numerator and denominator become large. § So, it isn’t obvious what happens to their ratio. § We need to do some preliminary algebra.

HORIZONTAL ASYMPTOTES Example 3 To evaluate the limit at infinity of any rational function, we first divide both the numerator and denominator by the highest power of x that occurs in the denominator. § We may assume that in only large values of x. , since we are interested

HORIZONTAL ASYMPTOTES Example 3 In this case, the highest power of x in the denominator is x 2. So, we have:

HORIZONTAL ASYMPTOTES Example 3

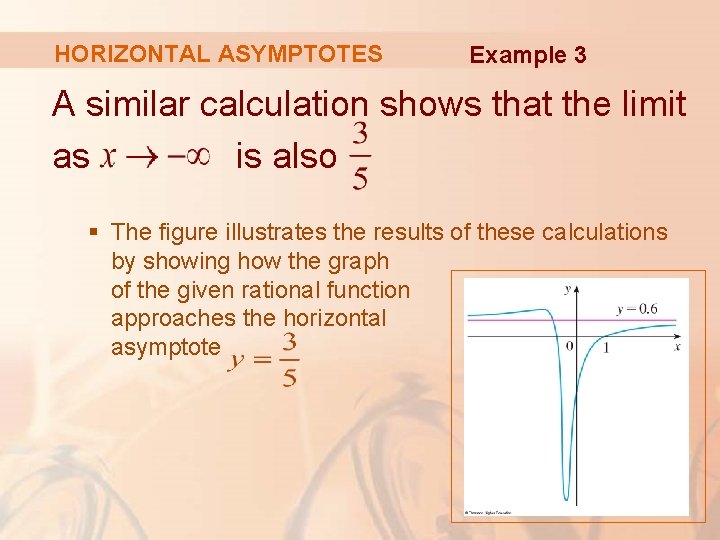
HORIZONTAL ASYMPTOTES Example 3 A similar calculation shows that the limit as is also § The figure illustrates the results of these calculations by showing how the graph of the given rational function approaches the horizontal asymptote

HORIZONTAL ASYMPTOTES Example 4 Find the horizontal and vertical asymptotes of the graph of the function

HORIZONTAL ASYMPTOTES Example 4 Dividing both numerator and denominator by x and using the properties of limits, we have:

HORIZONTAL ASYMPTOTES Example 4 Therefore, the line is a horizontal asymptote of the graph of f.

HORIZONTAL ASYMPTOTES Example 4 In computing the limit as , we must remember that, for x < 0, we have § So, when we divide the numerator by x, for x < 0, we get § Therefore,

HORIZONTAL ASYMPTOTES Example 4 Thus, the line is also a horizontal asymptote.

HORIZONTAL ASYMPTOTES Example 4 A vertical asymptote is likely to occur when the denominator, 3 x - 5, is 0, that is, when § If x is close to and , then the denominator is close to 0 and 3 x - 5 is positive. § The numerator is always positive, so f(x) is positive. § Therefore,

HORIZONTAL ASYMPTOTES Example 4 § If x is close to but , then 3 x – 5 < 0, so f(x) is large negative. § Thus, § The vertical asymptote is

HORIZONTAL ASYMPTOTES Example 5 Compute § As both and x are large when x is large, it’s difficult to see what happens to their difference. § So, we use algebra to rewrite the function.

HORIZONTAL ASYMPTOTES Example 5 We first multiply the numerator and denominator by the conjugate radical: § The Squeeze Theorem could be used to show that this limit is 0.

HORIZONTAL ASYMPTOTES Example 5 However, an easier method is to divide the numerator and denominator by x. § Doing this and using the Limit Laws, we obtain:

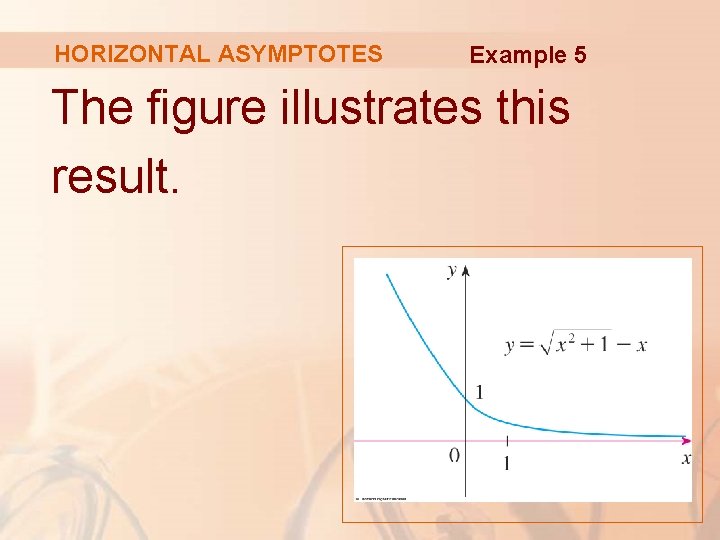
HORIZONTAL ASYMPTOTES Example 5 The figure illustrates this result.

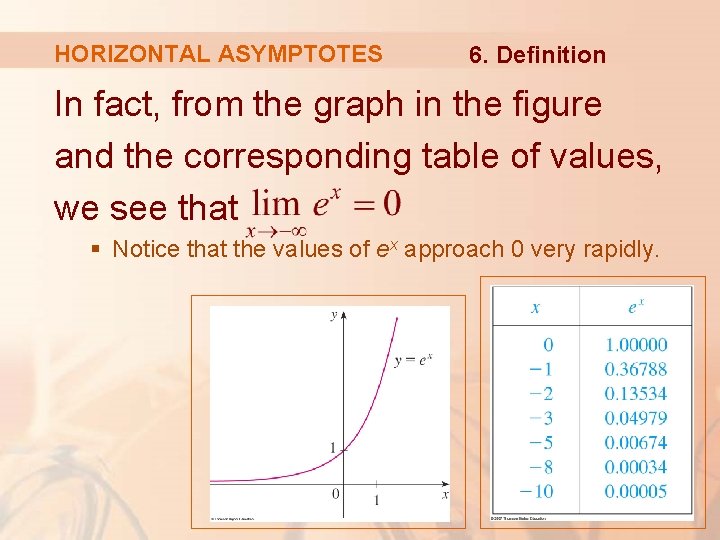
HORIZONTAL ASYMPTOTES The graph of the natural exponential function y = ex has the line y = 0 (the x-axis) as a horizontal asymptote. § The same is true of any exponential function with base a > 1.

HORIZONTAL ASYMPTOTES 6. Definition In fact, from the graph in the figure and the corresponding table of values, we see that § Notice that the values of ex approach 0 very rapidly.

HORIZONTAL ASYMPTOTES Example 6 Evaluate § If we let t = 1/x, we know that § Therefore, by (6), as

HORIZONTAL ASYMPTOTES Example 7 Evaluate § As x increases, the values of sin x oscillate between 1 and -1 infinitely often. § So, they don’t approach any definite number. § Thus, does not exist.

INFINITE LIMITS AT INFINITY The notation is used to indicate that the values of f(x) become large as x becomes large. § Similar meanings are attached to the following symbols:

INFINITE LIMITS AT INFINITY Find Example 8 and § When x becomes large, x 3 also becomes large. § For instance, § In fact, we can make x 3 as big as we like by taking x large enough. § Therefore, we can write

INFINITE LIMITS AT INFINITY Example 8 § Similarly, when x is large negative, so is x 3. § Thus, § These limit statements can also be seen from the graph of y = x 3 in the figure.

INFINITE LIMITS AT INFINITY Looking at the first figure, we see However, as the second figure demonstrates, y = ex becomes large as at a much faster rate than y = x 3.

INFINITE LIMITS AT INFINITY Example 9 Find § It would be wrong to write § The Limit Laws can’t be applied to infinite limits because is not a number ( can’t be defined). § However, we can write § This is because both x and x - 1 become arbitrarily large and so their product does too.

INFINITE LIMITS AT INFINITY Example 10 Find § As in Example 3, we divide the numerator and denominator by the highest power of x in the denominator, which is just x: because and as

INFINITE LIMITS AT INFINITY The next example shows that, by using infinite limits at infinity, together with intercepts, we can get a rough idea of the graph of a polynomial without having to plot a large number of points.

INFINITE LIMITS AT INFINITY Example 11 Sketch the graph of by finding its intercepts and its limits as and as § The y-intercept is f(0) = (-2)4(1)3(-1) = -16 § The x-intercepts are found by setting y = 0: x = 2, -1, 1.

INFINITE LIMITS AT INFINITY Example 11 Notice that, since (x - 2)4 is positive, the function doesn’t change sign at 2. Thus, the graph doesn’t cross the x-axis at 2. § It crosses the axis at -1 and 1.

INFINITE LIMITS AT INFINITY Example 11 When x is large positive, all three factors are large, so When x is large negative, the first factor is large positive and the second and third factors are both large negative, so

INFINITE LIMITS AT INFINITY Example 11 Combining this information, we give a rough sketch of the graph in the figure.

PRECISE DEFINITIONS 7. Definition 1 can be stated precisely as follows. Let f be a function defined on some interval (a, ). Then, means that, for every , there is a corresponding number N such that if x > N, then

PRECISE DEFINITIONS In words, this says that the values of f(x) can be made arbitrarily close to L (within a distance , where is any positive number) by taking x sufficiently large (larger than N, where N depends on ).

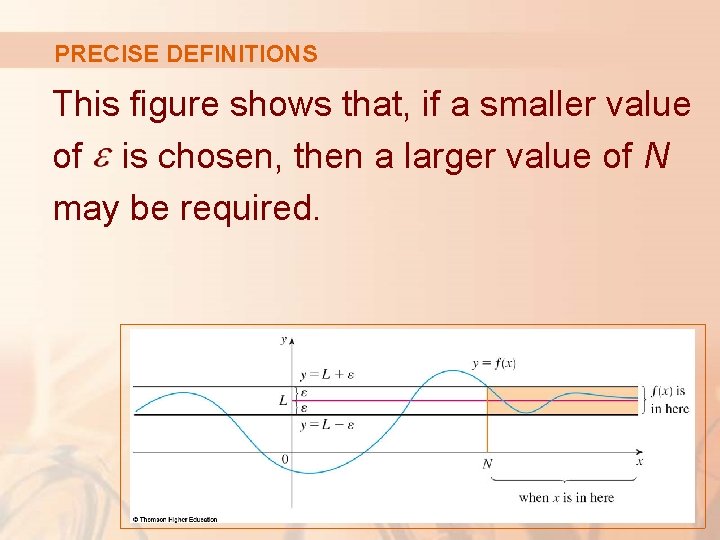
PRECISE DEFINITIONS Graphically, it says that, by choosing x large enough (larger than some number N), we can make the graph of f lie between the given horizontal lines and § This must be true no matter how small we choose.

PRECISE DEFINITIONS This figure shows that, if a smaller value of is chosen, then a larger value of N may be required.

PRECISE DEFINITIONS 8. Definition Similarly, a precise version of Definition 2 is given as follows. Let f be a function defined on some interval ( , a). Then, means that, for every , there is a corresponding number N such that, if x < N, then

PRECISE DEFINITIONS This is illustrated in the figure.

PRECISE DEFINITIONS In Example 3, we calculated that In the next example, we use a graphing device to relate this statement to Definition 7 with and
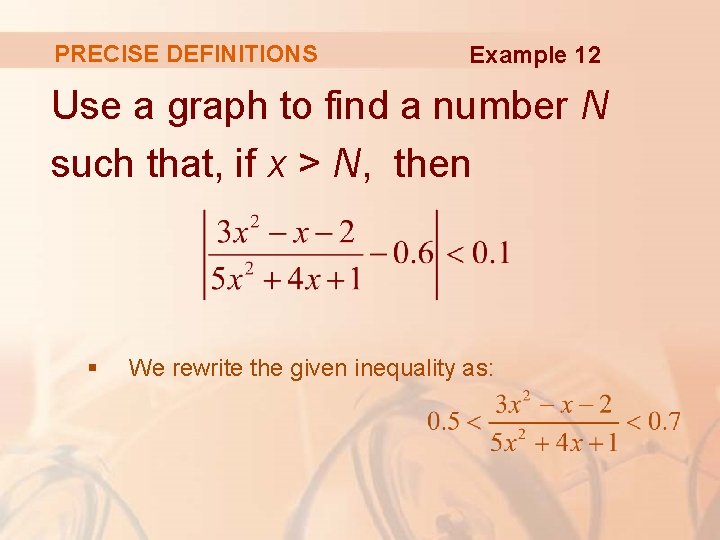
PRECISE DEFINITIONS Example 12 Use a graph to find a number N such that, if x > N, then § We rewrite the given inequality as:

PRECISE DEFINITIONS Example 12 We need to determine the values of x for which the given curve lies between the horizontal lines y = 0. 5 and y = 0. 7 § So, we graph the curve and these lines in the figure.

PRECISE DEFINITIONS Example 12 Then, we use the cursor to estimate that the curve crosses the line y = 0. 5 when § To the right of this number, the curve stays between the lines y = 0. 5 and y = 0. 7

PRECISE DEFINITIONS Example 12 Rounding to be safe, we can say that, if x > 7, then § In other words, for , we can choose N = 7 (or any larger number) in Definition 7.

PRECISE DEFINITIONS Example 13 Use Definition 7 to prove § Given , we want to find N such that, if x > N, then § In computing the limit, we may assume that x > 0 § Then,

PRECISE DEFINITIONS Example 13 Let’s choose So, if , then Therefore, by Definition 7,

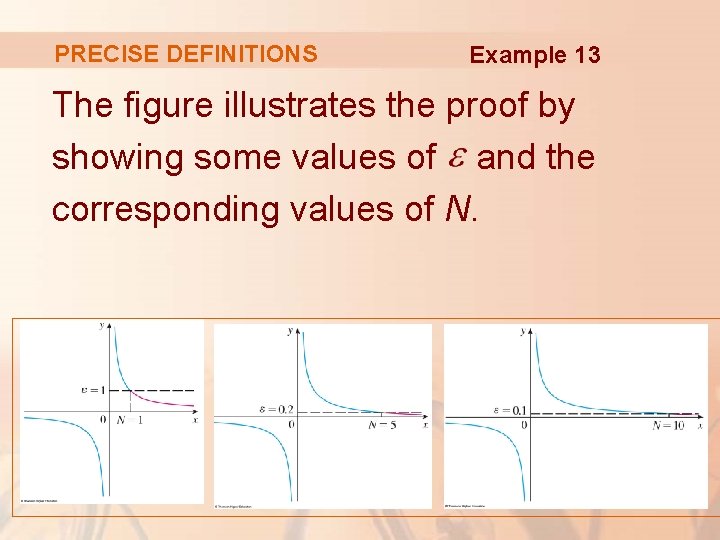
PRECISE DEFINITIONS Example 13 The figure illustrates the proof by showing some values of and the corresponding values of N.

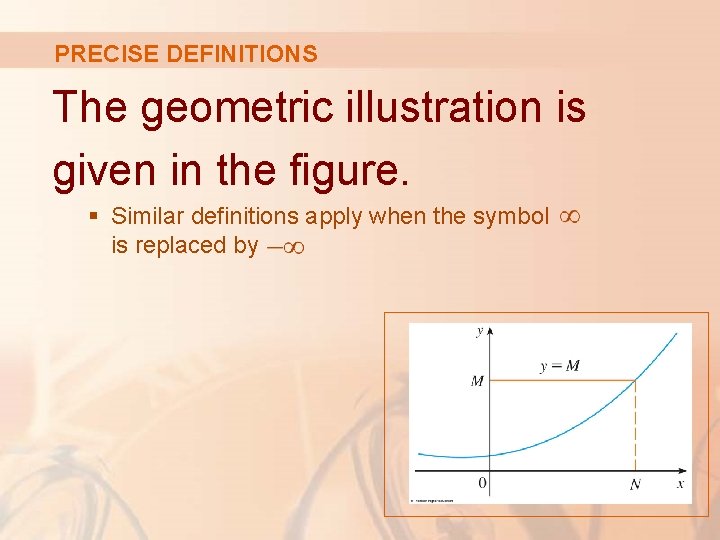
PRECISE DEFINITIONS 9. Definition Finally, we note that an infinite limit at infinity can be defined as follows. Let f be a function defined on some interval (a, ). Then, means that, for every positive number M, there is a corresponding positive number N such that, if x > N, then f(x) > M

PRECISE DEFINITIONS The geometric illustration is given in the figure. § Similar definitions apply when the symbol is replaced by
 Ncert limits and derivatives pdf
Ncert limits and derivatives pdf Limits and derivatives
Limits and derivatives Limits and derivatives
Limits and derivatives Limits involving infinity
Limits involving infinity Real limits statistics
Real limits statistics Product and quotient rules and higher order derivatives
Product and quotient rules and higher order derivatives Brown sauce derivatives
Brown sauce derivatives Stomodeum
Stomodeum Fed tapering
Fed tapering Exponential derivative
Exponential derivative Derivative of inverse function
Derivative of inverse function Constant multiple theorem
Constant multiple theorem Carboxylic acid derivatives
Carboxylic acid derivatives Advantages and disadvantages of derivatives
Advantages and disadvantages of derivatives Carboxylic acid to ester
Carboxylic acid to ester How to name carboxylic acid
How to name carboxylic acid Nucleophilic substitution of carboxylic acids
Nucleophilic substitution of carboxylic acids Leading sauce
Leading sauce Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Derivatives and the shape of a graph
Derivatives and the shape of a graph Options futures and other derivatives
Options futures and other derivatives Acylation of benzene
Acylation of benzene Mother sauces and derivatives
Mother sauces and derivatives Derivatives of cosine
Derivatives of cosine Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Limit and continuity solved problems
Limit and continuity solved problems Limits fits and tolerances lecture notes
Limits fits and tolerances lecture notes Radiation dose limits for workers and public pdf
Radiation dose limits for workers and public pdf Calculus chapter 2 limits and continuity
Calculus chapter 2 limits and continuity Limit fit tolerance
Limit fit tolerance Limits and their properties
Limits and their properties Limits and their properties
Limits and their properties Fits and tolerances chart
Fits and tolerances chart Thomas calculus limits and continuity
Thomas calculus limits and continuity Plasticity index chart of soil
Plasticity index chart of soil Understanding limits graphically and numerically
Understanding limits graphically and numerically Finding limits graphically and numerically
Finding limits graphically and numerically Find limit
Find limit Limits at infinity (horizontal asymptotes)
Limits at infinity (horizontal asymptotes) Estimating limits graphically
Estimating limits graphically Limit and continuity solved problems
Limit and continuity solved problems Evaluating limits graphically
Evaluating limits graphically Limits and continuity
Limits and continuity Lesson 2 understanding limits graphically and numerically
Lesson 2 understanding limits graphically and numerically Chapter 1 limits and their properties
Chapter 1 limits and their properties Trig limits
Trig limits Application of limits and continuity
Application of limits and continuity Chapter 1 limits alternatives and choices
Chapter 1 limits alternatives and choices Vertical and horizontal asymptotes limits
Vertical and horizontal asymptotes limits Lateral lingual swellings
Lateral lingual swellings Algebraic differentiation
Algebraic differentiation Implicit derivative
Implicit derivative Find y
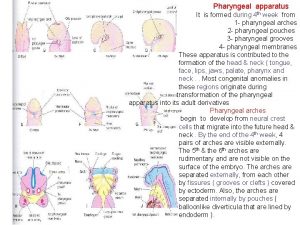
Find y Pharyngeal arches
Pharyngeal arches Least reactive carboxylic acid derivatives
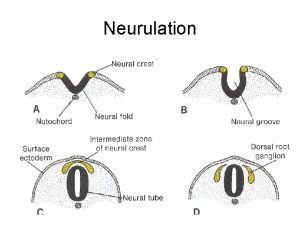
Least reactive carboxylic acid derivatives Neurulation
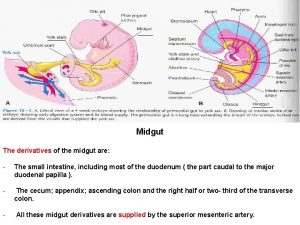
Neurulation Derivatives of mid gut
Derivatives of mid gut Find y'' if x^4+y^4=16
Find y'' if x^4+y^4=16 Urushiol is a hydroxy derivative of phenol
Urushiol is a hydroxy derivative of phenol Mesoderm derivatives
Mesoderm derivatives Higher order derivatives definition
Higher order derivatives definition Mesoderm derivatives
Mesoderm derivatives Development of superior vena cava
Development of superior vena cava Veins
Veins Derivatives week
Derivatives week Blue-chip indices
Blue-chip indices Constant multiple theorem
Constant multiple theorem Warp rib
Warp rib Derivatives 2
Derivatives 2 Derivatives asset class
Derivatives asset class Hyperbolic functions derivatives
Hyperbolic functions derivatives Derivatives of unequally spaced data
Derivatives of unequally spaced data Diazomethane reaction with carboxylic acid
Diazomethane reaction with carboxylic acid Coarcotation
Coarcotation Bilaminar
Bilaminar